Методы расчета КИХ-фильтров

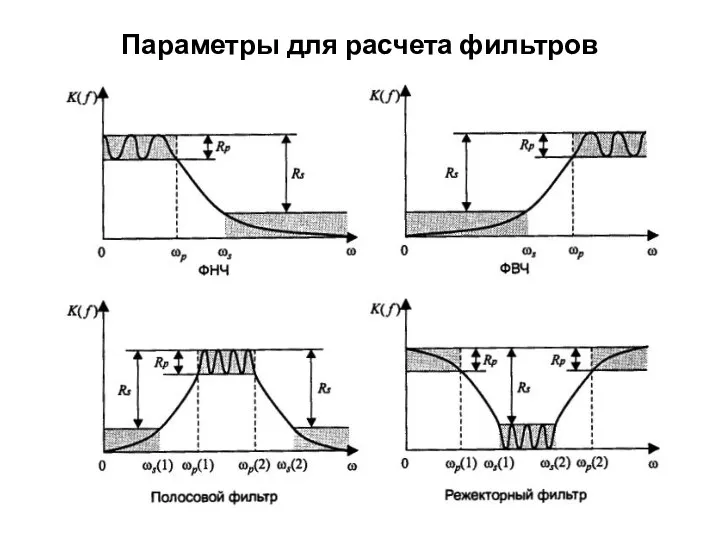
Параметры для расчета фильтров

Нерекурсивные фильтры

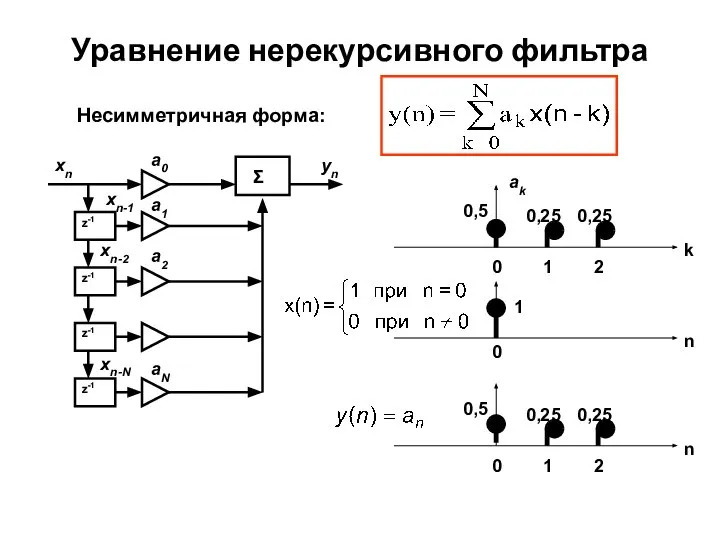
Уравнение нерекурсивного фильтра
Несимметричная форма:
xn
a0
a1
a2
aN
xn-1
xn-2
xn-N
Σ
yn

Уравнение нерекурсивного фильтра
Cимметричная форма:
Пример: N=2
будущие выборки
Cимметричная форма записи адекватна обработке записанных сигналов

Частотная характеристика нерекурсивного фильтра
Воздействие – комплексная гармоника:
Отклик:
Частотная характеристика:
Четность-нечетность
коэффициентов:

Частотная характеристика нерекурсивного фильтра
ЧХ цифрового фильтра периодична:
Коэффициенты:

Расчет фильтра

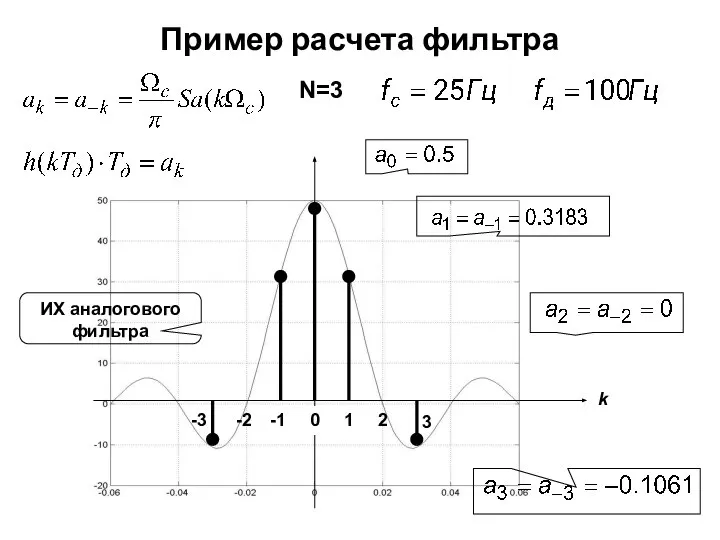
Пример расчета фильтра
N=3
k
0
1
2
3
-1
-2
-3
ИХ аналогового фильтра

Расчет фильтра в Matlab
% === freq_har.m === Частотная хар-ка ФНЧ ===
a0=0.5; % нулевой коэффициент фильтра
ak=[0.3183 0 -0.1061]; % коэффициенты фильтра c 1 по 3
fd=100; % частота дискретизацации
dt=1/fd; % период (шаг) дискретизации
N=3; % половина порядка фильтра
df=0.02*fd; % шаг по частоте
f=-0.5*fd:df:1.5*fd; % диапазон частот
% === расчет суммы ===
sum=0;
for k=1:N,
sum=sum+ak(k)*cos(2*pi*f*k*dt);
end;
H=a0+2*sum; % частотная хар-ка
plot(f,H) % построение графика
grid on % построение сетки

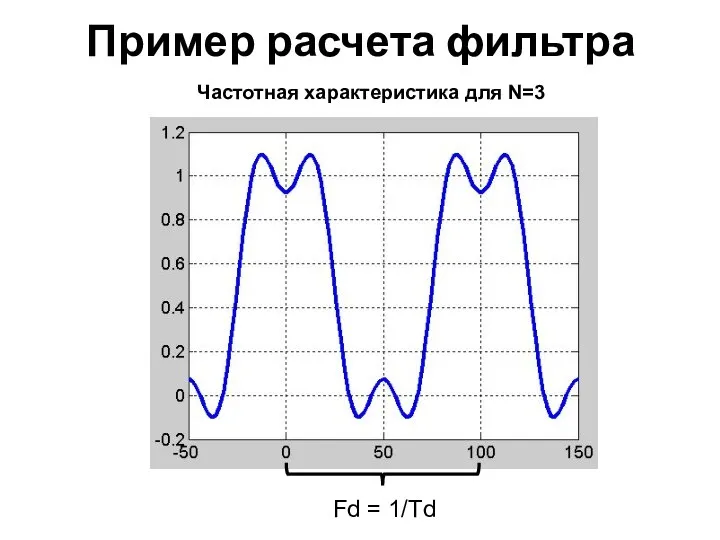
Пример расчета фильтра
Частотная характеристика для N=3
Fd = 1/Td

Окна в цифровых фильтрах
Прямоугольное (Дирихле)
Треугольное (Бартлетта)
Хэннинга (Ханна)
Хэмминга
Блэкмана
Ланцоша

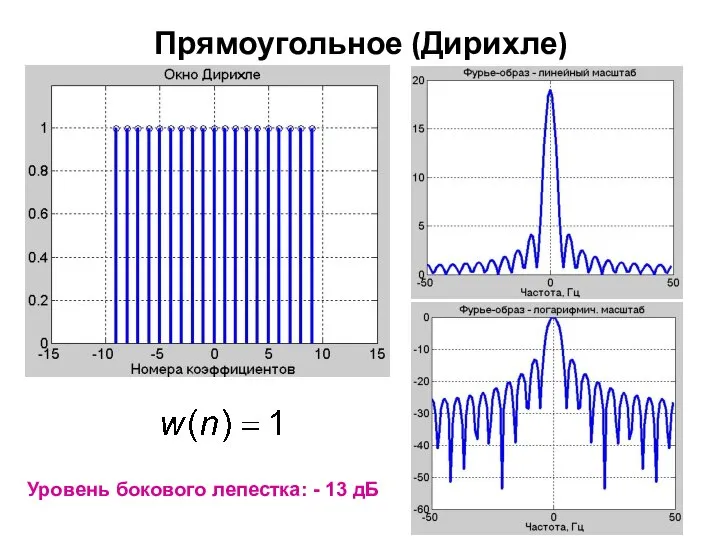
Прямоугольное (Дирихле)
Уровень бокового лепестка: - 13 дБ

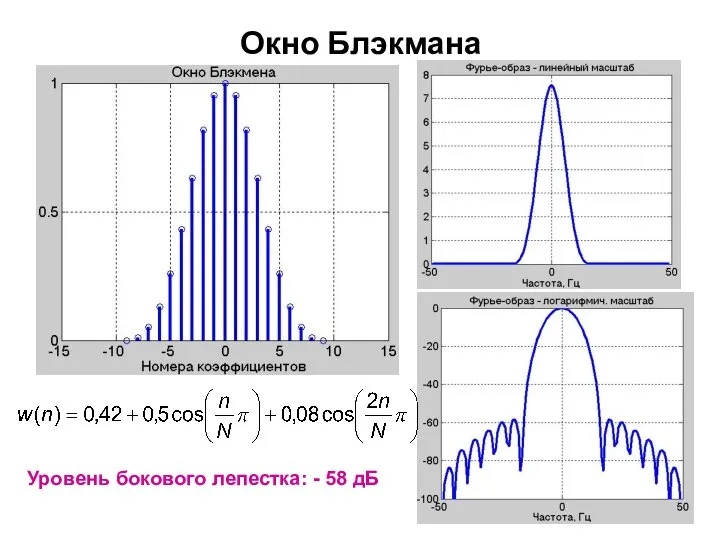
Окно Блэкмана
Уровень бокового лепестка: - 58 дБ

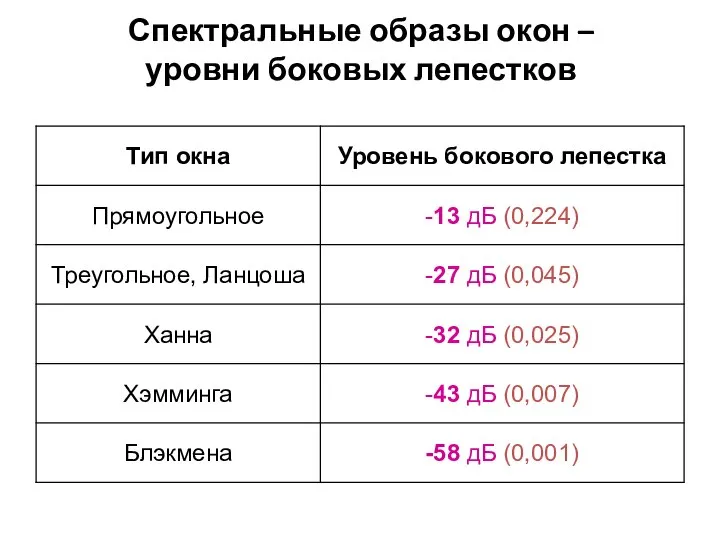
Спектральные образы окон –
уровни боковых лепестков

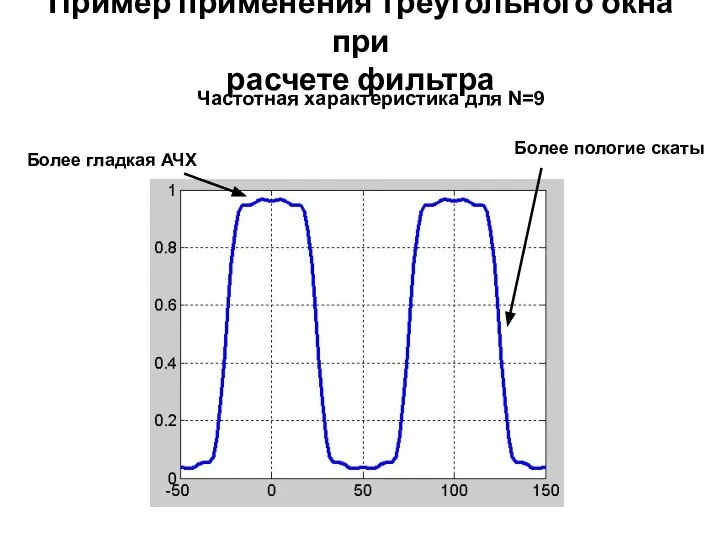
Пример применения треугольного окна при
расчете фильтра
Частотная характеристика для N=9
Более пологие скаты
Более гладкая АЧХ

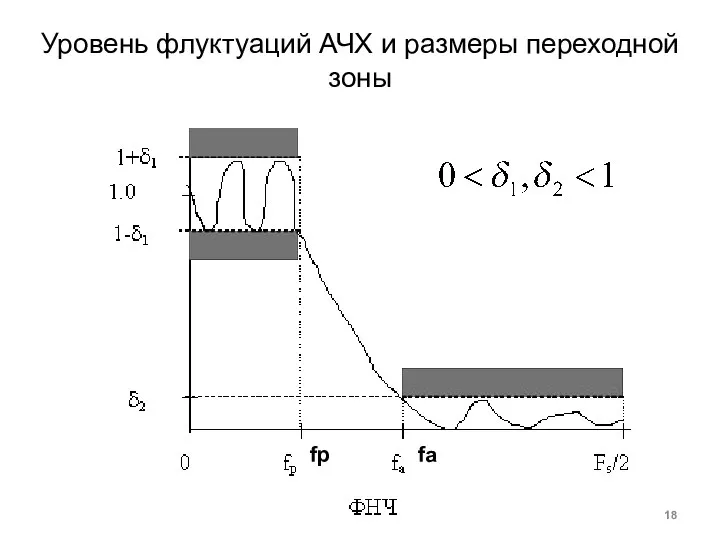
Методика Кайзера расчета фильтра
Выбирают значение параметра «альфа», исходя из уровня флуктуаций АЧХ
Вычисляют порядок фильтра, исходя из:
- уровня флуктуаций АЧХ;
- размеров переходной зоны.
Вычисляют коэффициенты ak методом обратного преобразования Фурье

Уровень флуктуаций АЧХ и размеры переходной зоны
fp
fa

Расчет параметра «альфа»

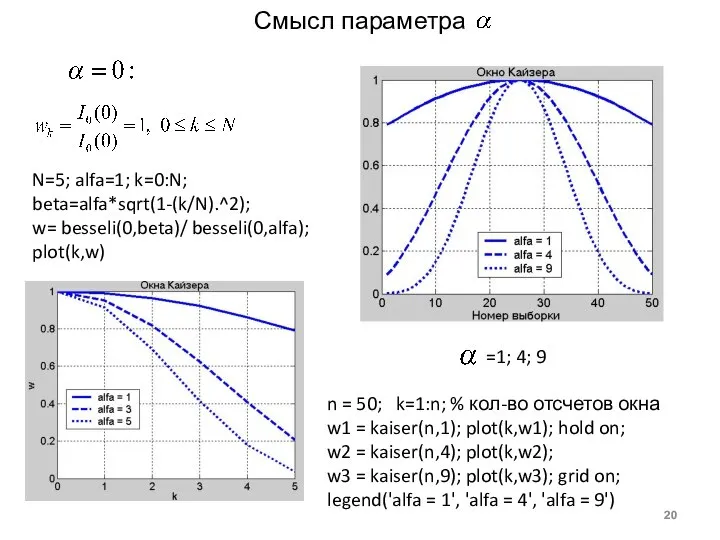
Смысл параметра
n = 50; k=1:n; % кол-во отсчетов окна
w1 = kaiser(n,1); plot(k,w1); hold on;
w2 = kaiser(n,4); plot(k,w2);
w3 = kaiser(n,9); plot(k,w3); grid on;
legend('alfa = 1', 'alfa = 4', 'alfa = 9')
=1; 4; 9
N=5; alfa=1; k=0:N;
beta=alfa*sqrt(1-(k/N).^2);
w= besseli(0,beta)/ besseli(0,alfa);
plot(k,w)

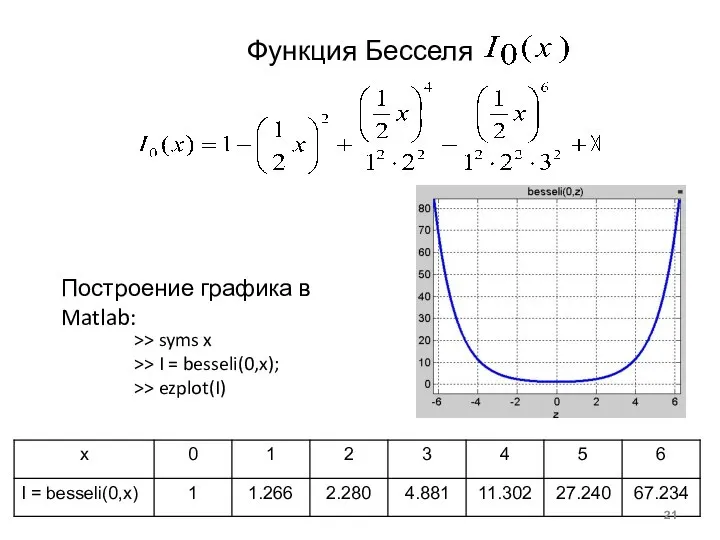
Функция Бесселя
>> syms x
>> I = besseli(0,x);
>> ezplot(I)
Построение графика в Matlab:

Расчет КИХ-фильтров с окном Кайзера
- функция Бесселя первого рода нулевого порядка
- специальный числовой параметр окна Кайзера

АЧХ окна Кайзера
% W1 – Фурье-образ окна Кайзера
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs(W1))); hold on;
plot(f, 20*log10(abs(W2)), 'g');
plot(f, 20*log10(abs(W3)), 'r');
legend('a=1', 'a=4', 'a=9')
grid on
С ростом параметра «альфа»
изменяются АЧХ окна Кайзера:
уменьшается уровень боковых лепестков,
расширяется главный лепесток
Уровень боковых лепестков

Размеры переходной зоны
ФНЧ:
ФВЧ:
ПФ:
РФ:

Расчет минимального порядка фильтра
Учет уровня флуктуаций
Учет размеров переходной зоны

Расчеты по методике Кайзера в среде Matlab
Вычисление параметров окна Кайзера:
[p, Wn, alfa, ftype] = kaiserord(fcuts, mags, devs, Fs)
в полосе от нуля до fcuts(1) АЧХ равна mags(1),
в полосе от fcuts(2) до fcuts(3) АЧХ равна mags(2), … ,
в полосе от fcuts(end) до Fs/2 АЧХ равна mags(end)
Вычисление отсчетов окна Кайзера:
w = kaiser(p+1,alfa)
Параметр devs д.б. вектором той же длины, что и mags
Вычисление коэфф-в КИХ-фильтра с окном Кайзера:
a = fir1(p, Wn, ftype, kaiser(p+1, alfa), ‘noscale’)
Проверка расчетов путем построения АЧХ
freqz(a, 1, 512, Fs);

Fs = 100;
fcuts = [25 33];
mags = [1 0];
devs = [0.05 0.01];
[p,Wn,alfa,ftype] = kaiserord(fcuts,mags,devs,Fs);
a = fir1(p,Wn,ftype,kaiser(p+1,alfa),'noscale');
freqz(a, 1, 512, Fs)
Пример:
Расчеты по методике Кайзера в среде Matlab
p = 28

Синтез оптимальных
(по Чебышеву) КИХ-фильтров

Недостатки оконного метода:
Уменьшение крутизны АЧХ в переходной зоне
Трудно прогнозировать форму АЧХ фильтра
Теоретическое обоснование
Синтез фильтров, оптимальных по Чебышеву –
задача оптимальной аппроксимации H(w):
Задаются:
Граничные частоты;
Величина предельно допустимых флуктуаций
- наилучшее равномерное приближение

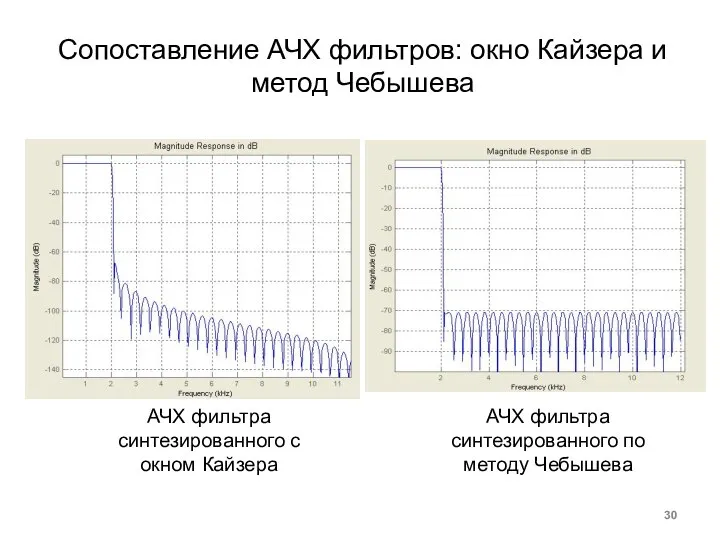
Сопоставление АЧХ фильтров: окно Кайзера и метод Чебышева

Для наилучшего равномерного приближения функции
полиномом необходимо и достаточно, чтобы равенство
Теорема Чебышева об альтернансе
Тригонометрический полином:
выполнялось не менее чем в N+2 точках (точках альтернанса),
принадлежащих интервалам аппроксимации,
причем знак разности чередуется от точки к точке

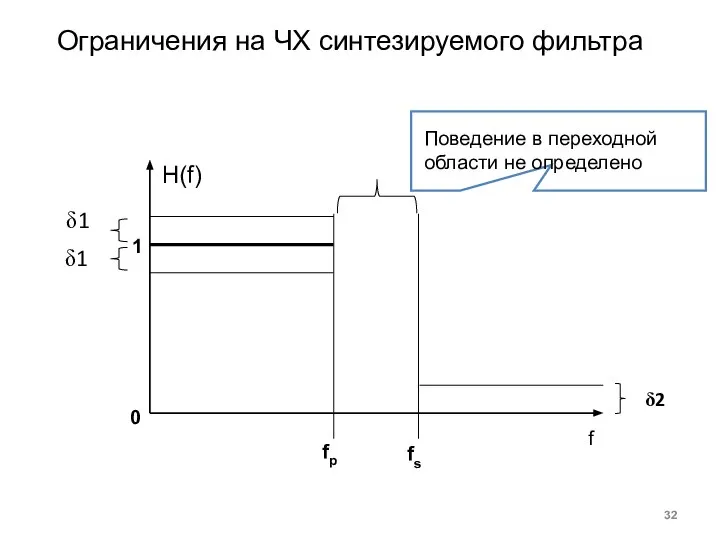
Ограничения на ЧХ синтезируемого фильтра
Поведение в переходной
области не определено
1
δ1
δ2
fр
fs
0
H(f)
f
δ1

Алгоритм Ремеза (Е.Я. Ремез - украинский академик (1896-1975) )
- частоты альтернанса;
Составляется и решается система N+2 уравнений:
Поскольку частоты альтернанса неизвестны:
на первой итерации они задаются приблизительно;
на последующих итерациях они уточняются.
Недостаток метода – может потребоваться много итераций
- искомые коэффициенты.

Компьютерная реализация алгоритма Ремеза в Matlab
Parks, McClellan
определяют минимальный порядок фильтра n:
[n, f0, a0, w] = remezord(f, A, dev, Fs)
параметры f, A совместно задают кусочно-постоянную АЧХ
в зонах пропускания и задержания
2) вычисляют коэффициенты фильтра:
а = remez(n, f0, а0, w)
remezord
firpmord
remez
firpm
вспомогательные параметры
В последних версиях Matlab:
Remez

Пример: синтез НЧ фильтра с граничными частотами 500 Гц и 600 Гц, частотой дискретизации 2 кГц
Rp = 3; % Неравномерн. в полосе пропуск. (в дБ)
Rs = 40; % Неравномерн. в полосе задерж. (в дБ)
Fs = 2000; % Частота дискретизации
f = [500 600]; % Границы переходной зоны
A = [1 0]; % Желаемые значения АЧХ
% Расчет девиаций
dev = [(10^(Rp/20)-1)/(10^(Rp/20)+1) 10^(-Rs/20)];
[n, fo, ao, w] = remezord(f, A, dev, Fs);
a = remez(n, fo, ao, w);
freqz(a, 1, 1024, Fs);
title('Lowpass Filter Designed to Specifications');

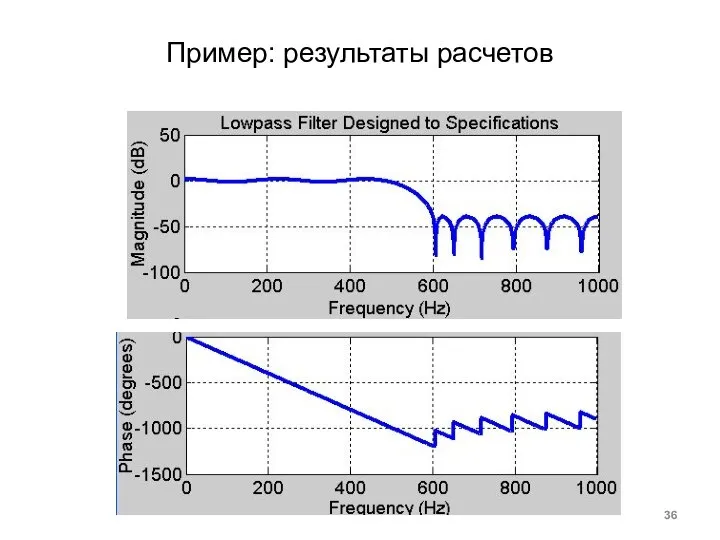
Пример: результаты расчетов