Содержание
- 2. Слово «тригонометрия» впервые встречается в 1505г в заглавии книги немецкого теолога и математика Питискуса. Происходит от
- 3. Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде,
- 4. Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила
- 5. В 8 в. Учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов
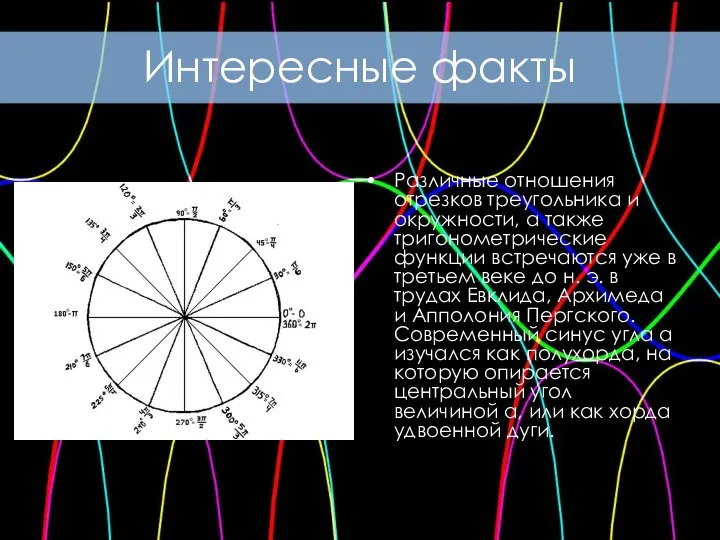
- 6. Различные отношения отрезков треугольника и окружности, а также тригонометрические функции встречаются уже в третьем веке до
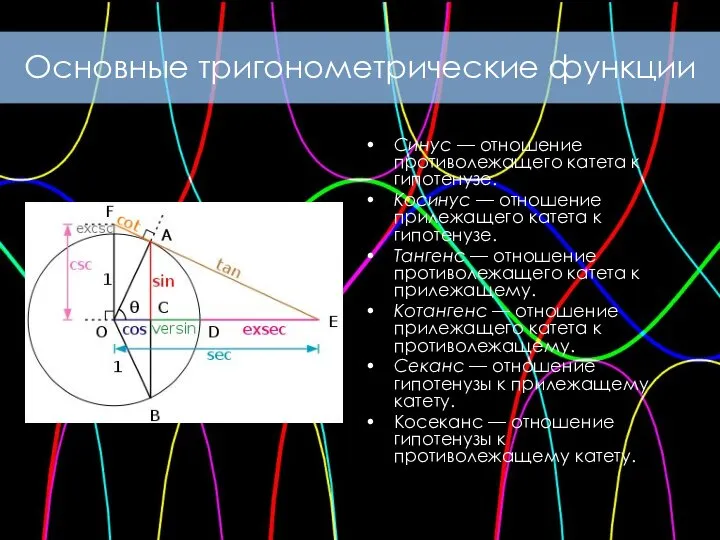
- 7. Основные тригонометрические функции Синус — отношение противолежащего катета к гипотенузе. Косинус — отношение прилежащего катета к
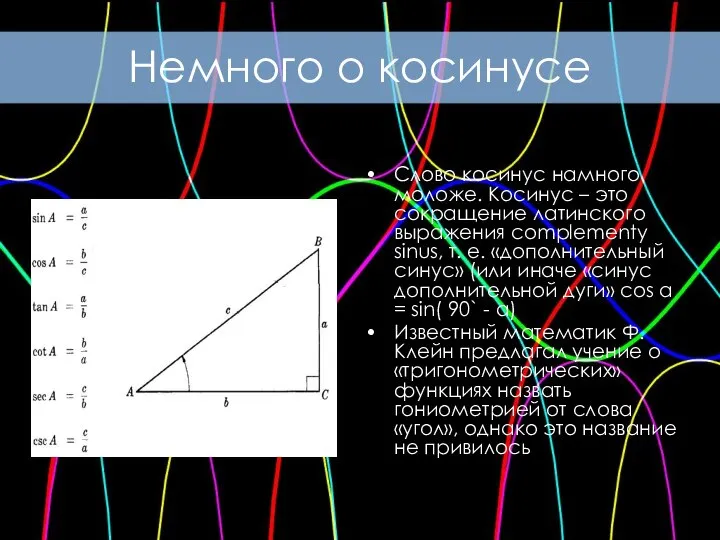
- 8. Слово косинус намного моложе. Косинус – это сокращение латинского выражения complementy sinus, т. е. «дополнительный синус»
- 9. Современный вид тригонометрии придал крупнейший математик восемнадцатого столетия Л. Эйлер. Он ввел известные определения тригонометрических функций,
- 10. Где тригонометрия нашла применение? Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.
- 11. Применение тригонометрии Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ
- 13. Скачать презентацию






 Нулевой угловой коэффицент
Нулевой угловой коэффицент В стране математики
В стране математики Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Площади. Формула Пика
Площади. Формула Пика Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Первые уроки в 5 кассе
Первые уроки в 5 кассе Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Таблица сложения
Таблица сложения Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Элементы теории вероятности
Элементы теории вероятности График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Иррациональные уравнения
Иррациональные уравнения Смежные углы
Смежные углы Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени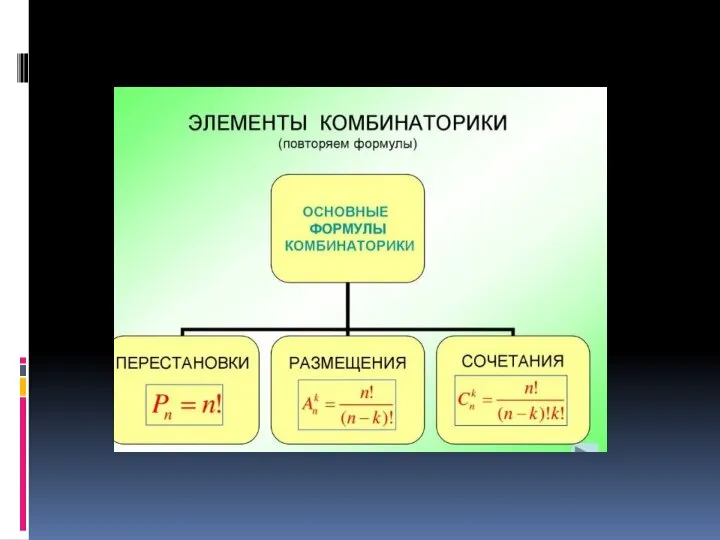 Основные понятия комбинаторики
Основные понятия комбинаторики Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс) 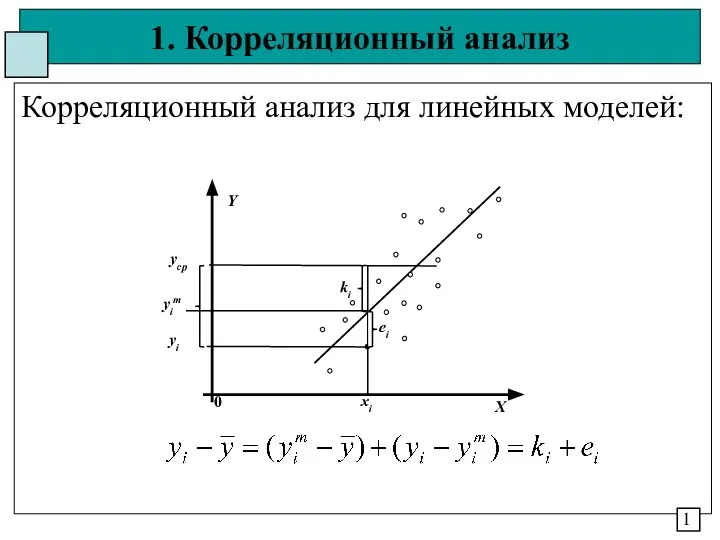 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Решение тригонометрических уравнений
Решение тригонометрических уравнений Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Спиннеры и метематика
Спиннеры и метематика krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Обратные матрицы
Обратные матрицы Сравнение моделей
Сравнение моделей Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс)  Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве