Многогранники и тела с кривыми поверхностями

1. Пирамида - это многогранник, одна грань которого - многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью

2. Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом

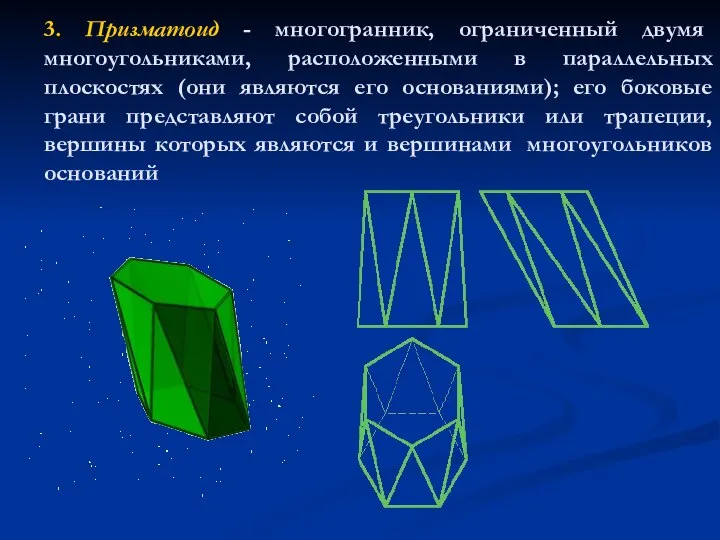
3. Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований

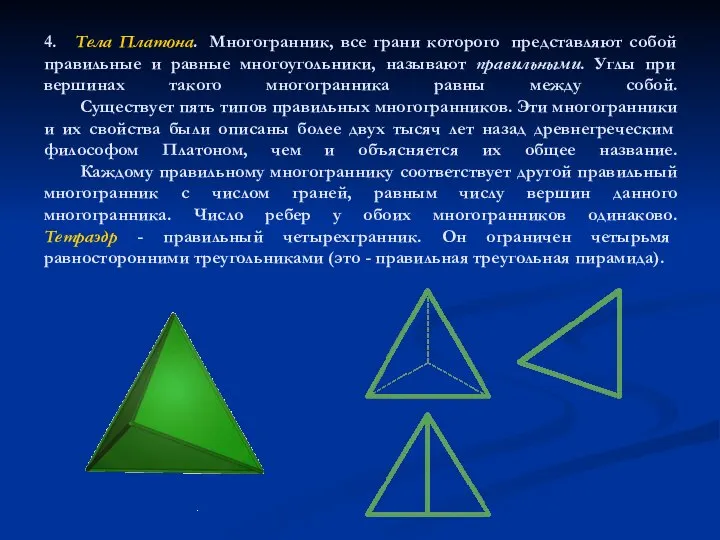
4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).

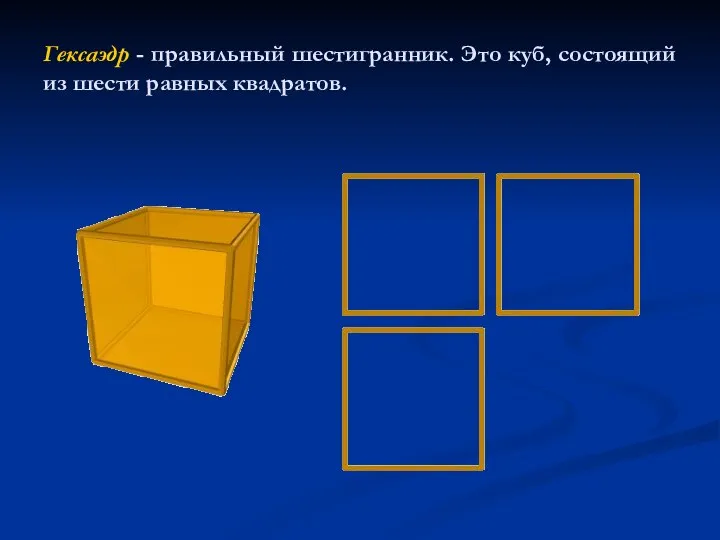
Гексаэдр - правильный шестигранник. Это куб, состоящий из шести равных квадратов.

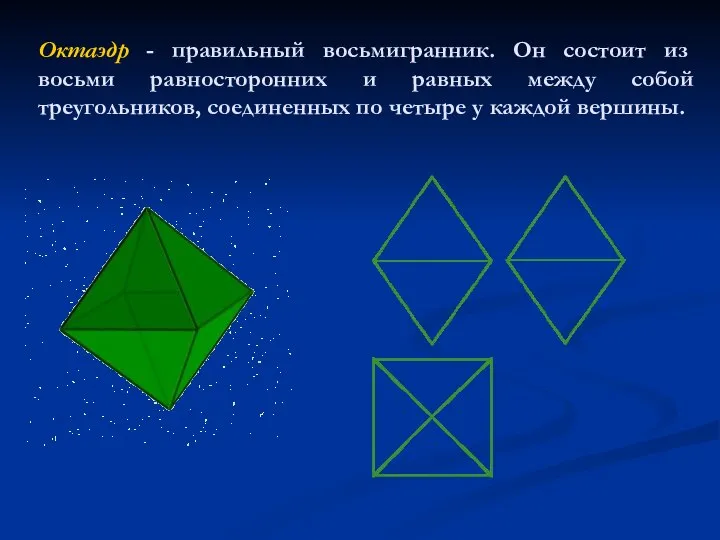
Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

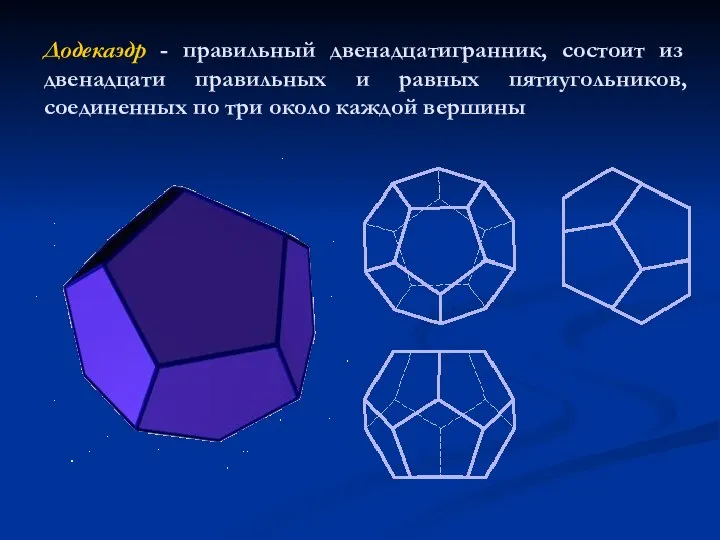
Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины

Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины

5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.
Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.

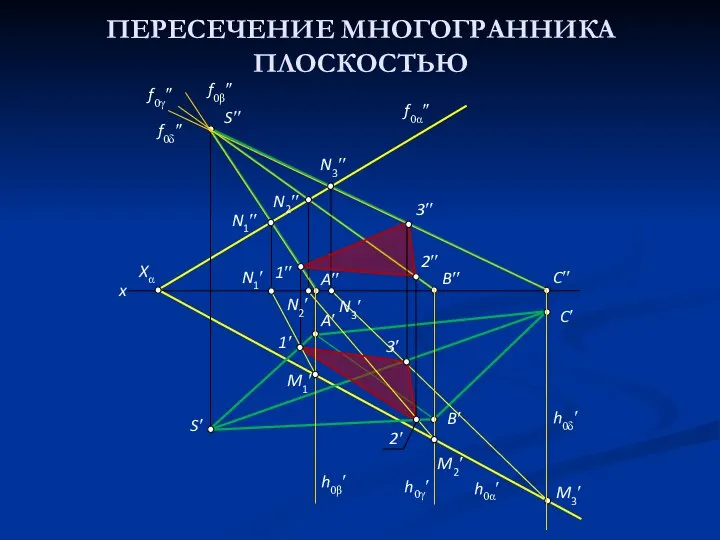
ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
Сечение многогранника плоскостью представляет собой плоскую замкнутую ломаную линию.
Построение сечения можно провести двумя способами:
способом «граней» – найти линии пересечения граней с заданной плоскостью;
способом «ребер» – найти точки встречи ребер пирамиды с плоскостью и последовательно соединить их.

ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
M2′
M3′
2′
M1′
N3′′
N2′′
h0β′
h0γ′
h0δ′
3′
1′
N3′
N2′
N1′
2′′
1′′
N1′′
3′′
f0δ″
f0β″
f0γ″

ПЕРЕСЕЧЕНИЕ КОНУСА И ЦИЛИНДРА ПЛОСКОСТЬЮ
Для построения сечения конуса или цилиндра плоскостью в нее необходимо вписать многогранник (соответственно пирамиду или призму), построить сечение вписанного многогранника плоскостью, а затем полученные на ребрах многогранника точки соединить плавной кривой линией по лекалу.
В результате получим приближенное решение задачи, точность которого будет определяться числом граней вписанного многогранника.

ПЕРЕСЕЧЕНИЕ КОНУСА И ЦИЛИНДРА ПЛОСКОСТЬЮ
2′′
5′′
3′′
5′
4′
M2′
M1′
M3′
1′
2′
N2′
N1′
N1′′
N2′′
N3′′
f0β′′
f0γ′′
f0ε′′
N3′
3′
1′′
4′′
A′′
B′′≡F′′
C′′≡E′′
D′′
h0β′
h0γ′
h0ε′

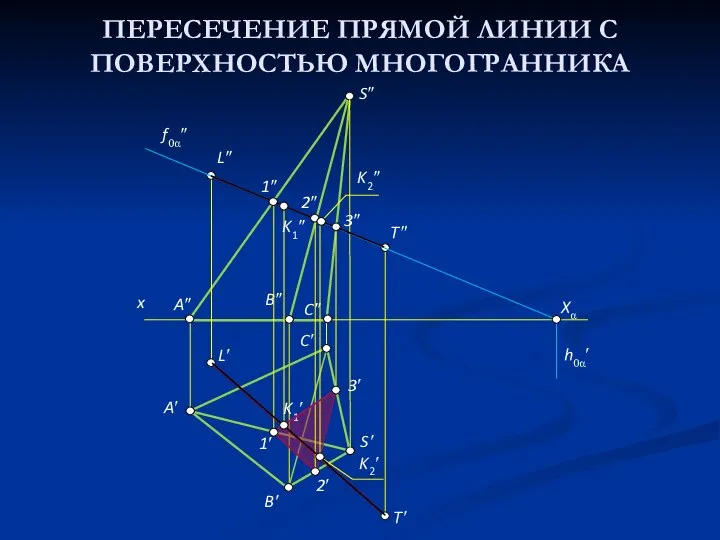
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА
Для построения точек пересечения прямой линии с поверхностью многогранника необходимо:
1) через прямую провести любую вспомогательную плоскость;
2) построить сечение многогранника этой вспомогательной плоскостью;
3) найти искомые точки в пересечении прямой с контурами построенного сечения.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА
K1′
3′
K2″
K1″
3″
f0α″
h0α′
Xα
1″
2″
1′
2′
K2′

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ КОНУСА И ЦИЛИНДРА
Точки пересечения прямой линии с поверхностью конуса или цилиндра можно построить двумя способами.
Первый способ заключается в том, что в конус или цилиндр вписывают соответственно пирамиду или призму, строят сечение вписанного многогранника вспомогательной плоскостью и полученные точки на ребрах соединяют плавной кривой. Точки пересечения прямой с построенным сечением есть точки пересечения этой прямой с поверхностью заданного геометрического тела. В результате получаем приближенное решение задачи.
Для получения точного решения вспомогательную плоскость нужно выбрать так, чтобы полученное сечение линейчатой поверхности представляло собой простейшую фигуру – многоугольник. В случае конической поверхности такая плоскость должна проходить через заданную прямую и вершину конуса, тогда в сечении образуется
треугольник.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ КОНУСА
K2′
K1′
2′
К2′′
h0α′
К1′′
M1′
M2′′
M1′′
M2′
1′

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ ЦИЛИНДРА
Для получения точного решения в качестве вспомогательной плоскости выбираем плоскость общего положения, параллельную оси цилиндра, и задаем ее двумя пересекающимися прямыми – прямой LT и произвольной прямой, параллельной оси. Такую прямую можно провести через любую точку прямой LT. Горизонтальная проекция прямой параллельна О1′О2′, а фронтальная проекция – О1′′О2′′.
Поскольку вспомогательная плоскость выбрана параллельной оси цилиндра, сечение будет представлять собой
параллелограмм.