Содержание
- 2. «Каждая решённая мною задача становилась образцом, который служил впоследствии для решения других задач»
- 3. Задача 1. В прямоугольнике ABCD опущен перпендикуляр BK на диагональ AC. Точки M и N –
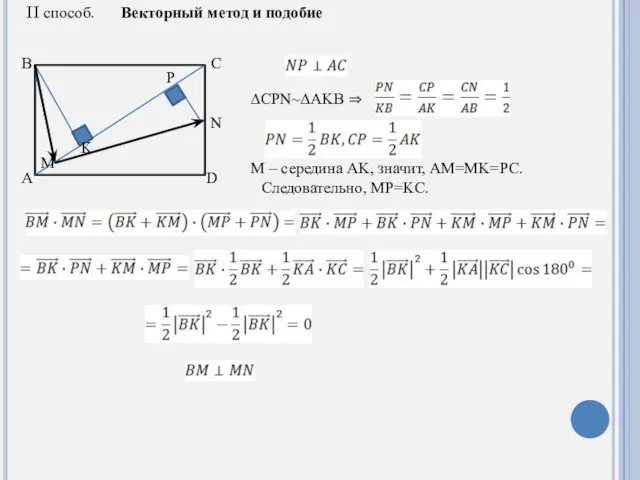
- 4. A B C M N K D II способ. Векторный метод и подобие P ∆CPN~∆AKB ⇒
- 5. A B C M N K D P III способ Применение тригонометрии Убедимся, что Пусть ∠ACB
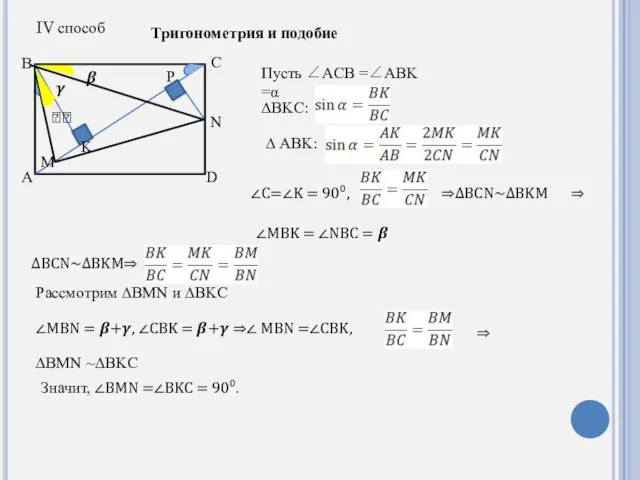
- 6. A B C M N K D P IV способ Тригонометрия и подобие Пусть ∠ACB =∠ABK
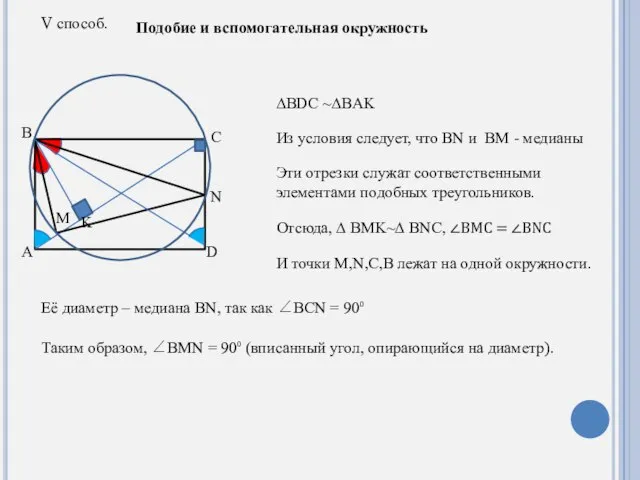
- 7. V способ. Подобие и вспомогательная окружность A B C M N K D ∆BDC ~∆BAK Из
- 8. VI способ. Обратный ход A B C M K D P Предположим, что ∠BMN - прямой,
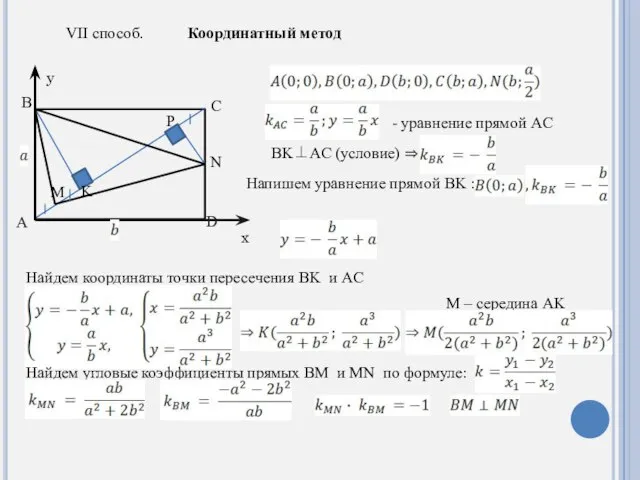
- 9. VII способ. Координатный метод A B C M K D P N x y - уравнение
- 10. Задача №2 Точка E – середина стороны AD параллелограмма ABCD, прямые BE и AC взаимно перпендикулярны
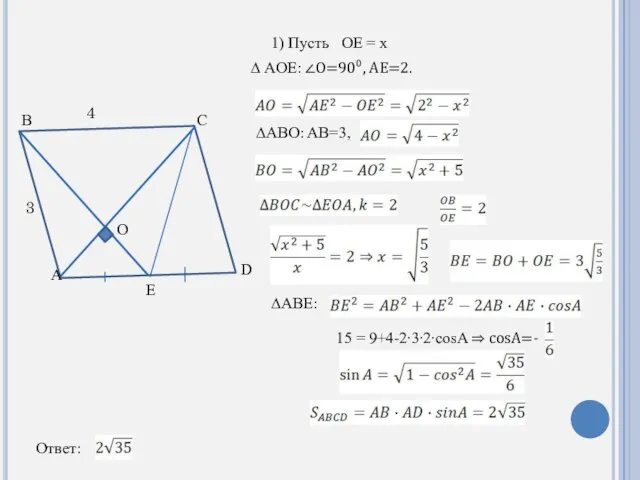
- 11. O A B C D E 1) Пусть OE = x 3 4 ∆ AOE: ∠O=90⁰,
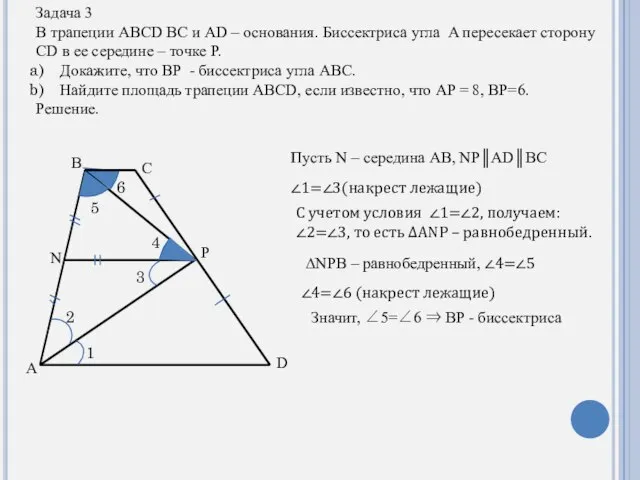
- 12. Задача 3 В трапеции ABCD BC и AD – основания. Биссектриса угла A пересекает сторону CD
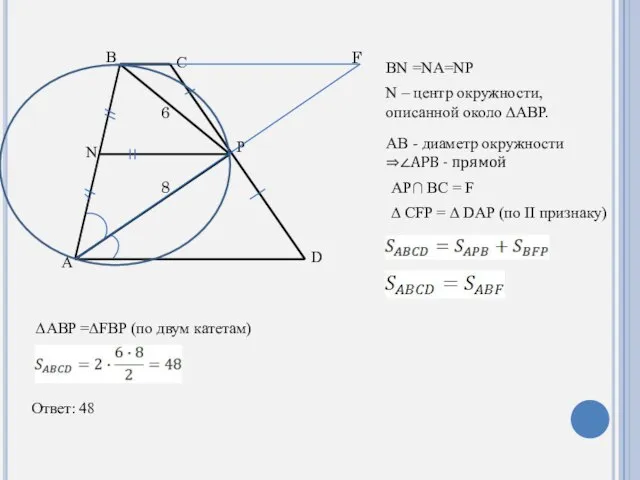
- 13. D C B A P N BN =NA=NP N – центр окружности, описанной около ∆ABP. AB
- 14. Задача №4 В равнобедренной трапеции ABCD точки M и N- середины оснований BC и AD соответственно.
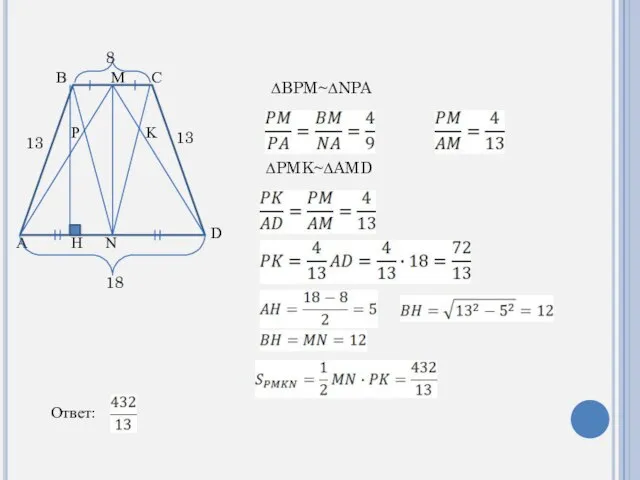
- 15. A B C D M N P K 13 13 18 8 H ∆BPM~∆NPA ∆PMK~∆AMD Ответ:
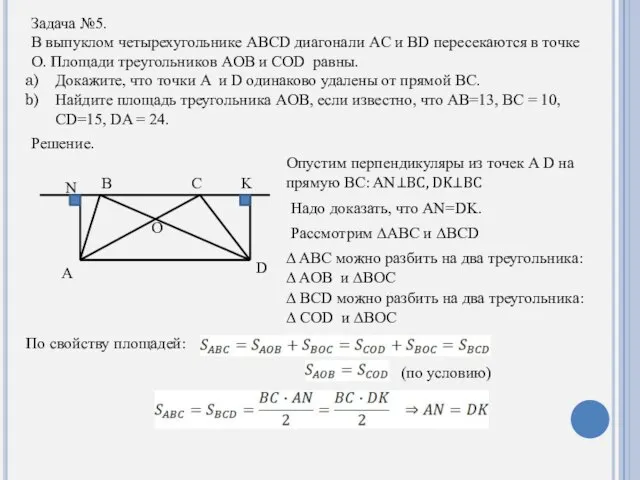
- 16. Задача №5. В выпуклом четырехугольнике ABCD диагонали AC и BD пересекаются в точке O. Площади треугольников
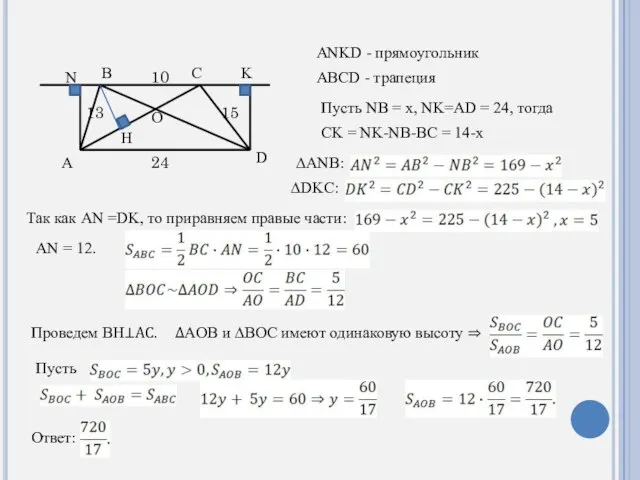
- 17. A N D K C B O 13 15 10 24 H ANKD - прямоугольник ABCD
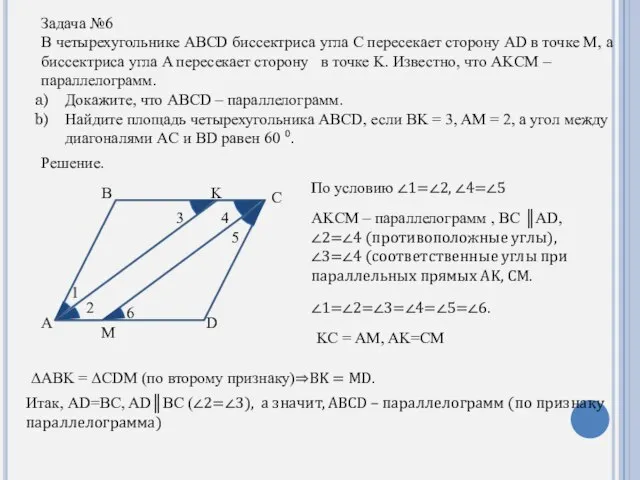
- 18. Задача №6 В четырехугольнике ABCD биссектриса угла C пересекает сторону AD в точке M, а биссектриса
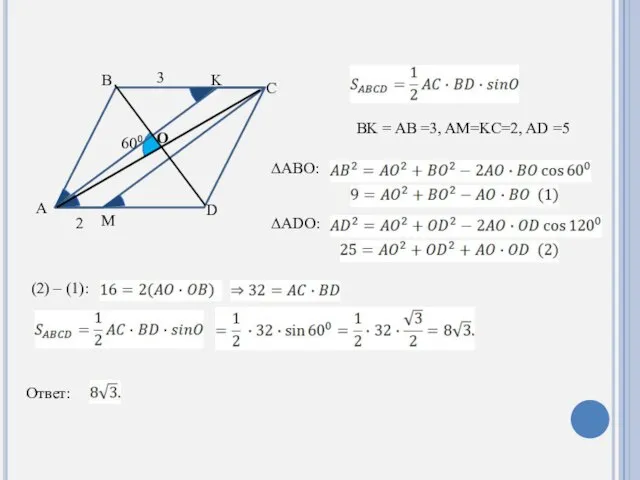
- 19. A D M K B C O 60⁰ 3 2 BK = AB =3, AM=KC=2, AD
- 21. Скачать презентацию






 Центральная симметрия
Центральная симметрия Логарифмические уравнения
Логарифмические уравнения Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Признак существования определенного интеграла. Лекция №7
Признак существования определенного интеграла. Лекция №7 Дифференциальные уравнения I порядка с разделяющимися переменными
Дифференциальные уравнения I порядка с разделяющимися переменными Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем
Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы
Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел Логика. Введение
Логика. Введение Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Занимательная математика. 2 класс
Занимательная математика. 2 класс Презентация на тему РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ
Презентация на тему РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ  Комплексные числа и действия над ними
Комплексные числа и действия над ними Умножение натуральных чисел 5 класс
Умножение натуральных чисел 5 класс Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс) 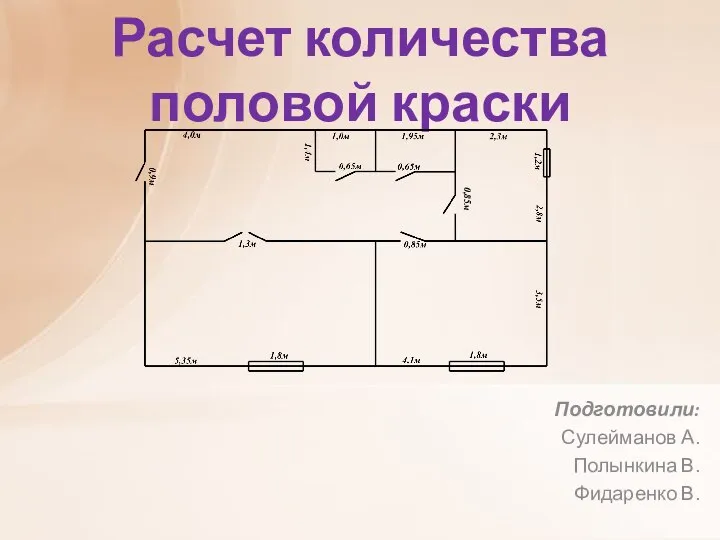 Расчет количества половой краски
Расчет количества половой краски Классическое определение вероятности
Классическое определение вероятности Длина окружности. Площадь круга
Длина окружности. Площадь круга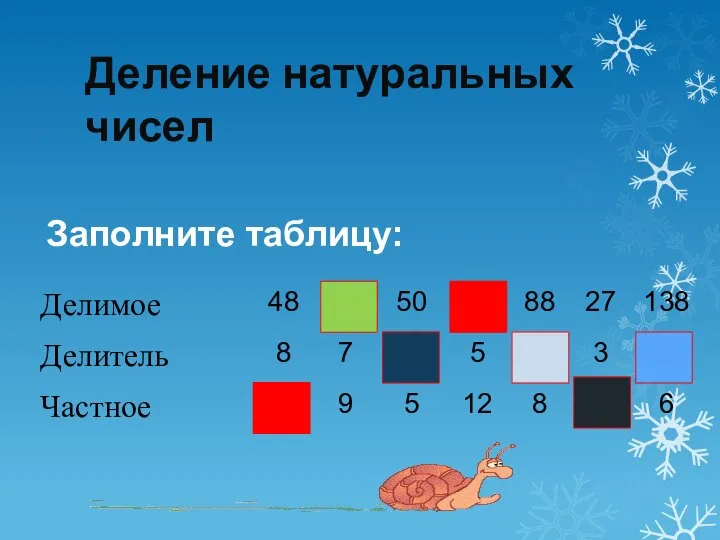 Деление натуральных чисел
Деление натуральных чисел Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики
Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики Презентация на тему Разность квадратов
Презентация на тему Разность квадратов  Дроби вокруг нас
Дроби вокруг нас Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Алгебра логики
Алгебра логики Линейные операции над векторами
Линейные операции над векторами Анализ контрольной работы
Анализ контрольной работы