Множества и отношения

Множества
Основные определения
Алгебра множеств
Представление множеств
Вопросы

Множества. Основные определения
Множество - это совокупность определенных различимых объектов, для каждого из которых можно установить, принадлежит этот объект данному множеству или нет. Различимые объекты называются элементами множества.
Обозначения «наивной» теории множеств
а ∈ А - элемент а принадлежит множеству A
а ∉ A - элемент a не принадлежит A

Множества. Основные определения
Способы задания множеств
прямым перечислением всех элементов A = {a, b, c, … , z }
множество простых чисел, не превосходящих 10: { 2, 3, 5, 7} ;
множество всех месяцев года : { январь, февраль, … , декабрь };
множество всех натуральных чисел: ℕ = {1,2,3, …}.
характеристическим предикатом A = {a | P(a) }
множество целых степеней двойки: S2 = {s | s = 2k, k ∈ ℕ };
множество четных чисел: { x | x – четно, x ∈ℤ }.
порождающей процедурой A = {a | a:=f }
множество однозначных чисел: N1 = { n | for n:= 1 to 9 do write(n); };
множество чисел Фибоначчи: F = { fi | f1 = f2 = 1; fn+2 = fn + fn+1 , i ∈ℕ }.

Множества. Основные определения
Универсальное множество или универсум есть множество U, состоящее из элементов всех рассматриваемых множеств.
Пример: Пусть A = { 1, 3, 5 }, D = { 2, 3, 8 }, N = { 4 }.
Тогда U = { 1, 2, 3, 4, 5, 8 }.
Пустое множество – это множество без элементов.
∅ = { }
Семейство - множество, элементами которого являются множества.
Пример: Пусть A = { 1, 3, 5 }, D = { 2, 3, 8 }.
Тогда N = { A, D, 5 } = { { 1 ,3 ,5 }, { 2 ,3 ,8 }, 5 }.

Множества. Основные определения
Мультимножество – совокупность элементов, в которые элементы входят по нескольку раз.
расписание занятий – один и тот же предмет повторяется несколько раз;
штатное расписание – одна и та же должность повторяется несколько раз.
Обозначения:
X = 〈 a, … , a; b, … , b; … ; z, … , z 〉 = [an1, bn2, … , znk] – мультимножество
n1 n2 nk
A = {a, b, c, … , z} – носитель мультимножества
n1, n2 ,…, nk – показатели элементов мультимножества
Пример:
Пусть A = {a, b, c}. Тогда X = [a0,b3,c4] = 〈 b, b, b; c, c, c, c 〉

Множества. Алгебра множеств
Сравнение множеств
Множество A является подмножеством множества B, если любой элемент множества A принадлежит множеству B
A ⊂ B ⟺ ( x ∈ A ) ⇒ ( x ∈ B ).
Говорят: множество A содержится в множестве B
(множество B включает множество A).
Два множества равны, если они являются подмножествами друг друга
A = B ⟺ A ⊂ B и B ⊂ A
Свойства: 1. ∀A ( A ⊂ A );
2. ∀A, B (( A ⊂ B и B ⊂ A ) ⇒ ( A = B ));
3. ∀A, B, C (( A ⊂ B и B ⊂ С ) ⇒ ( A ⊂ С )).

Множества. Алгебра множеств
Мощность множеств. Сравнение мощностей
Множество A называется собственным подмножеством множества B, если A ⊂ B и A ≠ B .
Равномощными называются множества, между элементами которых можно установить взаимно-однозначное
соответствие, т.е. |A| = |B| ⟺ A ~ B.
Пример: Пусть ℕ - множество натуральных чисел,
N2 - множество четных натуральных чисел. Очевидно, N2 ⊂ ℕ и N2 ≠ ℕ .
ℕ: 1 2 3 … n …
⇒ ℕ ~ N2 или |ℕ | = | N2 |.
N2 : 2 4 6 … 2n …
Свойства: 1. ∀A (|A| = |A| );
2. ∀A, B (|A| = |B| ⇒ |B| = |A| );
3. ∀A, B, C ((|A| = |B| и |B| = |C|) ⇒ (|A| = |C|)).

Множества. Алгебра множеств
Мощность множеств. Сравнение мощностей
Конечным называется такое множество A, у которого не существует равномощного собственного
подмножества, т.е.
∀B (( B ⊂ A и |B| = |A|) ⇒ ( B = A ))
Обозначение: |A| < ∞
Бесконечным называется такое множество, которое равномощно некоторому своему собственному
подмножеству, т.е.
∃B ( B ⊂ A и |B| = |A| и B ≠ A )
Обозначение: |A| = ∞

Множества. Алгебра множеств
Операции над множествами
Объединение A ∪ B = { x | x ∈ A или x ∈ B }
Пересечение A ∩ B = { x | x ∈ A и x ∈ B }
Разность A \ B = { x | x ∈ A и x ∉ B }
Симметрическая разность
A ∆ B = (A ∪ B) \ (A ∩ B) = (A \ B) ∪ (B \ A)
Дополнение A = { x | x ∉ A } = U \ A, где U – универсум.

Множества. Алгебра множеств
Объединение
A ∪ B = { x | x ∈ A или x ∈ B }
Свойства
Идемпотентность А ∪ А = A
Коммутативность А ∪ В = В ∪ А
Ассоциативность А ∪ (В ∪ С) = (А ∪ В) ∪ С = А ∪ В ∪ С
свойство нуля А ∪ ∅ = А
свойство единицы А ∪ U = U

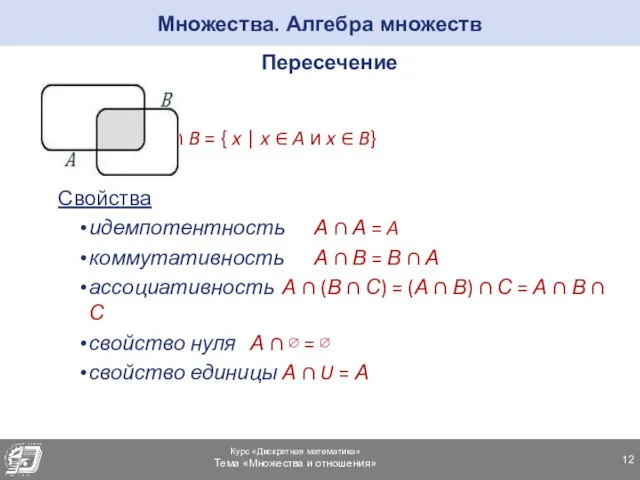
Множества. Алгебра множеств
Пересечение
A ∩ B = { x | x ∈ A и x ∈ B}
Свойства
идемпотентность А ∩ А = A
коммутативность А ∩ В = В ∩ А
ассоциативность А ∩ (В ∩ С) = (А ∩ В) ∩ С = А ∩ В ∩ С
свойство нуля А ∩ ∅ = ∅
свойство единицы А ∩ U = А

Множества. Алгебра множеств
Разность
B \ A = { x | x ∈ B и x ∉ A}
Свойства
свойства нуля А \ ∅ = А ∅ \ А = ∅
свойства единицы А \ U = ∅ U \ А = A

Множества. Алгебра множеств
Симметрическая разность
A ∆ B = (A ∪ B) \ (A ∩ B) = (A \ B) ∪ (B \ A)
Свойства
коммутативность А ∆ В = В ∆ А
Ассоциативность А ∆ (В ∆ С) = (А ∆ В) ∆ С = А ∆ В ∆ С
свойство нуля А ∆ ∅ = А
свойство единицы А ∆ U = А

Множества. Алгебра множеств
Разбиения. Покрытия
Семейство множеств F = { Fi } называется покрытием множества B, если для любого элемента множества B найдется подмножество Fi, которому он принадлежит, т.е.
∀ x ∈ B ( ∃Fi ( x ∈ Fi ))
Покрытие называется разбиением множества B, если :
1. ∀i ( Fi ⊂ B )
2. ∀ i,j ( i ≠ j ⇒ Fi ∩ Fj = ∅ ) , т.е. никакие два подмножества покрытия не пересекаются
Пример: Пусть A = {1, 2, 3 }. Тогда
{{1, 2}, {2, 3}, {3, 1}} – покрытие множества A, но не разбиение;
{{1}, {2}, {3}} – разбиение множества A;
{{∅}, {1}, {3}} - не является ни покрытием, ни разбиением.

Множества. Алгебра множеств
Булеан
Булеаном множества А называется множество всех подмножеств множества А и обозначается как 2A или P(А).
Обозначение: 2A = P(A) = { B | B ⊂ A }
Теорема: Если множество A - конечно, то |2A| = 2|A|.
Пример:
Если A = { 1, 2, 3 }, то
2A = { ∅, {1}, {2}, {3}, {1,2}, {1, 3}, {2, 3}, {1, 2, 3} }.
Если A = ∅, то
|2A| = 2|A| = 21 = 2, т.е. 2A = {∅, {∅}}.

Множества. Алгебра множеств
Алгебра множеств – множество всех подмножеств множества U с операциями пересечения, объединения, разности и дополнения.
Обозначение: 2U =
U – носитель алгебры
{ ∩, ∪, \, ¬ } – сигнатура алгебры

Множества. Алгебра множеств
Законы алгебры множеств
Дистрибутивный A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Закон поглощения (A ∩ B) ∪ A = A
(A ∪ B) ∩ A = A
Законы де Моргана (A ∪ B) = A ∩ B
(A ∩ B) = A ∪ B
Выражение для разности A \ B = A ∩ B
Закон двойного отрицания A = A

Массив
Связанный список
Двоичный вектор
Представление множеств

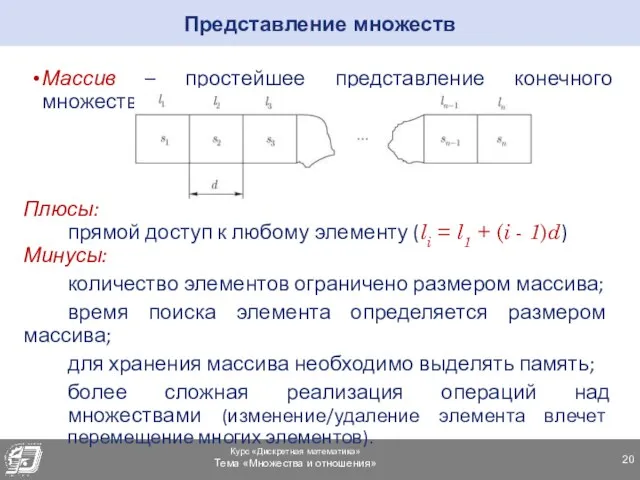
Массив – простейшее представление конечного множества,
Плюсы:
прямой доступ к любому элементу (li = l1 + (i - 1)d)
Минусы:
количество элементов ограничено размером массива;
время поиска элемента определяется размером массива;
для хранения массива необходимо выделять память;
более сложная реализация операций над множествами (изменение/удаление элемента влечет перемещение многих элементов).
Представление множеств

Характеристический вектор – разновидность последовательного распределения
Длина вектора – мощность универсума |U|
Пример: U = {1, 2, 3, 4, 5, 6 , 7, 8, 10}
P = {2, 3, 5, 7} – множество простых чисел
vp = (0 1 1 0 1 0 1 0 0) – вектор множества P
Плюсы:
легко изменять список (место каждого элемента известно)
Минусы:
ограниченность количества элементов множества;
необходимость упорядочивания элементов множества;
неэкономичность в случае «редкого» распределения.
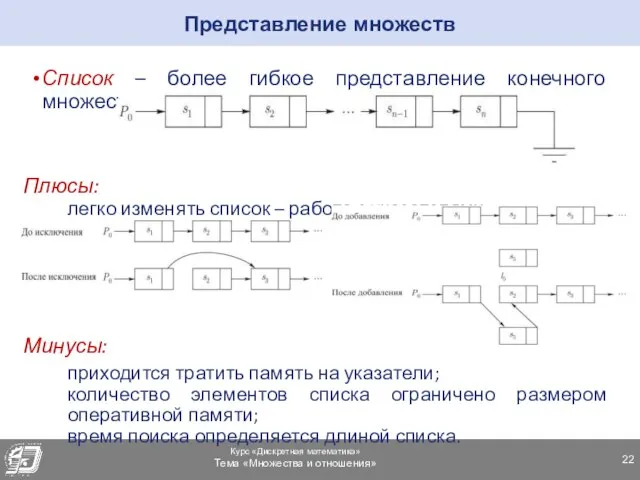
Представление множеств

Список – более гибкое представление конечного множества,
Плюсы:
легко изменять список – работа с указателями
Пример:
Минусы:
приходится тратить память на указатели;
количество элементов списка ограничено размером оперативной памяти;
время поиска определяется длиной списка.
Представление множеств

Словари (справочники)
Хэш – таблицы (системы представителей)
Очереди с приоритетами (задачи планирования)
Базы данных (знаний)
Применение множеств