Слайд 2Функцию f(x), xϵX называют четной, если для любого значения х из множества

Х выполняется равенство:
f(-x)=f(x)
Функцию f(x), xϵX называют нечетной, если для любого значения х из множества Х выполняется равенство:
f(-x)=-f(x)
Слайд 3Если числовое множество Х вместе с каждым своим элементом х содержит и

противоположный элемент -х, то такое множество называют симметричным множеством.
Например: отрезок [-5, 5] ̶ симметричное множество, а отрезок [-4, 5] ̶ не симметричное множество (в него входит число 5, но не входит противоположное ему -5)
Слайд 4График четной функции симметричен относительно оси у.
Если график функции y=f(x), хϵХ симметричен
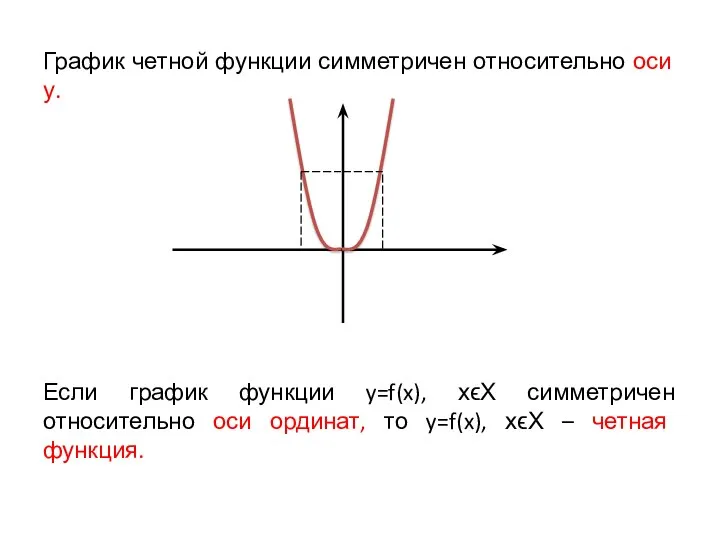
относительно оси ординат, то y=f(x), хϵХ – четная функция.
Слайд 5График нечетной функции симметричен относительно начала координат.
Если график функции y=f(x), хϵХ симметричен
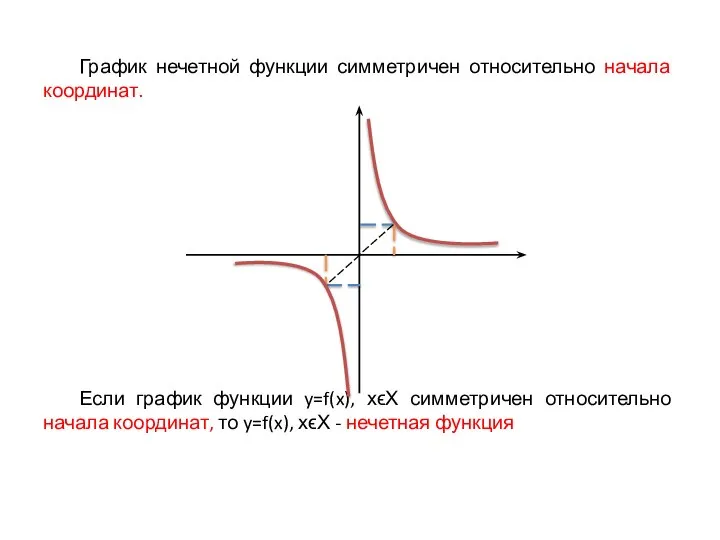
относительно начала координат, то y=f(x), хϵХ - нечетная функция
Слайд 6Если функция у=f(x), хϵХ четная или нечетная, то ее область определения Х

– симметричное множество.
Если же Х – несимметричное множество, то функция у=f(x), хϵХ не может быть ни четной ни нечетной.
Слайд 7Алгоритм исследования функции y=f(x), хϵХ на четность.
Установить, симметрична ли область определения

функции.
Если нет, функция не является ни четной, ни нечетной. Если да, то перейти ко второму шагу алгоритма.
2) Составить выражение f(-x).
Сравнить f(-x) и f(x):
а) если f(-x)=f(x), то функция четная;
б) если f(-x)=-f(x), то функция нечетная;
в) если хотя бы в одной точке хϵХ выполняется соотношение f(-x)≠f(x) и хотя бы в одной точке хϵХ выполняется соотношениеf(-x)≠-f(x), то функция не является ни четной, ни нечетной.
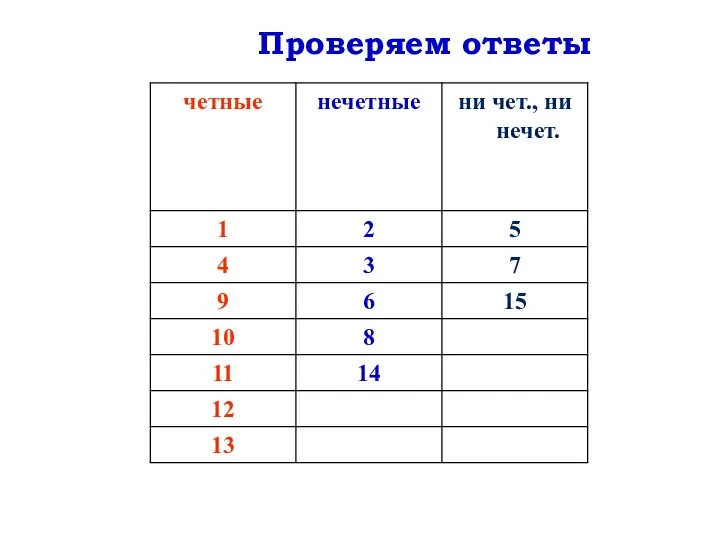
Слайд 16 Разбейте функции на три группы:
четные
нечетные
не являются ни

четными, ни нечетными














 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Презентация на тему ГИА 2013 Модуль «Геометрия» № 11
Презентация на тему ГИА 2013 Модуль «Геометрия» № 11  Азбука
Азбука Операции и алгебры
Операции и алгебры Формула полной вероятности и формула Байеса
Формула полной вероятности и формула Байеса Векторы в пространстве
Векторы в пространстве Теория вероятностей и математическая статистика. Многомерные распределения вероятностей
Теория вероятностей и математическая статистика. Многомерные распределения вероятностей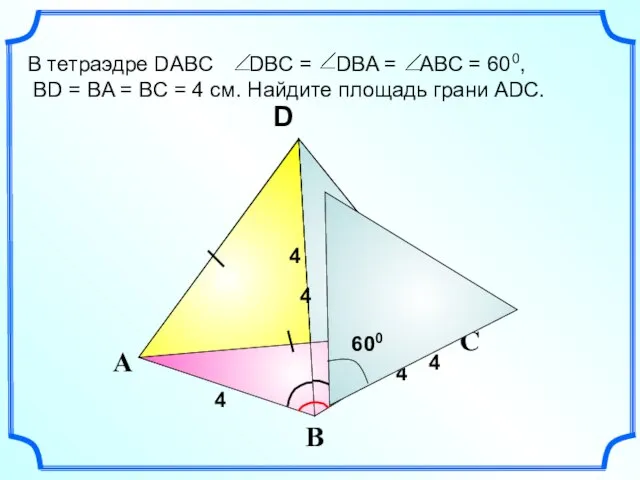 Тетраэдр. Свойства тетраэдра
Тетраэдр. Свойства тетраэдра Тест Проверь себя! Чему ты научился в первом классе?
Тест Проверь себя! Чему ты научился в первом классе? Презентация на тему Измерение углов
Презентация на тему Измерение углов  Числовой коэффициент
Числовой коэффициент Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Прямоугольный треугольник. Задачи. 7 класс
Прямоугольный треугольник. Задачи. 7 класс Преобразование сумм тригонометрических функций в произведения. Преобразование простейших тригонометрических выражений
Преобразование сумм тригонометрических функций в произведения. Преобразование простейших тригонометрических выражений Вычитание чисел. Решение уравнений
Вычитание чисел. Решение уравнений Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Множества и его элементы
Множества и его элементы Организация экспериментов с использованием системных принципов
Организация экспериментов с использованием системных принципов Скалярное произведение в евклидовом и унитарном пространстве
Скалярное произведение в евклидовом и унитарном пространстве Тренировочная работа по математике
Тренировочная работа по математике Презентация на тему Сложение целых чисел
Презентация на тему Сложение целых чисел  Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Стереометрия. Школьный курс
Стереометрия. Школьный курс Предел функции в точке
Предел функции в точке Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Тайны математики 2
Тайны математики 2 Cтереометрия
Cтереометрия Выборочное наблюдение
Выборочное наблюдение