- Главная
- Математика
- Моменты случайной величины

Содержание
Слайд 2
коэффициент асимметрии
Если А>0, то кривая распределения более полога справа от моды.
коэффициент асимметрии
Если А>0, то кривая распределения более полога справа от моды.

Если А<0, то кривая распределения более полога слева от моды.
Для нормального закона распределения А=0.
μ4 – характеристика крутости (островершинности или плосковершинности) распределения.
- коэф-т эксцесса.
Для нормального распределения Е=0.
Если некоторое распределение имеет Е≠0, то кривая этого распределения отличается от нормальной кривой.
Если E>0, то кривая имеет более высокую и острую вершину, чем нормальная кривая.
Если E<0, то сравниваемая кривая имеет более низкую и плоскую вершину, чем норм. кривая.
При этом, нормальное и сравниваемое с ним распределение имеют одинаковые м.о. и дисперсии.
Для нормального закона распределения А=0.
μ4 – характеристика крутости (островершинности или плосковершинности) распределения.
- коэф-т эксцесса.
Для нормального распределения Е=0.
Если некоторое распределение имеет Е≠0, то кривая этого распределения отличается от нормальной кривой.
Если E>0, то кривая имеет более высокую и острую вершину, чем нормальная кривая.
Если E<0, то сравниваемая кривая имеет более низкую и плоскую вершину, чем норм. кривая.
При этом, нормальное и сравниваемое с ним распределение имеют одинаковые м.о. и дисперсии.
Слайд 4Распределение функций нормальных с.в.
Распределение функций нормальных с.в.

Слайд 5.
.
.
.
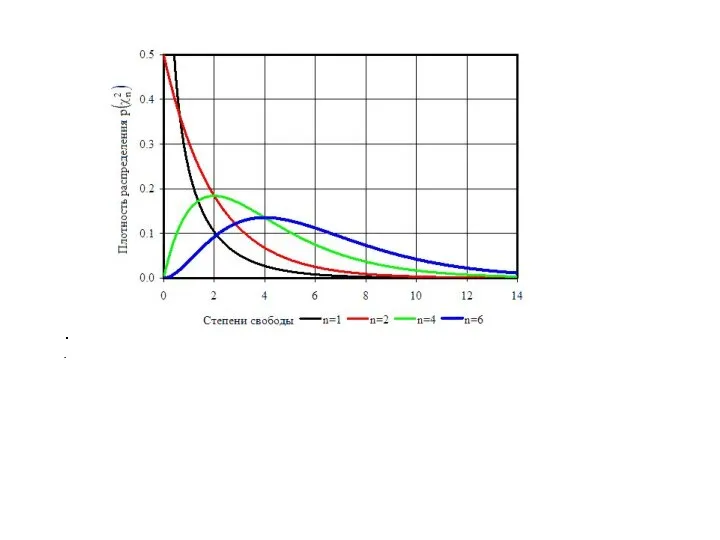
Слайд 6Распределение Стьюдента
(t- распределение).
Пусть
имеет распределение Стьюдента с к степенями свободы
Распределение Стьюдента
(t- распределение).
Пусть
имеет распределение Стьюдента с к степенями свободы

Следующая -
Концепция публичных арен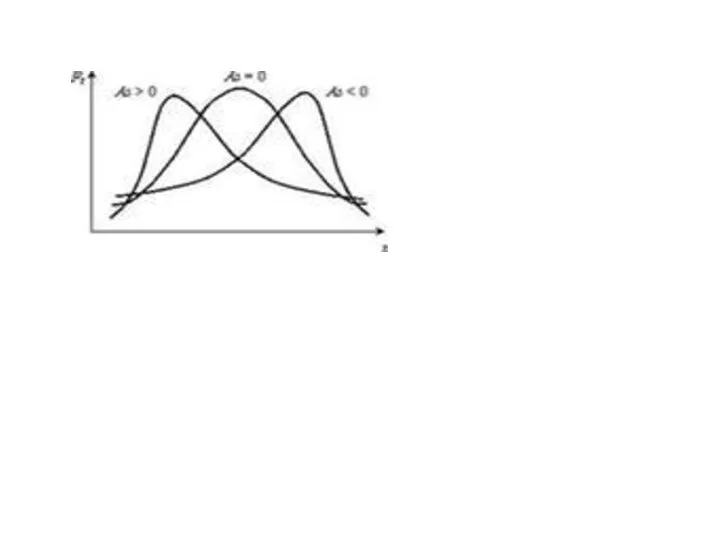
 Деление. Задания
Деление. Задания Исследование функции на монотонность. Экстремумы функции. Построение графиков функций с применением производной
Исследование функции на монотонность. Экстремумы функции. Построение графиков функций с применением производной Системы тригонометрических уравнений
Системы тригонометрических уравнений Сложение чисел
Сложение чисел Решение задач по теме Многогранники
Решение задач по теме Многогранники Занимательная математика (3 класс)
Занимательная математика (3 класс) Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Подготовка к ВПР
Подготовка к ВПР Линейное уравнение с двумя переменными и его график. 7 класс
Линейное уравнение с двумя переменными и его график. 7 класс Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Площадь четырехугольника
Площадь четырехугольника Среднее арифметическое в поисках сокровищ
Среднее арифметическое в поисках сокровищ Практическое применение подобия треугольников
Практическое применение подобия треугольников Признаки параллельности прямых
Признаки параллельности прямых Правило нахождения первообразной
Правило нахождения первообразной Решение уравнений с модулем
Решение уравнений с модулем Правильная треугольная усечённая пирамида
Правильная треугольная усечённая пирамида Презентация по математике "Основы концепции “глубинного анализа текстов" -
Презентация по математике "Основы концепции “глубинного анализа текстов" -  Вычитание смешанных чисел
Вычитание смешанных чисел Презентация на тему Обьёмные тела и многогранники
Презентация на тему Обьёмные тела и многогранники  Площадь. Площадь трапеции
Площадь. Площадь трапеции Решение логарифмических уравнений
Решение логарифмических уравнений Динамика системы вблизи цикла
Динамика системы вблизи цикла Многочлены над числовыми полями
Многочлены над числовыми полями Способ группировки
Способ группировки Задачи с параметром в материалах Государственной итоговой аттестации и методы их решения (По материалам ЕГЭ за последние 5лет)
Задачи с параметром в материалах Государственной итоговой аттестации и методы их решения (По материалам ЕГЭ за последние 5лет) Веселые примеры
Веселые примеры Предел функции (часть 2)
Предел функции (часть 2)