Содержание
- 2. Линейная зависимость от нескольких объясняющих переменных 2 Парные коэффициенты корреляции ryx(i) не учитывают влияние на эту
- 3. Частные (очищенные) коэффициенты корреляции 3 – частный коэффициент корреляции, коэффициент кор-реляции между переменными x(i) и x(j)
- 4. Численные примеры 4 n = 37 – число исследуемых предприятий легкой промышленности, x(0) ≡ y –
- 5. Численные примеры 5 n = 20 – число лет метеонаблюдений, x(0) ≡ y – урожайность кормовых
- 6. Множественный коэффициент корреляции 6 Множественный коэффициент корреляции – коэффициент корреляции между y и линейной функцией регрессии,
- 7. Множественный коэффициент корреляции 7 Свойства множественного коэффициента корреляции: 3. Вычисление МКК по частным коэффициентам корреляции: 4.
- 8. Проверка гипотезы о наличии множественной линейной связи 8 1. Выбираем уровень значимости α. Типичные значения α
- 9. Корреляционный анализ порядковых переменных 9 Типовые задачи: 1. Анализ структуры упорядочений. Точки разбросаны равномерно, нет согласованности
- 10. Ранговый коэффициент корреляции Спирмена 10 Базовая формула: Свойства коэффициента Спирмена: m(k) – число групп объединенных рангов,
- 11. Численные примеры 11 10 инвестиционных проектов, проранжированных 2 экспертами. Пример 1: 10 стран, проранжированных по уровню
- 12. Ранговый коэффициент корреляции Кендалла 12 Базовая формула: Свойства коэффициента Кендалла: минимальное число обменов со-седних элементов переменной
- 13. Ранговый коэффициент корреляции Кендалла 13 Формула для случая объединенных рангов: Пример 1: Пример 2:
- 14. Проверка гипотезы о наличии связи между порядковыми переменными 14 Связь есть, если или 0,915 > СТЬЮДРАСПОБР
- 15. Связь между несколькими порядковыми переменными 15 Коэффициент конкордации: n – число объектов, m – число переменных,
- 16. Численный пример 16 Ранжировка 10 инвестиционных проектов, осуществленная 3 экспертами. 2 2 2 2 2 4
- 17. Проверка гипотезы о наличии связи между несколькими порядковыми переменными 17 Связь есть, если Пример 1: 22,35
- 18. Корреляционный анализ категоризованных переменных 18 x(1), x(2) – категоризованные переменные (переменные, описываемые конечным числом состояний). ##
- 19. Случаи тесной связи и независимости переменных 19 ## x(1) – пол (муж/жен), x(2) – уровень зарплаты
- 20. Квадратичная сопряженность –характеристика тесноты связи 20 Квадратичная сопряженность: два способа расчета: Проверка гипотезы о наличии связи:
- 21. Численный пример 21 Зависимость оплаты труда (низкая; средняя; высокая) от образования (неполное среднее; среднее; среднее специальное;
- 23. Скачать презентацию




















 Площадь. Фигуры
Площадь. Фигуры Векторное кодирование графической информации. Практическая работа. 6 класс
Векторное кодирование графической информации. Практическая работа. 6 класс Простейшие задачи в координатах
Простейшие задачи в координатах Контрольная работа №8 по теме Разложение многочленов на множители
Контрольная работа №8 по теме Разложение многочленов на множители Использование занимательных игровых упражнений при обучении элементарной математики для развития логического мышления дошкольн
Использование занимательных игровых упражнений при обучении элементарной математики для развития логического мышления дошкольн Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Презентация на тему Решение неравенств методом интервалов
Презентация на тему Решение неравенств методом интервалов  Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Математические ребусы. 4 класс
Математические ребусы. 4 класс Презентация на тему Объём шара и его частей
Презентация на тему Объём шара и его частей  Метод деформируемого многогранника (Нелдера-Мида)
Метод деформируемого многогранника (Нелдера-Мида) Таблица умножения на 2
Таблица умножения на 2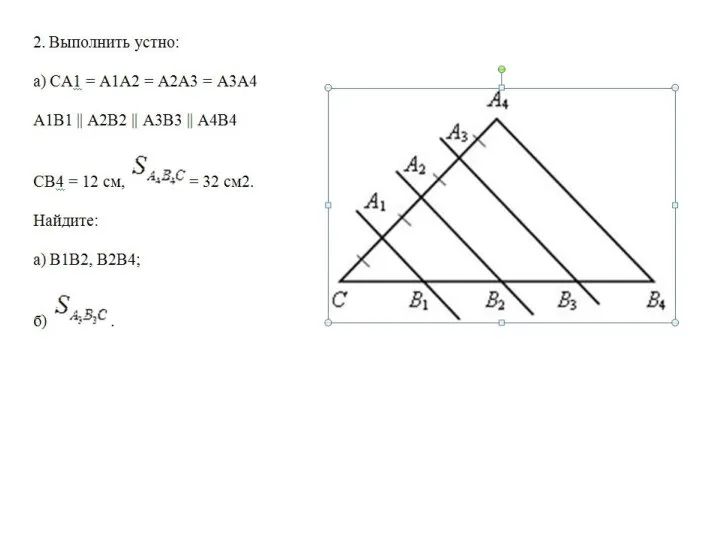 Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3) Комплексные числа
Комплексные числа По какому принципу образован ряд
По какому принципу образован ряд Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Решение треугольников
Решение треугольников Углы. Математический диктант
Углы. Математический диктант Теория вероятностей
Теория вероятностей Задача № 106
Задача № 106 Презентация на тему Занимательная математика
Презентация на тему Занимательная математика  Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Площа фігури. Задачі на спільну роботу
Площа фігури. Задачі на спільну роботу Методы кластеризации
Методы кластеризации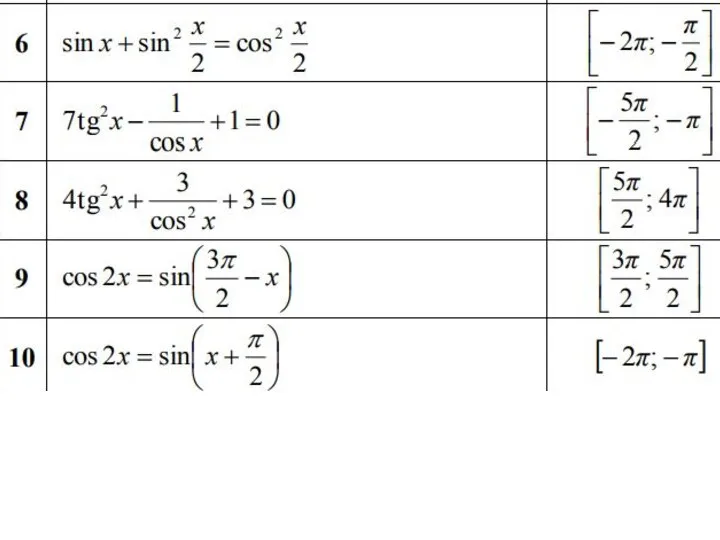 Решение уравнений
Решение уравнений Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Математическая статистика. Лекция 2
Математическая статистика. Лекция 2