Содержание
- 2. Тема урока Объём конуса
- 3. Сократ (470 – 380 гг. до н. э.) « Пусть сюда не входит никто, не знающий
- 4. Основные задачи урока Обобщить сведения о конусе. Формула для вычисления объёма конуса. Научиться решать задачи на
- 5. План урока Повторение основных сведений о конусе. Историческая справка. Новый материал. Решение задач. Дополнительная информация о
- 6. Решите задачу Основание пирамиды – прямоугольник со сторонами 6 и 8см. Найдите объем пирамиды, если все
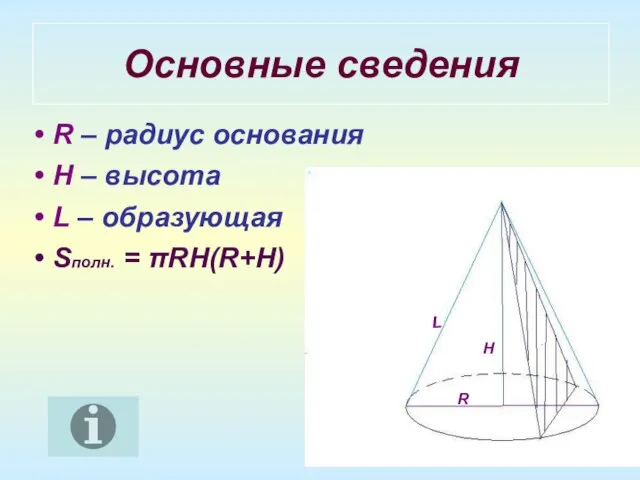
- 7. Основные сведения R – радиус основания H – высота L – образующая Sполн. = πRH(R+H) L
- 8. Тема урока конуса объём
- 9. Историческая справка Конус в переводе с греческого «konos» означает «сосновая шишка». Демокрит (470-380 гг. до н.э.)
- 10. Теорема Объем конуса равен одной трети произведения площади основания на высоту
- 11. Новый материал
- 12. Объем конуса.
- 13. Следствие Объем усеченного конуса, высота которого равна h, а площади основания равны S и S вычисляется
- 14. Смолу для промышленных нужд собирают, подвешивая конические воронки к соснам. Сколько воронок диаметром 10 см с
- 15. Задача №2 Авиационная бомба среднего калибра даёт при взрыве воронку диаметром 6м и глубиной 2 м.
- 16. Дополнительная информация В геологии – «конус выноса». В биологии – «конус нарастания». «Конусами» называется семейство морских
- 17. Практическое применение конические детали в машинах и механизмах; в автомобилях, танках, бронетранспортёрах – конические шестерни; носовая
- 18. Практическое применение
- 19. Практическое применение
- 20. Практическое применение
- 21. « Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и
- 23. Скачать презентацию



















 Умножение и деление десятичной дроби на единицу с нулями
Умножение и деление десятичной дроби на единицу с нулями Угол между двумя плоскостями
Угол между двумя плоскостями Дискретная математика
Дискретная математика Примеры +7, +8, +9
Примеры +7, +8, +9 Смежные и вертикальные углы
Смежные и вертикальные углы Дифференцирование сложной функции
Дифференцирование сложной функции Первый признак равенства треугольников
Первый признак равенства треугольников Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс
Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс  Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Сложение вида +5. Путешествие в космос
Сложение вида +5. Путешествие в космос Сложение и вычитание целых и дробных чисел
Сложение и вычитание целых и дробных чисел Задачи на проценты
Задачи на проценты Определение производной. Правила вычисления производных. Таблица производных
Определение производной. Правила вычисления производных. Таблица производных 6. СЛАУ. Методы решения (1)
6. СЛАУ. Методы решения (1) Квадратичная функция. Её свойства и график
Квадратичная функция. Её свойства и график Числовые ряды. Признаки сходимости
Числовые ряды. Признаки сходимости Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс 2.МатСтатистика-Критерии и Различия
2.МатСтатистика-Критерии и Различия Область определения функции
Область определения функции Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Графики функций
Графики функций Стереометрия, планиметрия. Основные понятия. (Геометрия. Задания 14, 16)
Стереометрия, планиметрия. Основные понятия. (Геометрия. Задания 14, 16) Равенство треугольников и их элементов. Решение задач
Равенство треугольников и их элементов. Решение задач Презентация на тему Единицы измерения
Презентация на тему Единицы измерения  Проект по математике. Цифра 5. 1 класс
Проект по математике. Цифра 5. 1 класс Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы  Степенная функция
Степенная функция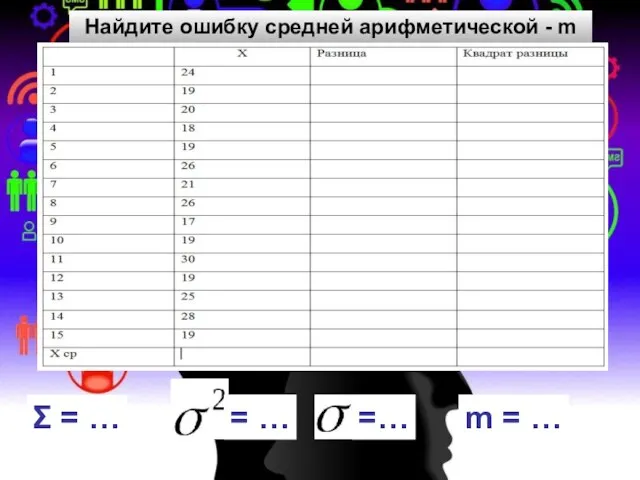 Средняя арифметическая
Средняя арифметическая