Содержание
- 2. План лекции Множества: понятия и операции над множествами Основные принципы комбинаторики (правила сложения и умножения) принцип
- 3. Лаплас: "...теория вероятностей есть в сущности не что иное, как здравый смысл, сведенный к исчислению."
- 4. Элементы теории множеств Множество – это совокупность некоторых предметов (объектов), объединенных в одно целое по какому-либо
- 5. Способы задания множеств Перечисление его элементов A = {1; 2; 3; 4; 5; 6; 7; 8;
- 6. Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то
- 7. Подмножества Если каждый элемент множества А является также элементом множества В, то А – подмножество множества
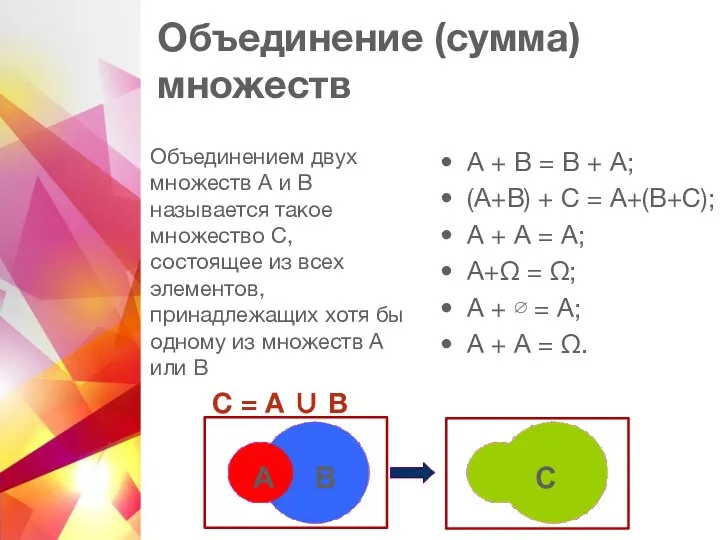
- 8. Объединение (сумма) множеств Объединением двух множеств А и В называется такое множество С, состоящее из всех
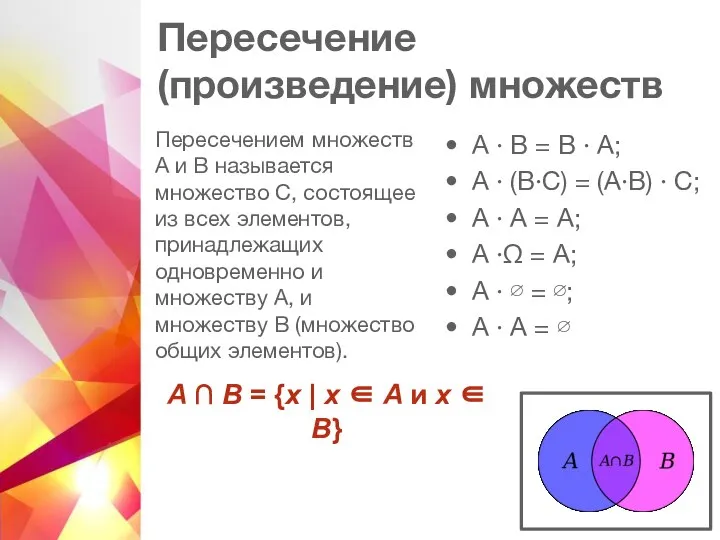
- 9. Пересечение (произведение) множеств Пересечением множеств А и В называется множество С, состоящее из всех элементов, принадлежащих
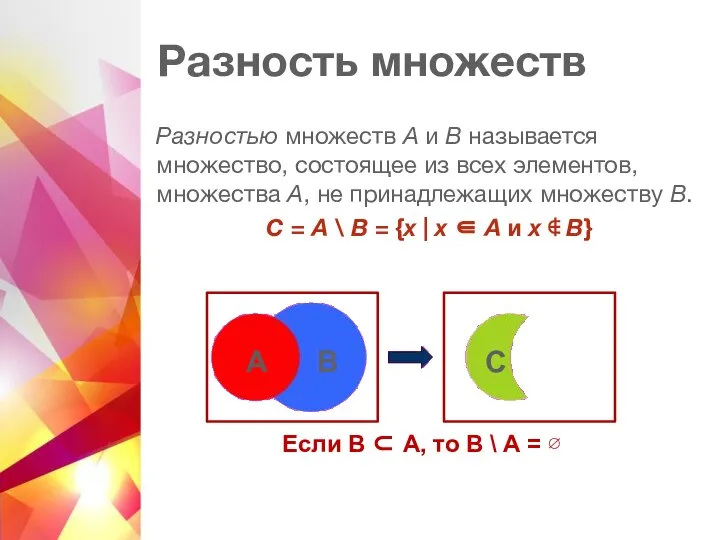
- 10. Разность множеств Разностью множеств А и В называется множество, состоящее из всех элементов, множества А, не
- 11. ОСНОВНЫЕ ПРИНЦИПЫ КОМБИНАТОРИКИ
- 12. Определение Комбинаторика или теория конечных множеств – это раздел математики, в котором изучаются вопросы о том,
- 13. 1. Правило сложения Пусть есть два множества объектов: А = {a1, a2, … an} и B
- 14. 1. Правило сложения. Пример 1 А = {а, б, ..., ё, …, я} |A| = 33
- 15. 2. Правило умножения Пусть А = {a1, a2, … an}, B = {b1, b2, … bm}
- 16. 2. Правило умножения Пример 2 А = {а, б, ..., ё, …, я} |A| = 33
- 17. Следствие из правила умножения Пусть у нас есть множества А1, ... Аk, каждое из которых состоит
- 18. 3. Принцип Дирихле Есть n ящиков и n+1 кролик. Как ни рассаживай кроликов по ящикам найдется
- 20. Скачать презентацию














 Характер и ритм линий как средство выражения
Характер и ритм линий как средство выражения Задачи по геометрии
Задачи по геометрии Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе
Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве Урок-игра. Пик знаний.Тригонометрически функции
Урок-игра. Пик знаний.Тригонометрически функции Окружность. Вписанные углы
Окружность. Вписанные углы Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Метрическая система мер
Метрическая система мер Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) Преобразование тригонометрических графиков
Преобразование тригонометрических графиков Математика и мир искусства
Математика и мир искусства Дискретная математика. Задание №2. Матрица инцидентности неориентированного графа
Дискретная математика. Задание №2. Матрица инцидентности неориентированного графа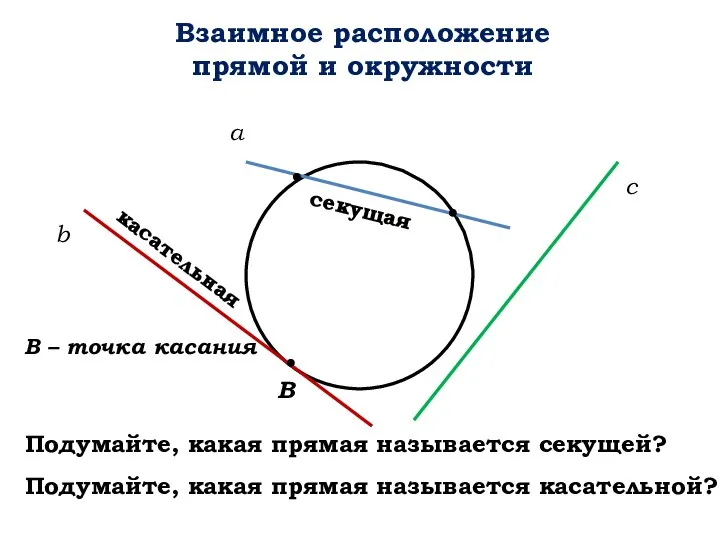 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Производная и первообразная
Производная и первообразная Презентация на тему ИСКУССТВО РАССУЖДАТЬ
Презентация на тему ИСКУССТВО РАССУЖДАТЬ  Презентация на тему Урок по теме «Координатная плоскость» 6 класс
Презентация на тему Урок по теме «Координатная плоскость» 6 класс  Отношения и золотое сечение
Отношения и золотое сечение Подготовка к ГИА. Алгебраические выражения. Часть 1
Подготовка к ГИА. Алгебраические выражения. Часть 1 Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Задачи на нахождение неизвестного слагаемого
Задачи на нахождение неизвестного слагаемого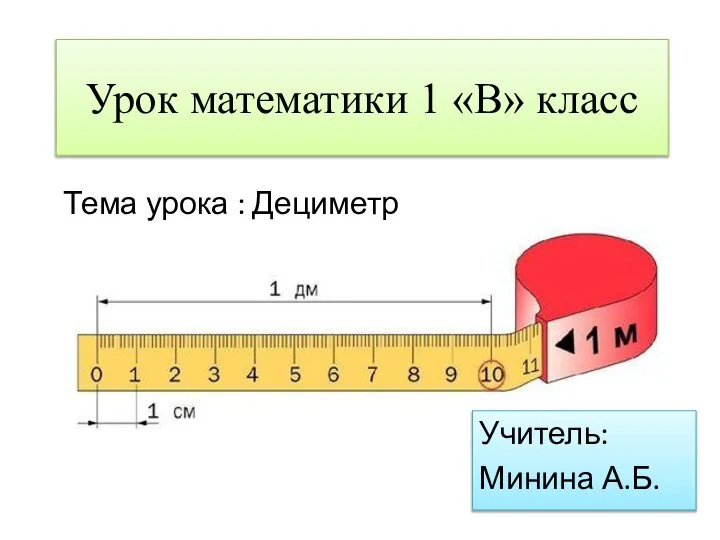 Дециметр
Дециметр Повторение. Математика, 1 класс
Повторение. Математика, 1 класс Элементы теории вероятности
Элементы теории вероятности Построение сечений многогранников
Построение сечений многогранников Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Задание 4. Числа, вычисления и алгебраические выражения
Задание 4. Числа, вычисления и алгебраические выражения Предел функции (часть 4)
Предел функции (часть 4)