Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения

Дифференциальные уравнения первого порядка
§ 1. Определение дифференциальных уравне-ний. Понятие решения дифференциального уравнения.
Определение 1. Уравнение вида
F(x, y(x), y′(x), …, y(n)(x)) = 0 (1)
Связывающее независимую переменную х, иско-мую функцию y(x) и ее производные называется обыкновенным дифференциальным уравнением.

Наличие хотя бы одной производной обязательно.
Определение 2. Функция y = ϕ(x), n раз дифференцируемая на (a,b) называется решением уравнения (1), если подстановка этой функции в уравнение (1) обращает его в тождество, т.е. F(x, ϕ(x), ϕ′(x), …, ϕ(n)(x)) ≡ 0.
Пример: y′′ + y = 0.
Его решение: y = sinx. Убедимся в этом:
y′ = cosx,
y′′ = - sinx,
Тогда:
- sinx + sinx ≡ 0.

Определение 3. Порядком дифференциального уравнения (1) называют порядок наивысшей производной , входящей в уравнение (1).
Пример: yIV + 3y′ + xy = cosx имеет четвертый порядок.
Определение 4. Дифференциальное уравнение вида (1) называется разрешенным относительно старшей производной, если оно может быть записано в виде:
y(n) = f (x, y(x), y′(x), y′′(x), …, y(n-1)(x)) (2)
Пример: y′ + x = 0.
Разрешим его относительно старшей производной:
y′ = - x.

Найдем первообразную:
y = - x2/2 + c.
Это выражение дает все решения дифференциального уравнения:
y′ + x = (- x2/2 + c)′ + x = - x + x = 0.
Определение 5. График решения дифференциального уравнения называется интегральной кривой.
Пример: для предыдущего примера, построим несколько интегральных кривых:

y = - x2/2 + c.
с = 2
с = 1
с = 0
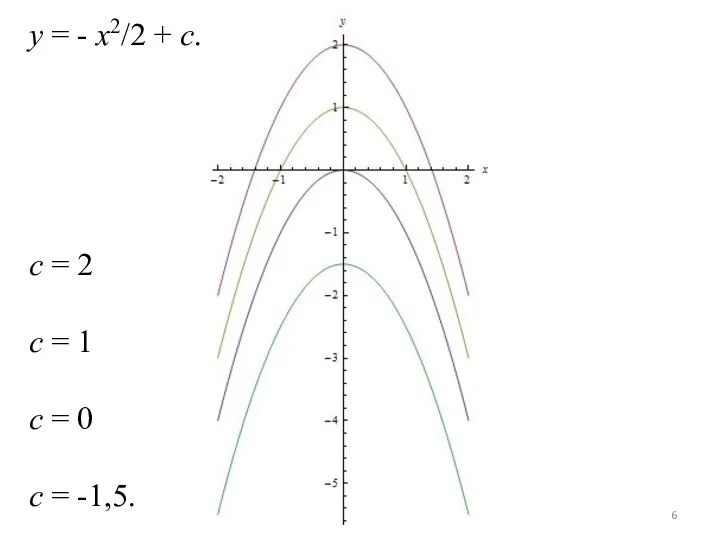
с = -1,5.

Для выделения из множества решений дифференциального уравнения единственного, ставится задача Коши.
Суть задачи Коши сводится к тому, чтобы найти решения дифференциального уравнения вида F(x, y(x), y′(x)) = 0, удовлетворяющему начальному условию:
y(x0) = y0 ⇔ y⏐x = x0 = y0.

Пример: Решить задачу Коши.
т.е. при условии, что y(1) = 1.
Решение.
Находим первообразную:
y = - x2/2 + c.
2) При помощи начального условия выделим решение задачи Коши:
Ответ:

Задача Коши не всегда имеет единственное решение. Единственное решение существует тогда и только тогда, когда выполняются условия теоремы:
Теорема (существования и единственности). Пусть в области D дано уравнение y′ = f (x,y). Если для точки M(x0,y0) существует окрестность, такая что:
1) f (x,y) непрерывна в ней по аргументам x и y.
2) частная производная ∂f/∂y ограничена по
абсолютной величине, т.е. . Тогда в этой
окрестности существует
единственное решение задачи Коши:

Геометрический смысл теоремы Коши.
Если выполняется условие теоремы в окрестности Ω точки M(x0,y0), то через точку M(x0,y0) проходит единственная в окрестности Ω интегральная кривая (см. рис.).
Теорема Коши – локальная теорема, если в окрестности Ω
существует
единственное
решение задачи
Коши, то вне
окрестности может
существовать 2 и
более решений.

Определение 6. Решение дифференциального уравнения, в каждой точке которого нарушается единственность называется особым решением дифференциального уравнения.
Обычно особое решение – это огибающая всех интегральных кривых дифференциального уравнения.
Общим решением для y′ = f (x,y) является
y = ϕ(x,c), такое, что: ϕ′ = f (x,ϕ(x,c)).
Если общее решение записано в виде Φ(x,y,c)=0, то выражение называется общим интегралом дифференциального уравнения.

§ 2. Типы дифференциальных уравнений первого порядка.
y′ = f (x) – простейший тип.
Решение его:
p(x)dx = q(y)dy дифференциальное уравнение с разделёнными переменными.
Если обозначить: P(x) и Q(y) так, что:
P′(x) = p(x), Q′(y) = q(y), то дифференциальное уравнение с разделенными переменными запи-шется в виде: dP = dQ, тогда: d(P – Q) = 0 ⇒
P – Q = c, при этом:

Пример: xdx = y2dy. Найти общий интеграл этого дифференциального уравнения.
Решение.
3x2 – 2y3 = 6c = c1*

§ 3. Дифференциальные уравнения с разделяющимися переменными.
Определение 7. Уравнение вида:
f1(x)ϕ1(y)dx = f2(x)ϕ2(y)dy (3)
или
y′x = f (x)ϕ(y) (4)
называется дифференциальным уравнением с разделяющимися переменными.
Очевидно, что (4) ⇒ (3), так как (домножим (4) на dx)
y′xdx = f (x)ϕ(y)dx, так как: y′xdx = dy, то:
dy = f (x)ϕ(y)dx.

Уравнение (3) сводится к уравнению с разделенными переменными.
Действительно. Разделим в (3) обе части на
f2(x)ϕ1(y) ≠ 0, тогда:
- уравнение с разделенными
переменными. Интегрируя, получаем:
Это выражение является общим интегралом дифференциального уравнения с разделенными переменными.

§ 4. Однородные дифференциальные уравнения первого порядка.
Предварительное замечание:
Определение 8. Функция f (x,y) называется однородной n-го измерения, если ∀p ≠ 0 имеет место f (px,py) = pnf (x,y).
В частности, если n = 0, то f (px,py) = f (x,y) – однородная функция нулевого измерения.
Теорема 1. Если P(x,y) и Q(x,y) – однородные функции одного измерения, то
однородная функция нулевого измерения.

Доказательство.
∀p ≠ 0 рассмотрим:
Ч.т.д.
Теорема 2. Однородная функция нулевого измерения зависит лишь от отношения переменных.
Доказательство.
Пусть f (px,py)=f (x,y) при ∀p≠0 рассмотрим
тогда:
Ч.т.д.

Определение 9. Уравнение вида
P(x,y)dx + Q(x,y)dy = 0 (5)
называется однородным дифференциальным уравнением первого порядка (в дифференциальной форме), где P(x,y) и Q(x,y) - однородные функции одного измерения.
Действительно. Разделим (5) на Q(x,y)dx ≠ 0, имеем:
Согласно теореме 1: - однородная

функция нулевого измерения и согласно теореме 2:
(6)
однородное дифференциальное уравнение первого порядка.
Однородные дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными путём введения новой функции:
Выразим y:
y = u(x)⋅x.

Продифференцируем его:
Подставим полученное выражение в (6):
В полученном уравнении легко разделяются переменные:
Получили уравнение с разделенными переменными, откуда:
Получили общее решение исходного уравнения, если ϕ(u) – u ≠ 0, x ≠ 0.

§ 5. Уравнения, приводящиеся к однородному.
1) Случай: если с = с1 = 0, то
Получили однородное уравнение.

2) Случай: если по крайней мере одно из чисел
с или с1 ≠ 0, и тогда путем
введения новых неизвестных:
x = X + h
y = Y + k,
где: h и k – решения системы:
данное уравнение сводится к однородному.

Покажем это:
dx = dX
dy = dY.
Подставим в исходное уравнение:
= 0
= 0
Получили однородное уравнение относительно неизвестной функции Y и:

3) Случай: если одно из чисел с или с1 ≠ 0, а
тогда ab1 = a1b ⇒ ⇒ a1 = ak и b1 = bk,
тогда:
путём введения новой функции
z(x) = ax + by
данное уравнение сводится к уравнению с разделяющимися переменными.

Покажем это:
Подставим все в исходное уравнение:
Получили общий интеграл.

§ 6. Линейные дифференциальные уравнения первого порядка.
Определение 10. Уравнение вида
+ P(x)y = Q(x) (7)
где P(x) и Q(x) - непрерывные функции, называется линейным дифференциальным уравнением первого порядка (относительно неизвестной функции y(x)).
Будем искать решение уравнения в виде произведения двух функций:

y(x) = u(x)⋅v(x)
где одну функцию можно взять произвольно с таким расчетом, чтобы уравнение упростилось, а вторую подобрать так, чтобы произведение этих двух функций являлось решением.
Найдем:
Подставим всё в (7):

Подберем функцию u так, чтобы:
Для этого в качестве u возьмем какое-либо решение уравнения:
Подставим полученное значение u в (*):

Общее решение:
y = u⋅v =
Замечание: Уравнение вида:
+ P(y)x = Q(y)
относительно x(y). Его решение ищется в виде:
x(y) = u(y)⋅v(y)

§ 7. Уравнение Бернулли.
Определение 11. Уравнение вида
+ P(x)y = Q(x)yα (8)
где P(x) и Q(x) - непрерывные функции и
α ≠ 0, α ≠ 1, называется уравнением Бернулли.
Уравнение Бернулли сводится к линейному: делим все члены уравнения на yα:
y-α + P(x)y1-α = Q(x) (**)