Алгоритм решения линейных уравнений

Самопроверка

Мы это знаем
Какие неравенства называются числовыми?
Изменится ли знак числового неравенства, если умножить или разделить обе части неравенства на положительное число?
Как изменится знак неравенства, если обе части умножить или разделить на отрицательное число?
Какие неравенства называются строгими, а какие нестрогими?
Какие неравенства называются двойными?

Вспомним

Алгоритм решения линейных уравнений
Раскрыть скобки, если они есть;
Перенести слагаемые, содержащие переменную, в одну сторону от знака равенства, а слагаемые без переменной — в другую;
Привести подобные слагаемые слева и справа от знака равенства;
Разделить обе части уравнения на коэффициент при переменной x

???

Линейные неравенства с одной переменной

Определение
Неравенства вида ax-b>0 или ax-b<0 называют линейными неравенствами с одной переменной,
где a и b некоторые числа,
х – переменная (неизвестная)

Решить неравенство – это значит найти множество его решений или
доказать, что их нет.

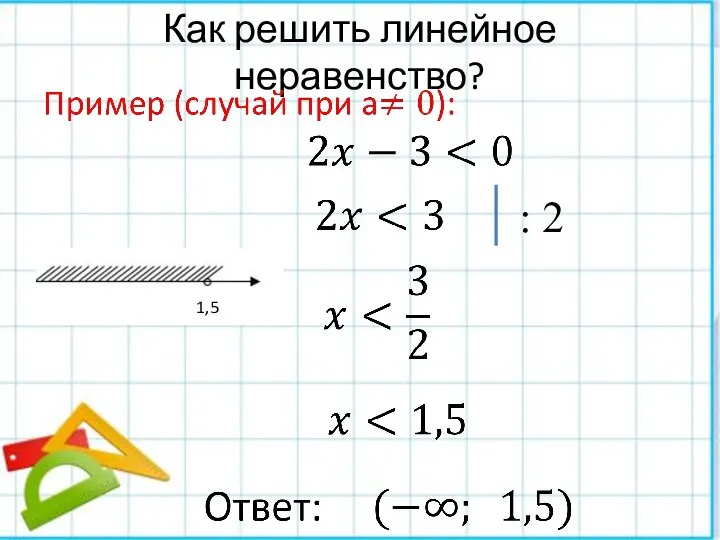
Как решить линейное неравенство?
: 2
1,5

Как решить линейное неравенство?
Неравенство не имеет решений

Алгоритм решения линейных неравенств
Раскрыть скобки, если они есть;
Перенести слагаемые, содержащие переменную, в одну сторону от знака неравенства, а слагаемые без переменной — в другую;
Привести подобные слагаемые слева и справа от знака неравенства;
Разделить обе части неравенства на коэффициент при переменной x.
В случае деления на отрицательное число, поменять знак неравенства на противоположный.

Решение упражнений на закрепление стр.204
№33.7(а,б)
33.9(а,б)
33.14(а,б)

Самостоятельная работа
1 вариант
(6;+∞)
(-∞;-1)
(-0,5;+∞)
2 вариант
[0,7;+∞)
[20;+∞)
[-1,4;+∞)

Кластер
Неравенства
Числовые промежутки
Числовые неравенства
Линейные неравенства
Строгие/нестрогие неравенства
Алгоритм решения линейных неравенств

Домашнее задание
№33.4
№33.5
№33.8