Слайд 2Область визначення функції
Область визначення - безліч, на якому задається функція. У кожній

точці цієї множини значення функції має бути визначено.
Слайд 3визначення
Якщо на множині {X} X задана функція, яка відображає безліч {X} X

в інше безліч, то безліч {X} X називається областю визначення або областю завдання функції.
Більш формально, якщо задана функція {f} f, яка відображає безліч {X} X в {Y} Y, тобто: {f \ X \ to Y} f \ X \ to Y, то безліч {\ X} X називається областю визначення
Слайд 4Область значень функції
Область значень (або безліч значень) функції - безліч, що складається

з усіх значень, які приймає функція
Слайд 5Визначення
Нехай на множині {X} X задана функція {f} f, яка відображає безліч

{X} X в {Y} Y, тобто: {X to Y} f: X to Y. Тоді областю (або безліччю) значень функції { f} f називається сукупність всіх її значень, яка є підмножиною множини
Слайд 6Парність і непарність функції
Функцію y=f(x), x ∈ X називають парною, якщо для будь-якого

значення x із множини X виконується рівність f ( − x ) = f ( x ) . Функцію y=f(x), x ∈ X називають непарною, якщо для будь-якого значення x із множини X виконується рівність f ( − x ) = − f ( x ) .
Слайд 7Визначення
Функція y = f (x) є парною, якщо для будь-якого значення x∈X

виконується рівність: f (-x) = f (x). Область визначення парної функції повинна бути симетрична щодо нуля. Якщо точка b належить області визначення парної функції, то точка -b також належить даній області визначення. Графік парної функції також буде симетричний щодо центру координат.
Непарній називається функція y = f (x) за умови виконання рівності f (-x) = - f (x). Графік функції непарної функції, на відміну від парної, симетричний щодо осі координат. Якщо точка b належить області визначення непарної функції, то точка -b також належить області визначення цієї функції.






 Геометрия в живописи
Геометрия в живописи Теория вероятностей
Теория вероятностей Условный оператор задач
Условный оператор задач Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Время. Решение задач
Время. Решение задач Математика вокруг нас
Математика вокруг нас Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен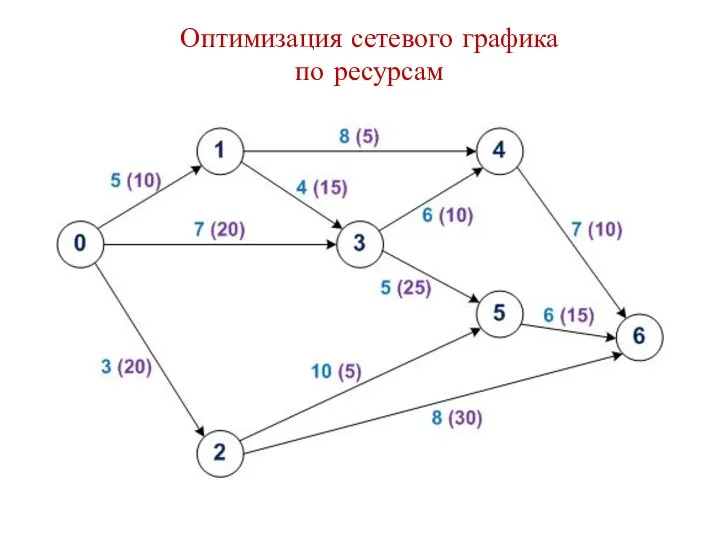 Оптимизация сетевого графика по ресурсам
Оптимизация сетевого графика по ресурсам Построение сечений
Построение сечений Тела вращения. Использование ИКТ
Тела вращения. Использование ИКТ МЕТОДИКА ИСПОЛЬЗОВАНИЯ ДИДАКТИЧЕСКИХ ИГР НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
МЕТОДИКА ИСПОЛЬЗОВАНИЯ ДИДАКТИЧЕСКИХ ИГР НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ Ломаная линия. Обозначение ломаной
Ломаная линия. Обозначение ломаной Таблица значений синуса, косинуса, тангенса для углов
Таблица значений синуса, косинуса, тангенса для углов Арифметическая прогрессия
Арифметическая прогрессия Задания Незнайки
Задания Незнайки Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ»
Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ» Делимость чисел. НОК
Делимость чисел. НОК Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи Презентация на тему Длина окружности и площадь круга (9 класс)
Презентация на тему Длина окружности и площадь круга (9 класс)  Параллельный перенос
Параллельный перенос Действия с дробями. Устная работа
Действия с дробями. Устная работа Первый признак параллельности прямых
Первый признак параллельности прямых Презентация на тему Перестановка слагаемых (1 класс)
Презентация на тему Перестановка слагаемых (1 класс)  Натуральные числа и их обозначение
Натуральные числа и их обозначение Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Это полезно знать
Это полезно знать Выражение отношения в процентах
Выражение отношения в процентах Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс