Объём. Начало геометрии

Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI - V вв. до н. э. в Древней Греции в геометрии начался новый этап развития, что объясняется высоким уровнем, которого достигла общественно-политическая и культурная жизнь в греческих государствах.

В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для определения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды. Определять объем призмы, пирамиды, цилиндра и конуса умели древние греки и до Архимеда. И только он нашел общий метод, позволяющий определить любую площадь или объем.

Идеи Архимеда легли в основу интегрального исчисления. Сам Архимед определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. Он вывел, что объем шара, составляет две трети от объема описанного около него цилиндра. Он считал это открытие самым большим своим достижением. Среди замечательных греческих ученых V - IV вв. до н.э., которые разрабатывали теорию объемов, были Демокрит и Евдокс Книдский.

Еще в детском саду, развивая количественные представления учащихся, дети учились измерять количество сыпучих и жидких веществ ложками, формочками, выясняли, в какую формочку песка входит меньше (больше).
В 1 классе эта работа продолжается: учащиеся сравнивают емкость или вместимость различных сосудов. Вначале сравнение проводится на глаз (сосуды значительно отличаются по своей емкости). Например, предлагается сравнить, куда войдет воды больше: в банку или в кастрюлю. Перед учащимися ставятся пол-литровая банка и кастрюля емкостью 2-3 л, измеряется, сколько банок воды входит в кастрюлю.
Тема "Литр" изучается в концентре "Десяток" (1 класс).

Выявляя имеющийся у учащихся опыт, учитель предъявляет и стандартные банки вместимостью 1 л, 2 л, 3 л. Многие ребята знают вместимость этих банок, некоторые же не имеют о ней никакого представления. Учитель выясняет также, знают ли учащиеся, какими мерами измеряют объем молока, бензина, растительного масла, вообще жидкости. Затем он показывает детям литровую кружку, бутылку, банку, наливает воду в кружку, а затем поочередно переливает воду из нее в бутылку и банку. Так учащиеся подводятся к выводу, что в банку вмещается столько же воды, сколько в кружку, и столько же, сколько в бутылку, т.е. равное, одинаковое количество воды – 1 л.

Чтобы этот вывод был понятен учащимся, необходимо, чтобы каждый ученик проделал эту несложную работу сам. Важно, чтобы дети запомнили это новое слово, научились правильно его произносить и записывать при числах. Учащиеся должны уметь отыскивать среди других сосудов сосуд емкостью 1 л.

Далее учащиеся учатся измерять вместимость сосудов и отмеривать заданное количество литров. Они определяют, наполняя водой, емкость банок, небольших бидонов, кастрюль, ведер. Важно развивать глазомер учащихся, т. е. умение определять емкость сосудов на глаз. Они должны запомнить емкость стандартных, наиболее часто встречающихся в быту сосудов: банки емкостью 0,5 л, 1 л, 2 л, 3 л, 5 л, бидоны емкостью 1 л, 2 л, 3 л, 5 л, 10 л, 20 л, 40 л, ведра емкостью 8л, 10л, 12 л

Объем — это вместимость геометрического тела, т. е. части пространства, ограниченной одной или несколькими замкнутыми поверхностями. Вместимость или емкость выражается числом заключающихся в объеме кубических единиц.

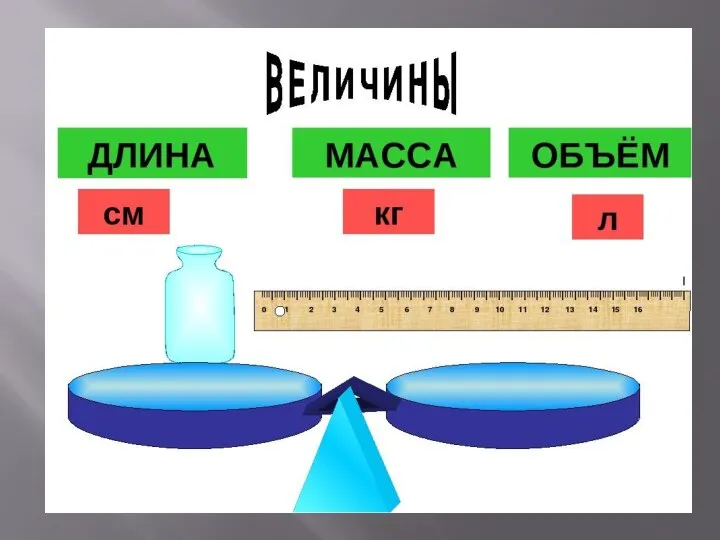
В математике основными понятиями являются понятия «число и величина». Под величиной понимают некоторые свойства предметов и явлений, которые связаны с измерениями. В начальных классах знакомят с пятью основными величинами : длиной, площадью, массой, объёмом , временем

Ученики должны научиться сравнивать предметы с точки зрения величин, измерять величины используя различные измерительные приборы и единицы измерения . У учеников формируется правильная математическая речь . Нельзя сказать , что 17 см – это число , это величина , но 17 – это числовое значение величины. Оно зависит от того в какой единицей измерения пользовались . Чем больше единицы измерения , тем меньше числовое значение величины : 7 000 метров или 7 км.

В методике выделяют следующие этапы изучения этих величин:
1- Ознакомление с величиной, на основе уточнения жизненных представлений учащихся
2- Сравнение величин разными способами
А – С помощью ощущений или на глаз
Б - С помощью приемов наложения или приложения
В - С помощью различных мерок

3- Введения единой меры измерения и измерительного прибора, формирование измерительных навыков
4- Сложение и вычитание величин, выраженных в одной единицы измерения
5- Введение других единиц измерения величины. Перевод из одной единицы измерения в другую
6- Сложение и вычитание величин, выраженных в единицы двух наименований
7- Умножение и деление величины на число

Пользуясь этим подходом, рассмотрим методику изучения такой величины как объём или емкость.

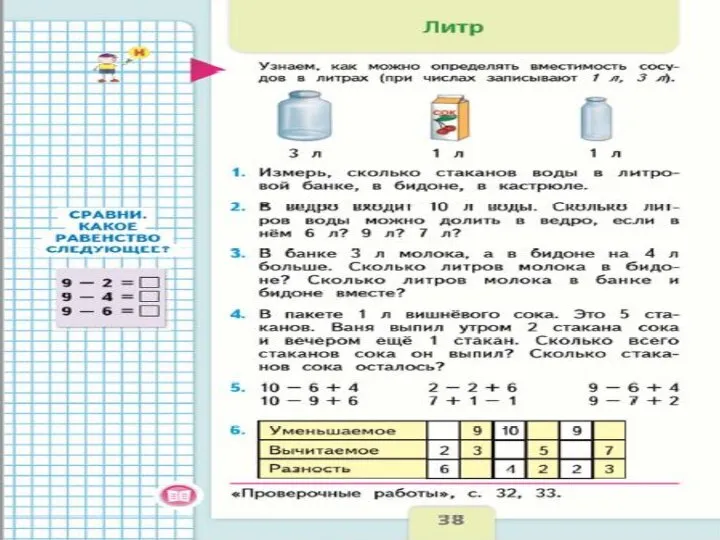
С этой величиной детей знакомят по- разному в разных программах. Так по программе М.И. Моро термин объём не вводят, а используют понятие «ёмкость сосуда»

1. Введение понятия с опорой на жизненные ситуации.
Учитель приносит на урок различные сосуды : стакан, ведро , банку . Дети сравнивают их и при сравнении размера , учитель сообщает , что в математике, говоря о размере сосудов, мы подразумеваем ёмкость. Например, ёмкость одного сосуда меньше ( больше, равна) ёмкости другого сосуда. М1М ч 2. стр. 38.

2. Сравнение сосудов по ёмкости разными способами.
А) « на глаз» Показываем сосуды, контрастные по объему (стакан и ведро…). Учим правильно формулировать вывод.
Б) переливанием в другой сосуд. На столе широкий, но низкий сосуд и высокий, но узкий. В них жидкость : ёмкость какого сосуда больше? После дискуссии переливаем по очереди жидкость из каждого сосуда в третий сосуд-посредник и ставим отметку, затем сравниваем отметки и делаем вывод.

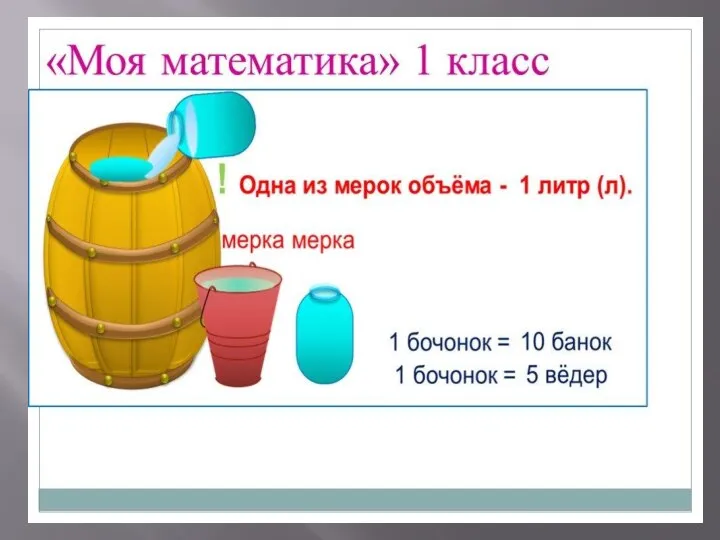
В) Использование мерок. Ещё в детском саду детей знакомят с этим
Способом. В качестве мерок используют маленькие чашечки .Проводим несколько опытов измерения емкости различными мерками. Например, емкость банки равна 4 чашкам.
Показываем на примере, что в жизни неудобно использовать разные мерки, нужна единая мера.
3. Введение единой меры емкости.
Вводят литр. Показываем литровую банку и затем проводим практическую работу по определению ёмкости сосудов в литрах ( например, 3л, 5л, 7 л) , Для этого приносят такие сосуды в класс ( банки, ведра…). Практически доказываем, что 5 стаканов составляют 1 литр.

4.Сложение и вычитание величин, выраженных в литрах.
Решают задачи.
Например: В банке 3 л молока, а в ведре на 4 л больше. Сколько в ведре?

По некоторым программам ( Н.Б.Истоминой, И.И. Аргинской и т.д.) детей знакомят с понятием « Объём фигур» и рассматривают трёхмерные геометрические фигуры. Берут куб и прямоугольный параллелепипед. Анализируя куб и прямоугольный параллелепипед , говорят о единицах измерения объема

Изучение геометрических фигур начинается со знакомства с точкой и линией и рассмотрения их взаимного расположения. Сравнение разных видов линий приводит к появлению различных многоугольников, а затем - к знакомству с пространственными фигурами. Геометрические величины (длина, площадь, объем) изучаются на основе единого алгоритма, базирующегося на сравнении объектов и применении различных мерок. Умение строить различные геометрические фигуры и развертки пространственных фигур, находить площади и объемы этих фигур необходимо при выполнении различных поделок на уроках технологии, а также в жизни.

Изучение линии величин завершается в 4 классе составлением таблиц мер изученных величин и соотношений между ними, а также сравнением этих таблиц между собой и с десятичной системой счисления.

По программе Аргинской И.И. кроме этого выводят правило нахождения объёма куба и прямоугольного параллелепипеда : М4А ч.2 с.26.
V = a ∙b ∙c Для вывода этого правила рассматриваем модель прямоугольного параллелепипеда . Можно её сложить из кубиков, принимая , что 1 кубик = 1 единице объёма, например 1 дм3. Например,
прямоугольный параллелепипед размером 3х4х5.

Например. Сколько всего кубиков в моделе, т. е. сколько единиц измерения объёма, в этом прямоугольном параллелепипеде? Сначала подсчитываем , сколько кубиков потребуется для одного уровня . Дети умеют находить S прямоугольника , следовательно ,ответят 3∙4 =12 . Уточняем , что обозначают числа 3 и 4? Это числовое значение длины и ширины. Таких уровней в нашем параллелепипеде 5 , следовательно , всего 3∙4∙5 кубиков, где 5 – это числовое значение высоты , следовательно,
V параллелепипеда = произведению длины, ширины и высоты.

Изучение таких величин, как длина, масса, время, площадь, и действий с ними также проходит через всю начальную школу и завершается в 4 классе анализом соотношений между разными единицами измерения одной и той же величины. Такой анализ помогает ученикам осознать их связь с десятичной системой счисления (или отсутствие такой связи, как, например, таблицы соотношения единиц измерения времени).

Л. Г. Петерсон уделяет довольно большое внимание геометрическому материалу в своей программе по математике. В общих целях изучения математики она среди прочих выделяет следующую цель: познакомить с простейшими геометрическими формами, научить распознавать, называть и изображать геометрические фигуры, сформировать условия для овладения способами измерения длин и площадей. Из этого видно, что довольно много внимания она уделяет развитию геометрических навыков, много места в содержании программы она уделяет геометрическому материалу.

В течение первых десяти уроков третьей части учебника «Математика–1» учащиеся знакомятся с величинами: длина, масса, объем.

Цель урока: сформировать представление об объеме (вместимости) тела; выявить зависимость между результатом измерения объема и величиной мерки; познакомить с различными единицами измерения объема и эталоном – литр. К этому уроку надо подготовить различные сосуды для измерения соответствующие мерки − стаканчики, чашки, кружки. Для эффективного усвоения детьми данного понятия необходимо организовать практическую работу каждого ребенка по непосредственному сравнению объемов сосудов и их измерению. Изучению величины «объем» должно предшествовать повторение основных сведений о величинах и их измерении, с которыми учащиеся познакомились на предыдущих уроках. Затем изучение объема проводится по тому же плану, что и изучение других величин.

В конце урока учащиеся должны назвать следующие шаги измерения объема сосудов:
1) Выбрать мерку (единицу измерения).2) Узнать, сколько таких мерок содержится в измеряемом сосуде.

Полученное число и есть результат измерения объема данного сосуда выбранной меркой. Другими словами, чтобы измерить объем предмета, надо выбрать мерку (единицу измерения) и узнать, сколько мерок содержится в этом сосуде. Далее учитель сообщает учащимся, что первоначальные древние меры объема (вместимости) жидкости – бочка и ведро. Древней мерой зерна была кадь, она делилась на 2 половника, или 4 четверти, или 8 осьмин. В разных местностях эти меры значительно отличались друг от друга. Например, московская кадь была примерно в полтора раза больше киевской. Потребности практики, как и в случае измерения других величин, привели к появлению единой системы мер. Одной из общепринятых современных единиц измерения объемов жидких и сыпучих веществ является литр.

В завершение урока еще раз систематизируются и проговариваются выводы, полученные на данном уроке:
· Объем (вместимость) является величиной – он характеризует вместимость сосудов, больше или меньше жидкости или сыпучих тел в них войдет.
· Чтобы измерить объем сосуда, нужно выбрать мерку и узнать, сколько таких мерок содержится в этом сосуде.
· С увеличением мерки значение объема уменьшается, и наоборот. Поэтому сравнивать, складывать и вычитать объемы можно только тогда, когда они измерены одной и той же меркой.
· Древние единицы объема были не всегда точны. Сейчас в качестве мерок в основном используются единые единицы измерения объема (эталоны). Одной из них является литр.