Содержание
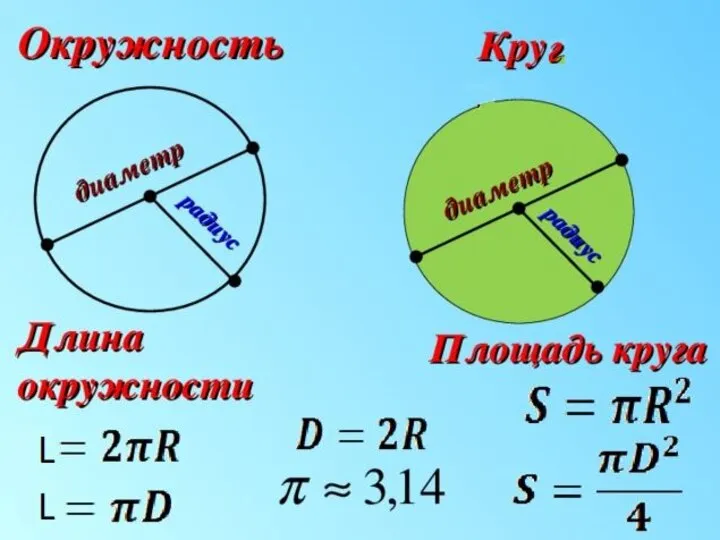
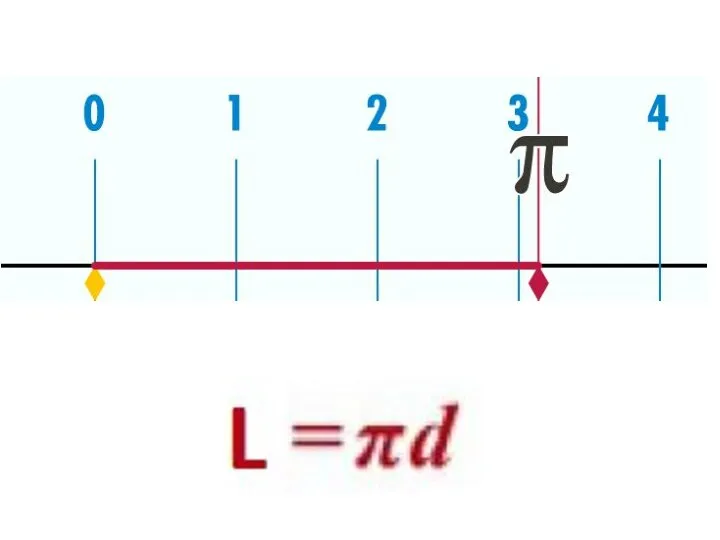
- 3. Окружность – это замкнутая линия, каждая точка которой находится на одинаковом расстоянии от центра. Круг –
- 5. Задание 1
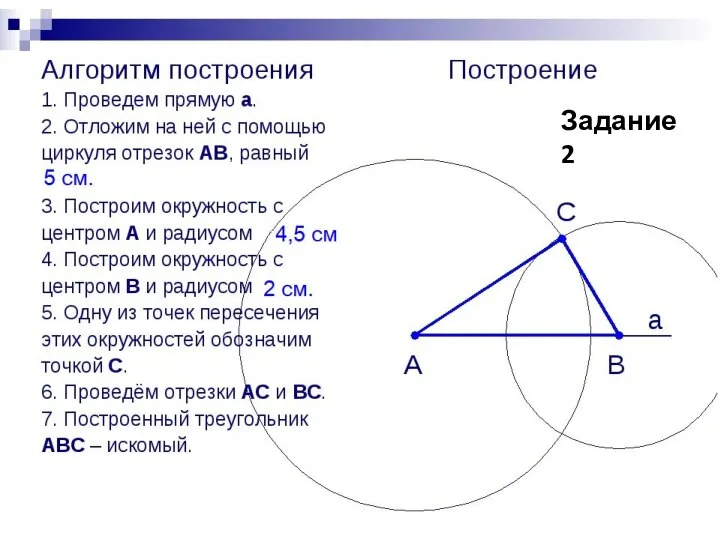
- 6. Задание 2
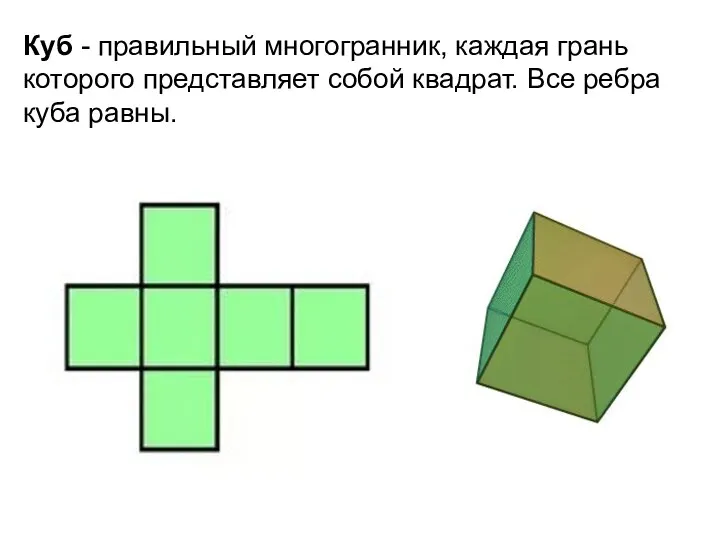
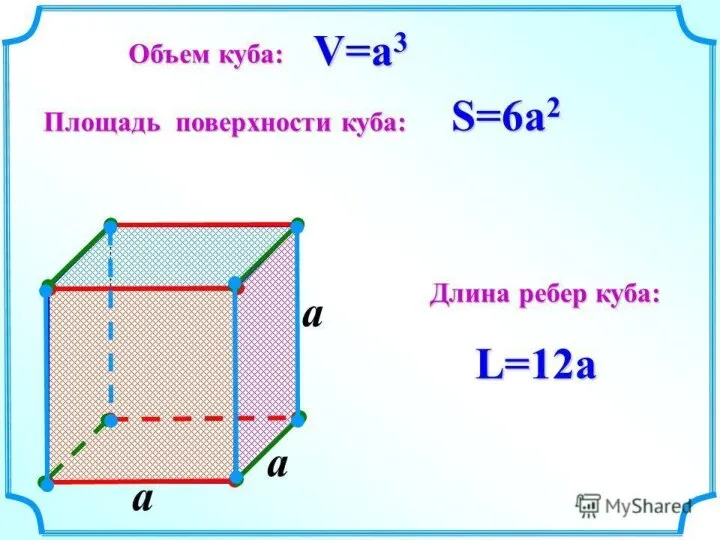
- 7. Куб - правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
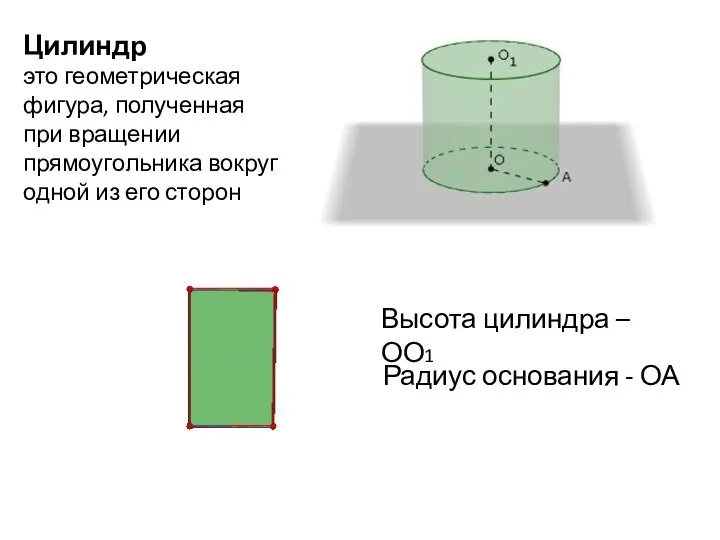
- 9. Цилиндр это геометрическая фигура, полученная при вращении прямоугольника вокруг одной из его сторон Высота цилиндра –
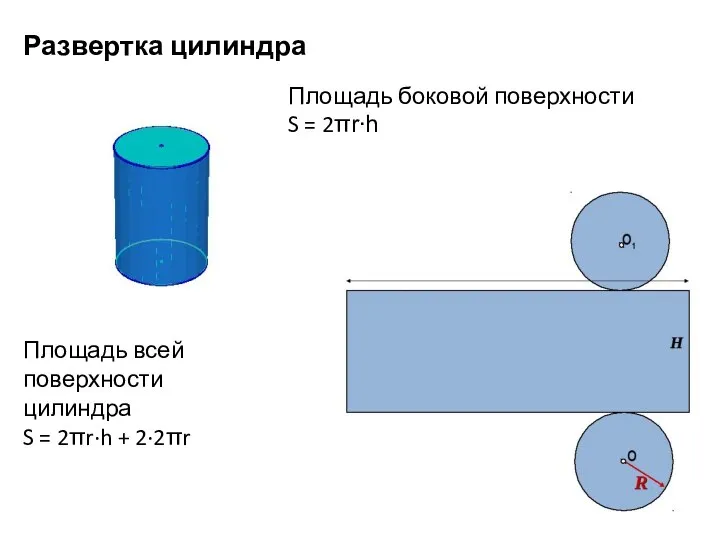
- 10. Развертка цилиндра Площадь боковой поверхности S = 2πr∙h Площадь всей поверхности цилиндра S = 2πr∙h +
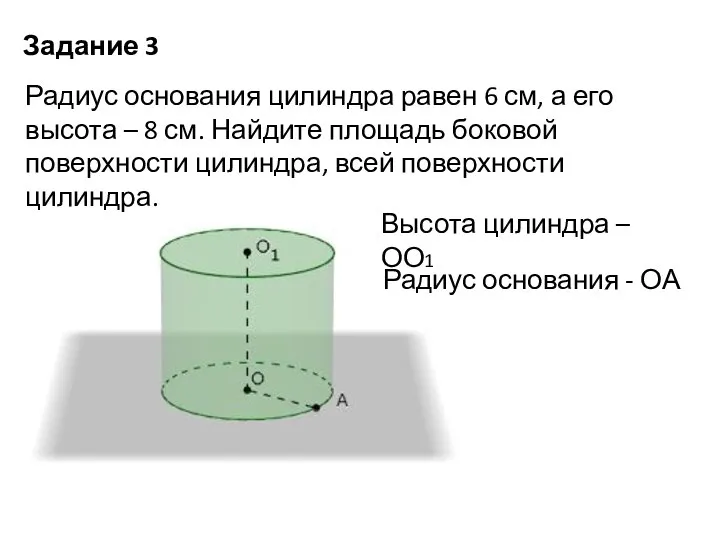
- 11. Задание 3 Радиус основания цилиндра равен 6 см, а его высота – 8 см. Найдите площадь
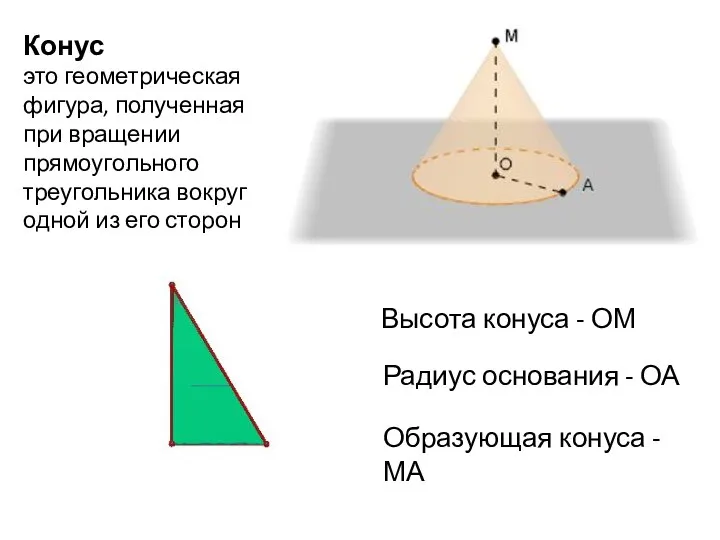
- 12. Конус это геометрическая фигура, полученная при вращении прямоугольного треугольника вокруг одной из его сторон Высота конуса
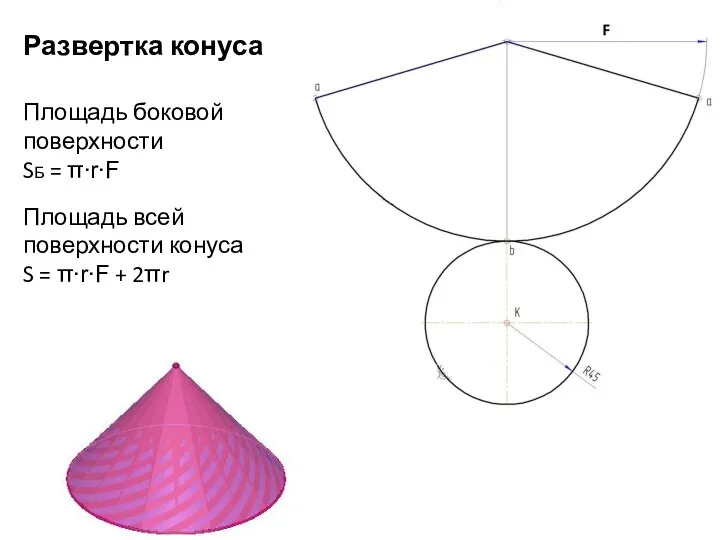
- 13. Развертка конуса Площадь боковой поверхности SБ = π∙r∙F Площадь всей поверхности конуса S = π∙r∙F +
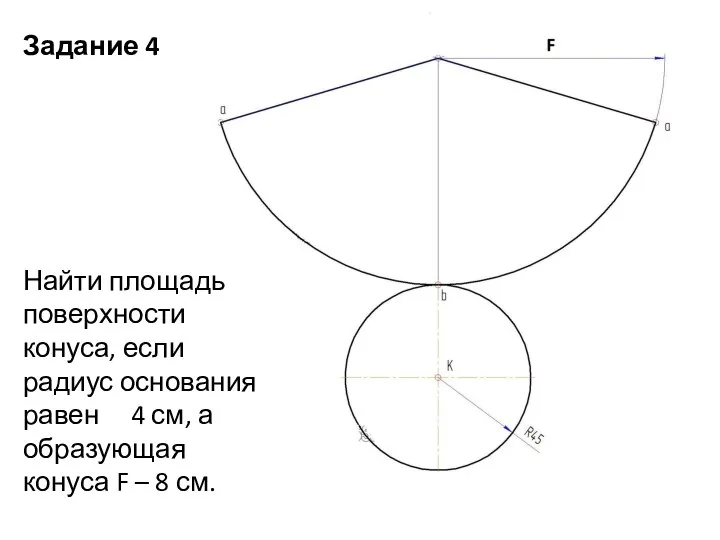
- 14. Задание 4 Найти площадь поверхности конуса, если радиус основания равен 4 см, а образующая конуса F
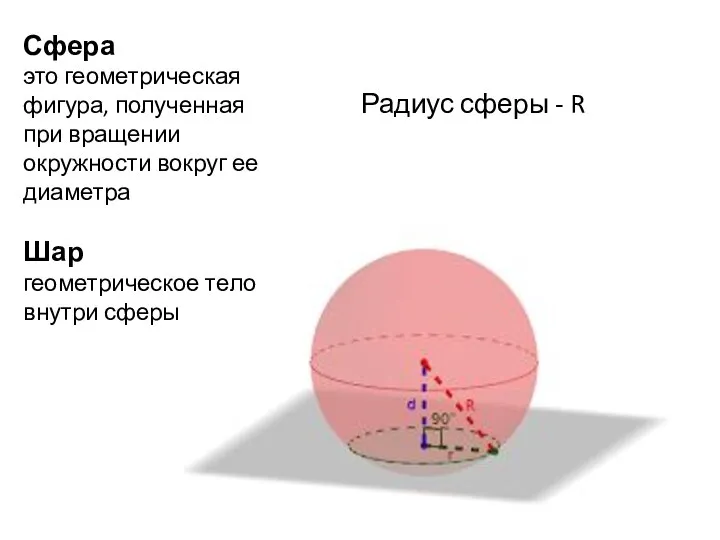
- 15. Сфера это геометрическая фигура, полученная при вращении окружности вокруг ее диаметра Шар геометрическое тело внутри сферы
- 17. Скачать презентацию


 Метод Лагранжа решения ЛНДУ
Метод Лагранжа решения ЛНДУ Шар и сфера
Шар и сфера Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Урок 23
Урок 23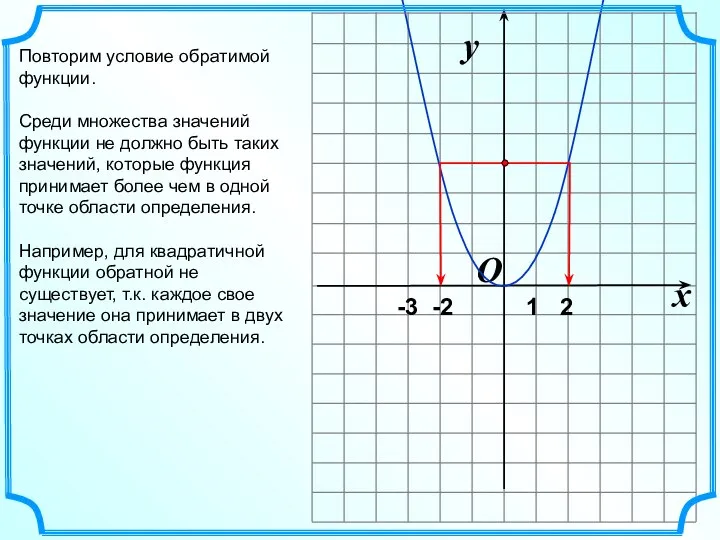 Арксинус
Арксинус Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Векторы в пространстве
Векторы в пространстве Задачи на готовых чертежах
Задачи на готовых чертежах Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Замена переменных в двойных интегралах
Замена переменных в двойных интегралах Функции. Свойства функций. Математический анализ
Функции. Свойства функций. Математический анализ Четырехугольники
Четырехугольники Противоположные числа. Устный счет
Противоположные числа. Устный счет В мире треугольников
В мире треугольников Диаграммы и графики. 6 класс
Диаграммы и графики. 6 класс Квадрат та його властивості
Квадрат та його властивості Плоскость и прямая в пространстве
Плоскость и прямая в пространстве Число 6 в стране геометрических фигур
Число 6 в стране геометрических фигур 9_setyabrya_distant_urok_matem (1)
9_setyabrya_distant_urok_matem (1) Логические операции. Конъюнкция, дизъюнкция, отрицание, импликация, эквивалентность
Логические операции. Конъюнкция, дизъюнкция, отрицание, импликация, эквивалентность Сложение и вычитание положительных десятичных дробей
Сложение и вычитание положительных десятичных дробей Предельный переход в неравенствах
Предельный переход в неравенствах Решение текстовых задач
Решение текстовых задач Образец решения уравнения х2=а
Образец решения уравнения х2=а Приёмы устных вычислений вида 260+310, 670-140
Приёмы устных вычислений вида 260+310, 670-140 Физико-математический турнир. Интегрированный урок
Физико-математический турнир. Интегрированный урок Решение уравнений «В мире звезд»
Решение уравнений «В мире звезд»