Содержание
- 2. План Определение, порядок определителя Миноры и алгебраические дополнения Свойства определителей Вычисление определителей: итоги Понятие обратной матрицы.
- 3. Из истории науки Швейцарский математик Крамер (G. Cramer, 1704–1752) заложил основы теории определителей, хотя и не
- 4. Габриэль Крамер Gabriel Cramer 1704–1752 Швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной
- 5. Определитель (или детерминант) — одно из основных понятий линейной алгебры Это многочлен, комбинирующий элементы квадратной матрицы
- 6. специальные виды определителей Определитель Вронского (Вронскиан) Определитель Вандермонда Определитель Грама Определитель Якоби (Якобиан) Циркулянт
- 7. 1. Определение. порядок определителя Определение. ОПРЕДЕЛИТЕЛЬ (детерминант) n-го порядка, составленный из элементов квадратной матрицы (n*n) есть
- 8. Для обозначения определителя квадратной матрицы используется символ: т.е. элементы матрицы заключаются в прямые вертикальные чёрточки. Определитель
- 9. Определители второго порядка. Определение: Определителем или детерминантом второго порядка называется ЧИСЛО Числа (элементы определителя) a11 и
- 10. Правило: Чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведения элементов побочной
- 11. Определители третьего порядка. Определение: Определителем или детерминантом третьего порядка называется ЧИСЛО
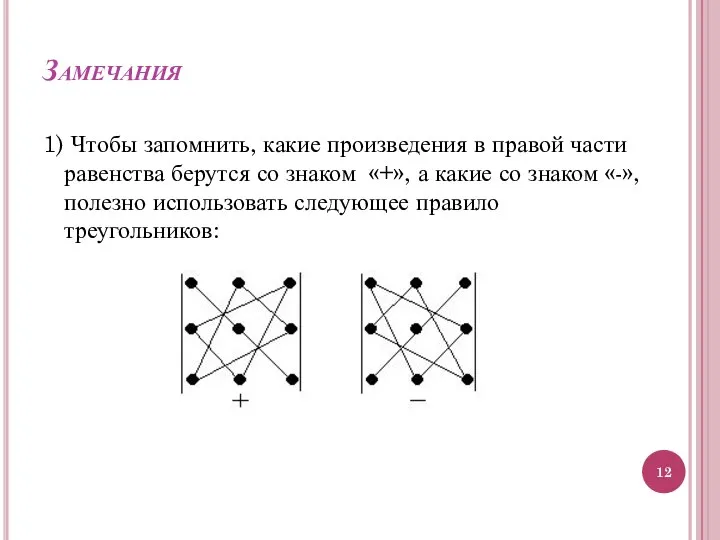
- 12. Замечания 1) Чтобы запомнить, какие произведения в правой части равенства берутся со знаком «+», а какие
- 13. 2) Второй способ вычисления определителя фактически совпадает с первым и называется способом Саррюса Суть его состоит
- 14. 3) Определитель 4-го порядка есть алгебраическая сумма 4!=4*3*2*1=24 слагаемых! Как вычисляются определители, имеющие порядок выше 3-го?
- 15. Пример. Вычислить определитель с помощью правила (способа)Саррюса. Решение
- 16. 2. Миноры и алгебраические дополнения Определение: Минором некоторого элемента называется определитель, который получается из данного определителя
- 17. Минор элемента есть ОПРЕДЕЛИТЕЛЬ 2-ГО ПОРЯДКА, который получается путём зачёркивания 1-й строки и 1-го столбца исходного
- 18. 2) Вычислить миноры и определителя Решение
- 19. Определение: Алгебраическим дополнением какого-либо элемента определителя есть минор этого элемента, взятый со знаком : Пример. Для
- 20. Решение Дан определитель Согласно определению находим
- 21. Замечание Алгебраическое дополнение элемента совпадает с его минором , если сумма его индексов i+j чётна, и
- 22. 3. Свойства определителей Определитель обладает рядом свойств, которые лежат в основе практических способов их вычислений Время,
- 23. 1. Величина определителя не изменится, если его строки и столбцы поменять местами: Для доказательства используем определение
- 24. 3. Умножение всех элементов одного столбца или одной строки определителя на любое число λ равносильно умножению
- 25. 5. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель
- 26. 7. Если каждый элемент некоторого столбца (строки) определителя представляет собой сумму двух слагаемых, то определитель может
- 27. 8. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженный на
- 28. 9. Определитель равен сумме произведений элементов какого-нибудь столбца или строки на их алгебраические дополнения 10. Сумма
- 29. Какие свойства определителей полезно знать? 1) Величина определителя не меняется при транспонировании. Свойство запоминаем. 2) Любая
- 30. Пример. Вычислить определитель, используя свойство 9.
- 31. Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где: 1) нулей побольше 2) числа поменьше 3) использовать
- 32. Решение 1. Выбираем строку или столбец: это третий столбец 2. Записываем формулу вычисления определителя
- 33. Замечание Можно упростить запись, если использовать правило знаков:
- 34. 4. Вычисление определителей (итоги) 1. Значение определителя второго порядка находим по определению: 2. Определитель третьего порядка
- 35. 4. Если в определителе все числа, расположенные ниже или выше главной диагонали, или все числа кроме
- 36. 5. ОПРЕДЕЛИТЕЛЬ РАВЕН НУЛЮ, если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы) Пример.
- 37. 5. Понятие обратной матрицы Определение: Если A – КВАДРАТНАЯ НЕВЫРОЖДЕННАЯ МАТРИЦА, то обратной для нее называется
- 38. Обратная матрица определяется единственным образом по формуле Здесь транспонированная матрица алгебраических дополнений соответствующих элементов исходной матрицы
- 39. Алгоритм построения (нахождения) обратной матрицы 1. Убедиться, что исходная матрицы не является вырожденной, т.е. убедиться, что
- 40. 4. Записать обратную матрицу 5. Проверить правильность решения, т.е. убедиться, что выполняется равенство: или
- 41. 6. Матричные выражения Матричное выражение состоит из матриц, связанных операциями сложения, умножения, возведения в степень, транспонирования
- 42. Матричные уравнения Матричное равенство, содержащее неизвестную матрицу, называется матричным уравнением Например, простейшие из них вида
- 43. Замечание Выполнены все требования, предъявляемые к размерам матриц, входящих в матричные уравнения Решить матричное уравнение –
- 44. Рассмотрим решение матричного уравнения вида Решение
- 45. Пример. Решить уравнение Решение Задано уравнение вида После умножения СПРАВА это уравнение на матрицу получаем, что
- 46. Вычислим определитель матрицы A: Найдём миноры и алгебраические дополнения матрицы A: Составим обратную матрицу
- 47. 2. Найдём неизвестную матрицу : 3. Проверка
- 50. Скачать презентацию












































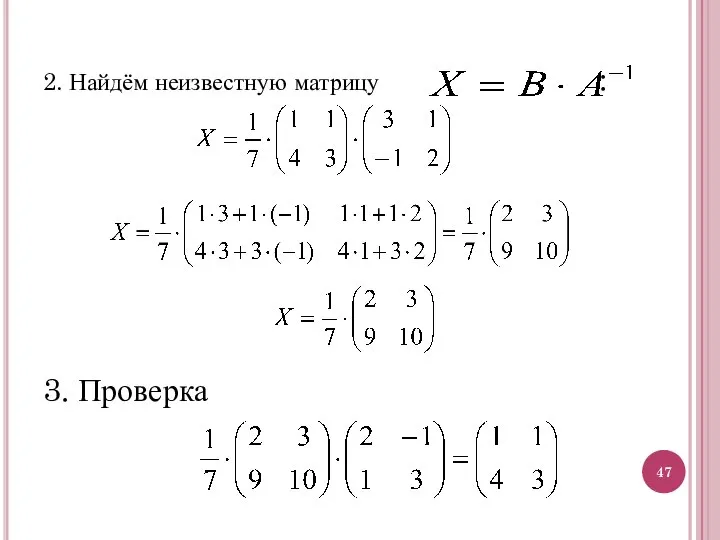

 Пперпендикулярные прямые
Пперпендикулярные прямые Решение текстовых задач с помощью уравнений
Решение текстовых задач с помощью уравнений Логические операции
Логические операции Задачи на кратное сравнение
Задачи на кратное сравнение Связь суммы со слагаемыми
Связь суммы со слагаемыми Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Основные понятия и определения метрологии. Лекция 1
Основные понятия и определения метрологии. Лекция 1 Математическая викторина. 2 тур. Великие и знаменитые
Математическая викторина. 2 тур. Великие и знаменитые Сократите дробь решите систему, уравнение, упростите выражение и т.д
Сократите дробь решите систему, уравнение, упростите выражение и т.д Показательная функция и ее применение
Показательная функция и ее применение Таблицы. Алгебра 7 класс
Таблицы. Алгебра 7 класс Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Перпендикуляр и наклонная
Перпендикуляр и наклонная Математическое моделирование
Математическое моделирование Арифметическая прогрессия. Всё в твоих руках
Арифметическая прогрессия. Всё в твоих руках ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел»
ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел» 3_Equations_2
3_Equations_2 Выражения с переменными
Выражения с переменными Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Методика изучения геометрического материала
Методика изучения геометрического материала Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Задачи на нахождение неизвестного по двум разностям
Задачи на нахождение неизвестного по двум разностям Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Формулы тангенсов и котангенсов
Формулы тангенсов и котангенсов Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Умножение обыкновенных дробей
Умножение обыкновенных дробей