Определённый интеграл

Свойства определенного интеграла
Для произвольных чисел a, b, c справедливо равенство:
Если f(x) ≤ ϕ(x) на отрезке [a, b] a < b, то

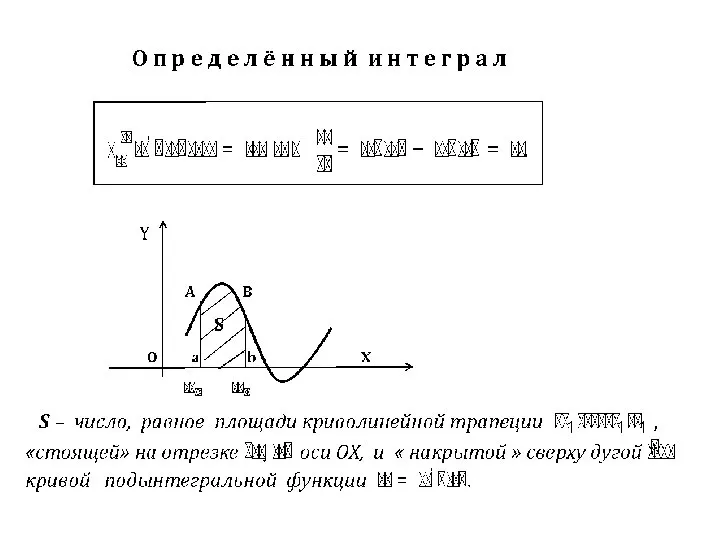
Формула Ньютона – Лейбница
Пример

Формула интегрирования по частям для определенного интеграла
Пример

Тема 4. Приложения определённого интеграла в геометрии.
1. Вычисление длины дуги плоской кривой.

Вычисление длины дуги плоской кривой,
заданно в декартовых координатах.
П р и м е р 1. Вычислить длину дуги полукубической параболы

П р и м е р 2. Вычислить длину дуги астроиды
Р е ш е н и е.
Вычисление длины дуги плоской кривой,
заданной параметрически .

Вычислить длину дуги кривой в полярных координатах
Р е ш е н и е.

2. Вычисление площадей плоских фигур.

П р и м е р .

П р и м е р . Вычислить площадь фигуры, ограниченной кривой, заданной в полярных координатах уравнением
(см. рис.)
Р е ш е н и е.