Оптимизационные задачи

Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.
Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

Классификация задач оптимизации
* Последний тип задач является самым сложным и требует точного составления оптимизационной модели.

Параметрическая оптимизация
Постановка задачи:
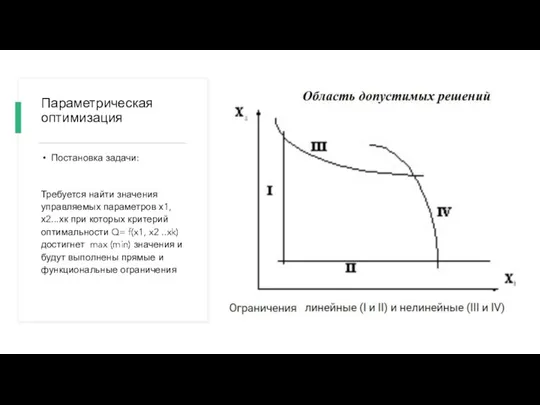
Требуется найти значения управляемых параметров х1,х2...хк при которых критерий оптимальности Q= f(x1, x2 ..xk) достигнет max (min) значения и будут выполнены прямые и функциональные ограничения

Структура оптимизационной модели
Целевая функция (критерий оптимальности)
состоит из управляемых переменных;
неуправляемых переменных;
формы функции (вида зависимости между ними).
Область допустимых решений
область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Постановка задачи оптимизации

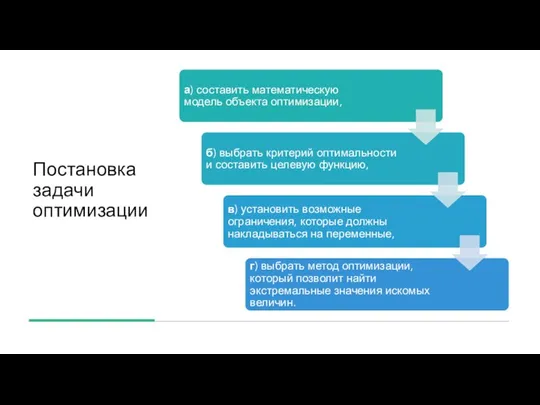
Задачи оптимизации различают:
В зависимости от управляемых параметров:
одномерная оптимизация (оптимизация 1 параметра),
двухмерная/многомерная оптимизация (оптимизация 2 или более переменных).
В зависимости от критерия оптимальности:
- однокритериальная (критерий оптимальности = 1),
- многокритериальная (критериев оптимальности > 1) .

Методы решения

Линейное и нелинейное программирование
Задача линейного программирования
(ограничения и целевая функция представляют собой линейные функции, то есть, многочлены первой степени)
Задача нелинейного программирования
(ограничения, либо целевая функция (либо и то, и другое) выражены в нелинейном виде)

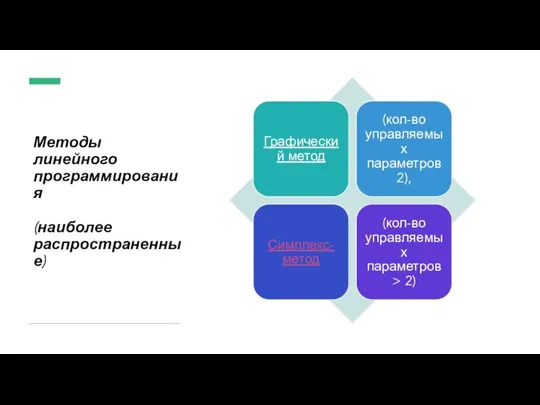
Методы линейного программирования
(наиболее распространенные)

Задача двухпараметрической оптимизации
Пример 1
Производственная задача
Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола - 20 единиц (футов красного дерева). Стул требует 10 человеко-часов, стол - 15. Имеется 400 единиц материала и 400 человеко-часов. Прибыль при производстве стула - 45 долларов США, при производстве стола - 80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?

Задача двухпараметрической оптимизации
Составим оптимизационную модель в общем виде:
Пусть управляемые параметры (параметры, значения которых требуется оптимизировать) это кол-во изготовленных стульев – Х1 и кол-во изготовленных столов – Х2.
Критерий оптимальности - прибыль, которая должна быть максимальной, тогда целевая функция будет выглядеть:
Есть ограничения по материалу и человеко-часам, которые можно представить в виде:
Однако, так как управляемые параметры натуральные числа, то они должны быть больше или равны 0.

Задача двухпараметрической оптимизации
Решим задачу графическим методом:
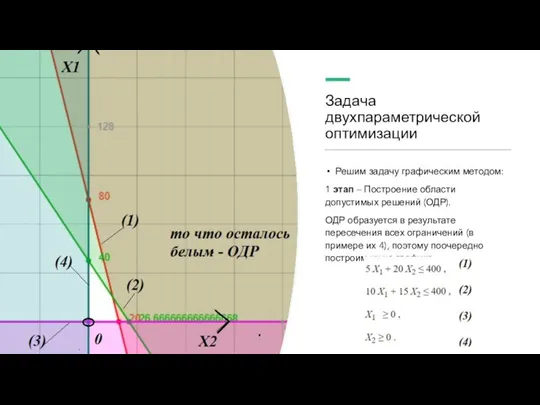
1 этап – Построение области допустимых решений (ОДР).
ОДР образуется в результате пересечения всех ограничений (в примере их 4), поэтому поочередно построим их на графике

Построение ограничений
ограничение – это уравнение прямой.
Найдем точки пересечения прямой с осями координат
Точка 1, если Х1=0, то Х2=400/20=20,
Точка 2, если Х2=0, то Х1=400/5=80,
НО прямая – это знак =, а у нас неравенство,
поэтому зону точек при которых неравенство не выполняется необходимо вычеркнуть из возможных вариантов ответа.
Аналогично, строятся остальные ограничения.

Задача двухпараметрической оптимизации
2 этап – построение линий уровня (линий постоянного значения функции)
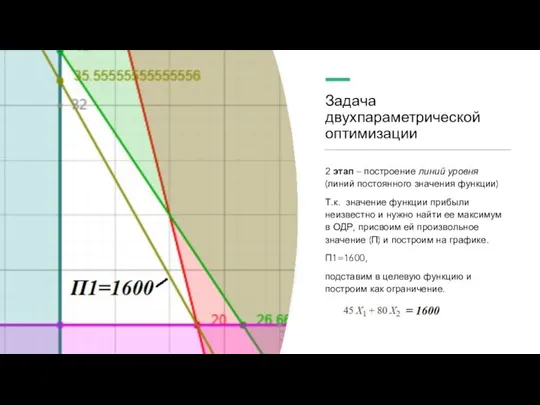
Т.к. значение функции прибыли неизвестно и нужно найти ее максимум в ОДР, присвоим ей произвольное значение (П) и построим на графике.
П1=1600,
подставим в целевую функцию и построим как ограничение.

Задача двухпараметрической оптимизации
Далее строим еще линию уровня c другим значением прибыли.
П2=800,
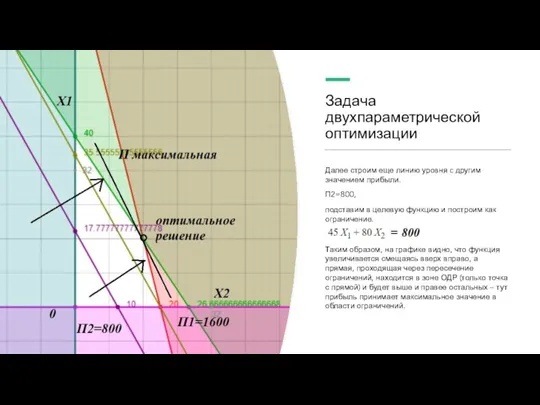
подставим в целевую функцию и построим как ограничение.
Таким образом, на графике видно, что функция увеличивается смещаясь вверх вправо, а прямая, проходящая через пересечение ограничений, находится в зоне ОДР (только точка с прямой) и будет выше и правее остальных – тут прибыль принимает максимальное значение в области ограничений.

Задача двухпараметрической оптимизации
Чтобы записать ответ, найдем координаты точки, опустив перпендикуляры к осям.
Получилось Х1 =16, Х2 =16.
Подставим в функцию прибыли
Пмакс=45∙16+80∙16=2000.
Ответ: в рамках ограничений по ресурсам и человеко-часам максимальная прибыль 2000 долларов США будет получена, если изготовить 16 стульев и 16 столов.