Функция у = kx², её график и свойства

Классная работа
20.01.2021
Функция у = kx²,
её график и свойства

Домашнее задание
§19 повторить;
§20 прочитать в учебнике;
Выполнить тест

Выполните: №19.11 (устно)
Задайте число k так, чтобы график функции y = kx² был расположен:
a) в первой и второй четвертях;
б) в третьей и четвертой четвертях.
a) График функции расположен в верхней полуплоскости, значит k > 0.
б) График функции расположен в нижней полуплоскости, значит k < 0.

№19.16 (б, г)
Принадлежит ли графику функции y = – 220x² точка:
б) В (4; –880)
y = – 220x²
– 880 = – 220 ∙ 4²
– 880 = – 220 ∙ 16
– 880 = – 3520
т. В не принадлежит графику функции
в) D (1,5; –495)
– 495 = – 220 ∙ 1,5²
– 495 = – 220 ∙ 2,25
– 495 = – 495
т. D принадлежит графику функции

№19.17 (г)
Найдите коэффициент k в уравнении параболы y = kx², зная, что парабола проходит через точку:
б) L (4; –96)
– 96 = k ∙ 4²
Ответ:
– 96 = k ∙ 16

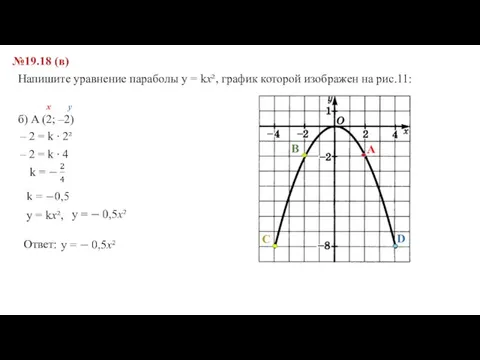
№19.18 (в)
Напишите уравнение параболы y = kx², график которой изображен на рис.11:
б) A (2; –2)
– 2 = k ∙ 2²
Ответ:
– 2 = k ∙ 4
A
В
С
D
y = kx²,

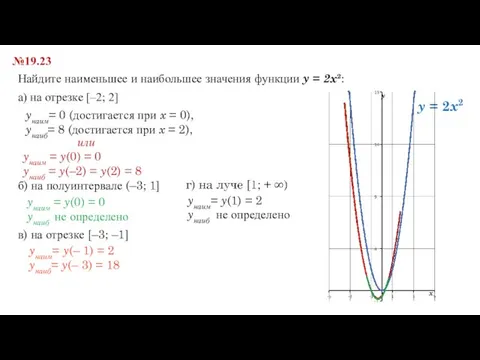
№19.23
Найдите наименьшее и наибольшее значения функции y = 2x²:
а) на отрезке [–2; 2]
yнаим= 0 (достигается при x = 0),
yнаиб= 8 (достигается при x = 2),
или
yнаим = y(0) = 0
yнаиб = y(–2) = y(2) = 8
б) на полуинтервале (–3; 1]
yнаим = y(0) = 0
yнаиб не определено
в) на отрезке [–3; –1]
yнаим= y(– 1) = 2
yнаиб= y(– 3) = 18
yнаим= y(1) = 2
yнаиб не определено

№19.26 (в)
Найдите точки пересечения графиков функций:
в) y = – 3x² и y = – 3x
Аналитический способ (без построения):
Ответ:
y = – 3x² и y = – 3x
– 3x² = – 3x
– 3x² + 3x = 0
– 3x ( x – 1) = 0
– 3x = 0 или x – 1 = 0
x = 0 или x = 1
Если x = 1, то y = – 3 ∙ 1 = – 3
Если x = 0, то y = – 3 ∙ 0 = 0
(x; y) – точка пересечения
(x; y) – точка пересечения
(0; 0), (1; – 3) – точки пересечения
Если x = 1, то y = – 3 ∙ 1 = – 3
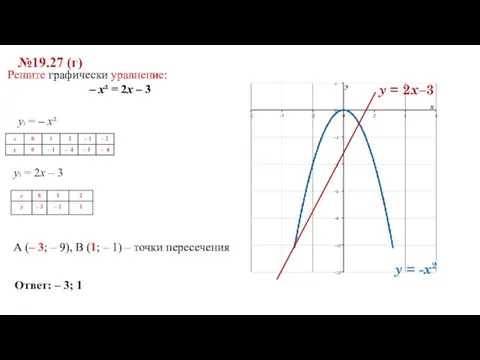
Если x = 0, то y = – 3 ∙ 0 = 0

№19.27 (г)
Решите графически уравнение:
– x² = 2x – 3
y1 = – x²
y2 = 2x – 3
Ответ: – 3; 1
А (– 3; – 9), В (1; – 1) – точки пересечения
А (– 3; – 9), В (1; – 1) – точки пересечения
Решите графически уравнение:
– x² = 2x – 3
y = -x2
y
x
y = 2x–3