Содержание
- 2. «1» Все показатели, с помощью которых мы характеризуем явления общественной жизни, взаимосвязаны между собой. Например: Валовый
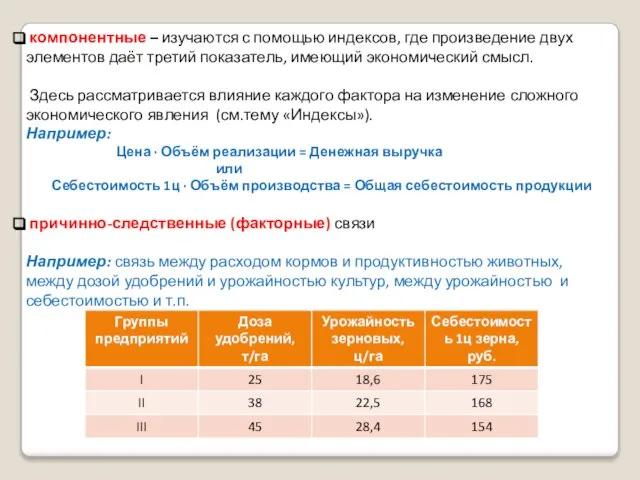
- 3. компонентные – изучаются с помощью индексов, где произведение двух элементов даёт третий показатель, имеющий экономический смысл.
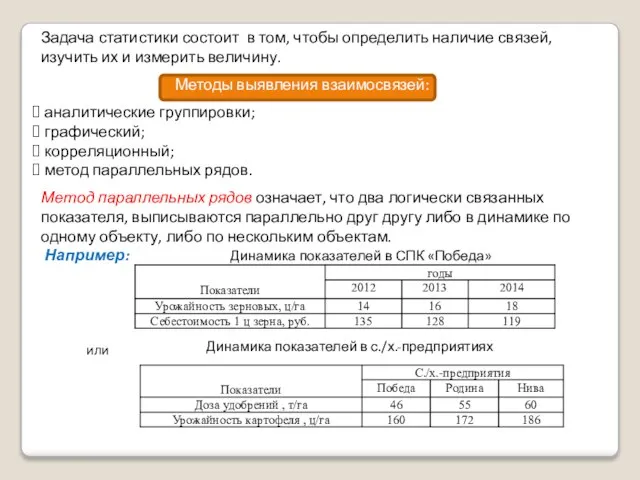
- 4. Задача статистики состоит в том, чтобы определить наличие связей, изучить их и измерить величину. Методы выявления
- 5. «2» Различают два вида зависимости между экономическими явлениями: функциональную и корреляционную. Зависимость между двумя величинами Х
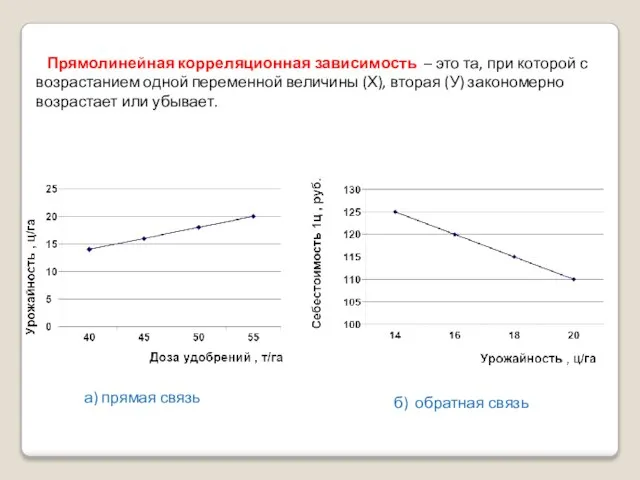
- 6. Прямолинейная корреляционная зависимость – это та, при которой с возрастанием одной переменной величины (Х), вторая (У)
- 7. Корреляционная связь описывается математическими уравнениями. Корреляционное уравнение прямой линии имеет вид: у = а + вх,
- 8. Данные итоговой строки таблицы подставляются в систему уравнений для решения. В результате получаем уравнение количественной связи
- 9. Для характеристики степени тесноты связи используются: коэффициент корреляции (r) коэффициент детерминации (D) __ _ _ х∙у
- 10. Коэффициент корреляции изменяется в пределах от – 0,999 до + 0,999 , но не может быть
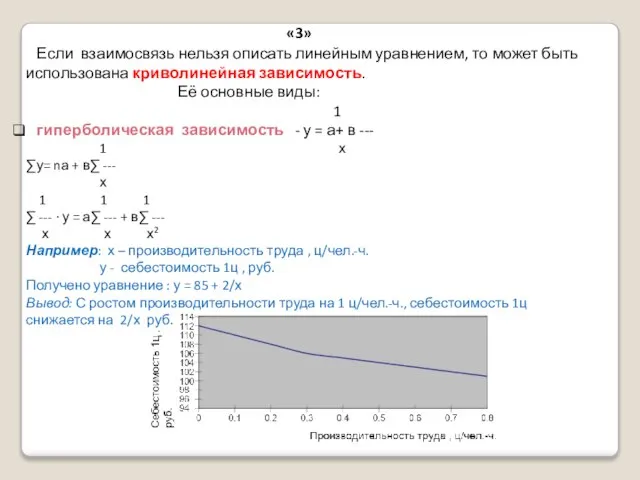
- 11. Вывод: С ростом производительности труда на 1 ц/чел.-ч., себестоимость 1ц снижается на 2/х руб. «3» Если
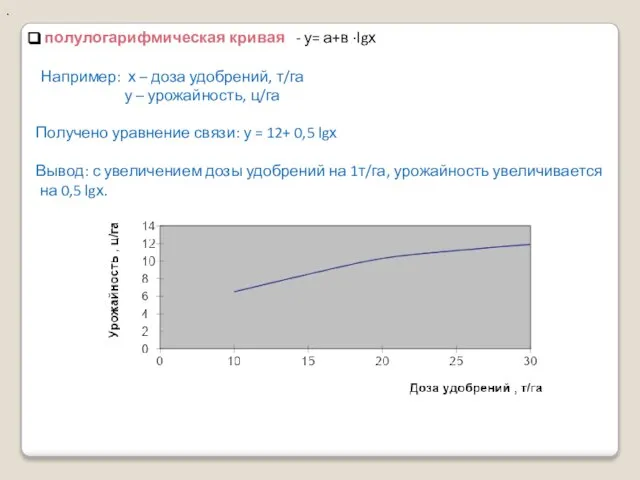
- 12. . полулогарифмическая кривая - у= а+в ·lgх Например: х – доза удобрений, т/га у – урожайность,
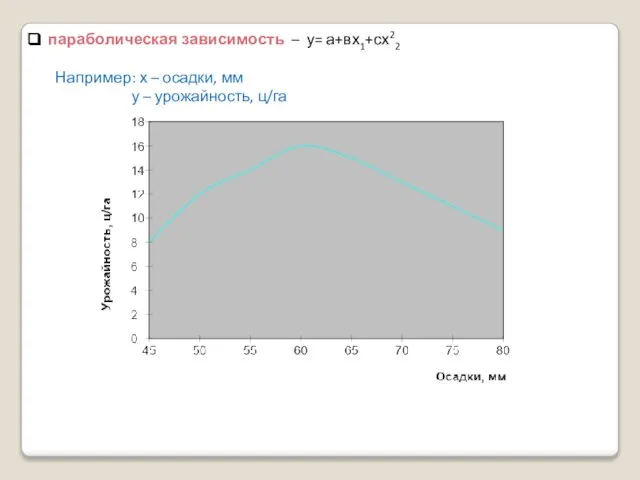
- 13. параболическая зависимость – у= а+вх1+сх22 Например: х – осадки, мм у – урожайность, ц/га
- 15. Скачать презентацию






 Прямоугольный треугольник
Прямоугольный треугольник Решение простейших тригонометрических уравнений sin х = а, cos х = а
Решение простейших тригонометрических уравнений sin х = а, cos х = а Измерение углов транспортиром. 5 класс
Измерение углов транспортиром. 5 класс Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Устная нумерация чисел от 1 до 20
Устная нумерация чисел от 1 до 20 Нестандартный урок математики. Проведен учителем I категории Крутько В.И.
Нестандартный урок математики. Проведен учителем I категории Крутько В.И. Сложение чисел с разными знаками
Сложение чисел с разными знаками Уравнения высших степеней
Уравнения высших степеней Великолепная алгебра и занимательная геометрия
Великолепная алгебра и занимательная геометрия Урок математики. Замени произведение суммой
Урок математики. Замени произведение суммой Строение функции, свойства, графики
Строение функции, свойства, графики Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM Односторонние пределы
Односторонние пределы Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Треугольная пирамида
Треугольная пирамида Сколько? Как? Почему? Математическая игра
Сколько? Как? Почему? Математическая игра Презентация на тему Сфера и шар (11 класс)
Презентация на тему Сфера и шар (11 класс)  Призма и пирамида
Призма и пирамида Прямоугольный треугольник. Тренажер. 8 класс
Прямоугольный треугольник. Тренажер. 8 класс Лінійне рівнянь з однією змінною. 7 клас
Лінійне рівнянь з однією змінною. 7 клас Решение тригонометрических уравнений
Решение тригонометрических уравнений Определенный интеграл
Определенный интеграл Числовые и буквенные выражения. Классная работа
Числовые и буквенные выражения. Классная работа Логические и традиционные головоломки
Логические и традиционные головоломки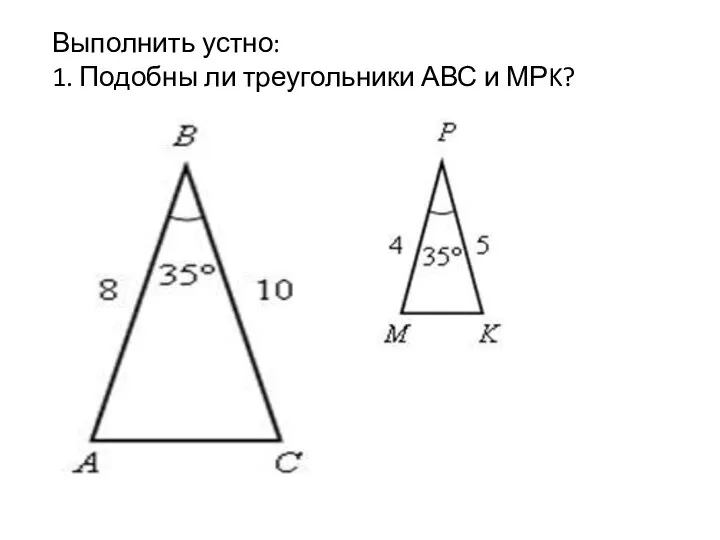 Признаки подобия треугольников. Урок 34
Признаки подобия треугольников. Урок 34 философия стоицизма в древнем риме
философия стоицизма в древнем риме Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)  Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение
Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение