Содержание
- 2. Определение производной функции? Производной функции в данной точке называется предел отношения приращения функции в этой точке
- 3. Устная работа 1 сosх sinх+12
- 4. Устная работа
- 5. Используя определение производной функции, решают ряд задач в алгебре, физике, химии. Рассмотрим физический смысл производной. материальная
- 6. Задача: Точка движется прямолинейно по закону s(t) = t3+ 2t ( где s(t) – измеряется в
- 7. Что мы сделали за часть урока? Повторили определение производной функции и формулы дифференцирования. Решили задачу на
- 8. Задача: По прямой движется материальная точка, скорость которой в момент времени t задается формулой v(t) =
- 9. При решении задачи, мы, зная производную функции, восстановили ее первичный образ. Эта операция восстановления - операция
- 10. y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈
- 11. Операция дифферен-цирования функция y = F(х) (первообразная) y = f(х) производная Операция интегри- рования В математике
- 12. Запомните: Первообразная – это родитель производной:
- 13. Задача: Найдите все первообразные для функций: f(х)=3 f(х)= х2 f(х)=cosx f(х)=12 f(х)=х5
- 14. Три правила нахождения первообразных Если функции у=f(x) и у=g(x) имеют на промежутке первообразные соответственно у=F(x) и
- 16. Самостоятельно Для функции y=f(x) найдите хотя бы одну первообразную:
- 17. Первообразная С какой новой операцией вы познакомились? Подведем итоги урока. Нахождение первообразной функции. Как называется процесс
- 19. Скачать презентацию
















 деление многочлена на многочлен столбиком
деление многочлена на многочлен столбиком Логарифмические уравнения
Логарифмические уравнения Основы функционального анализа
Основы функционального анализа Diskretnaya_matematika_sootvetstvia
Diskretnaya_matematika_sootvetstvia Математика на страже здоровья
Математика на страже здоровья Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Понятие логарифма
Понятие логарифма Компьютерное решение задач по теме Арифметическая прогрессия
Компьютерное решение задач по теме Арифметическая прогрессия Математические паззлы Домино. Математика 1 класс
Математические паззлы Домино. Математика 1 класс Алгебра логики
Алгебра логики Решение практических задач с применением среднего арифметического. 5 класс
Решение практических задач с применением среднего арифметического. 5 класс Математика на каждый день
Математика на каждый день Презентация на тему Решение планиметрических задач на нахождение площади фигуры
Презентация на тему Решение планиметрических задач на нахождение площади фигуры  Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций Бинарные отношения
Бинарные отношения Деление двузначного числа на однозначное
Деление двузначного числа на однозначное Координатные векторы
Координатные векторы Функции многих переменных: определение, предел, непрерывность, частные производные. Лекция 1
Функции многих переменных: определение, предел, непрерывность, частные производные. Лекция 1 Линейная алгебра
Линейная алгебра Векторы. Тест
Векторы. Тест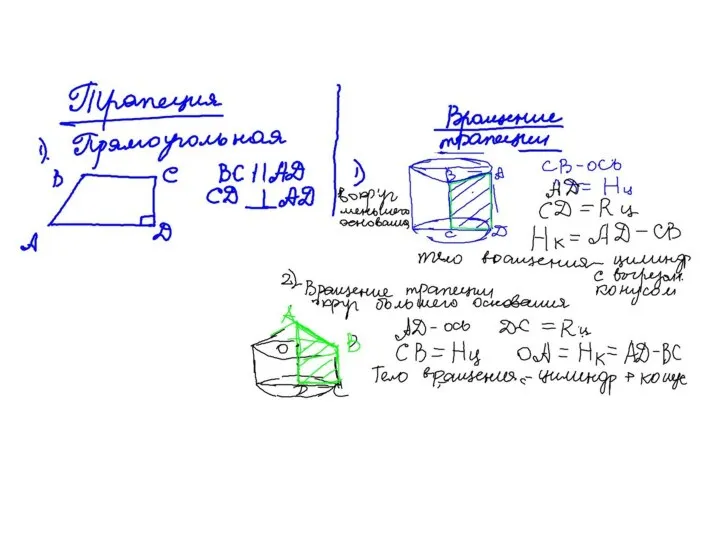 Вращение трапеции
Вращение трапеции Признаки равенства треугольников
Признаки равенства треугольников Что такое параметр? Тема 1
Что такое параметр? Тема 1 Параллельность прямых
Параллельность прямых Численные решения обыкновенных дифференциальных уравнений (ОДУ)
Численные решения обыкновенных дифференциальных уравнений (ОДУ) Способы решения показательных уравнений
Способы решения показательных уравнений Жили-были числа
Жили-были числа Поможем Буратино! Цель: формировать мыслительные операции
Поможем Буратино! Цель: формировать мыслительные операции