достаточной полнотой закладывают понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучше.
Решая задачи указанного типа, наблюдаем, с одной стороны, абстрактный характер математических понятий, а с другой большую эффективную их применимость к решению жизненных практических задач.
Выполняя данную работу, я глубже изучила возможности программы «Живая математика», научилась выполнять динамические чертежи, имитируя построение циркулем и линейкой, проводить вычисления и, наконец создавать презентации в этой программе.



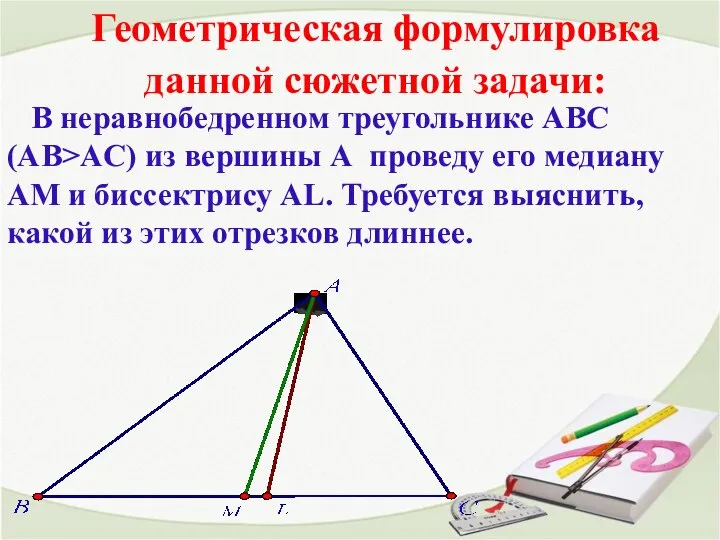



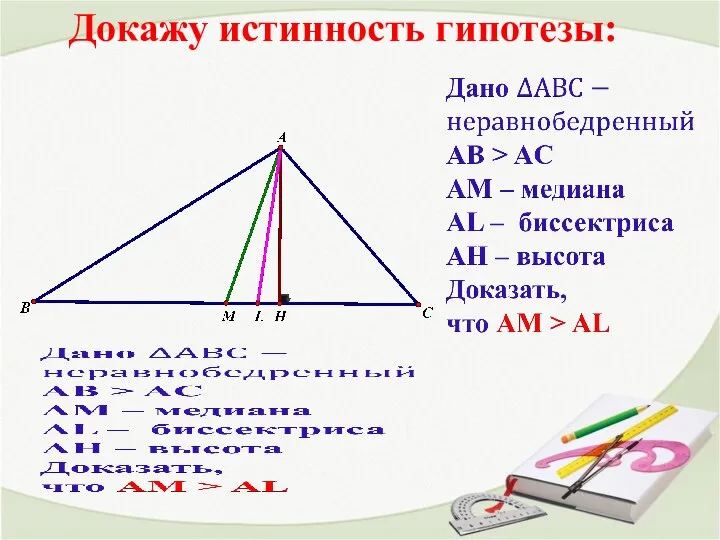
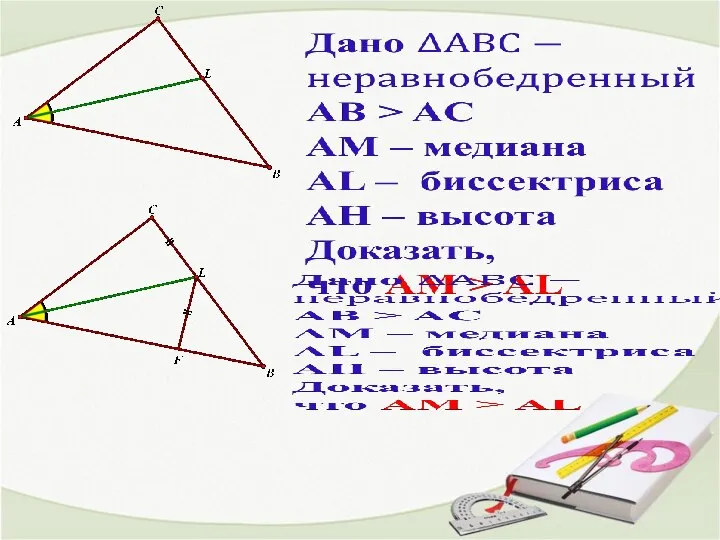
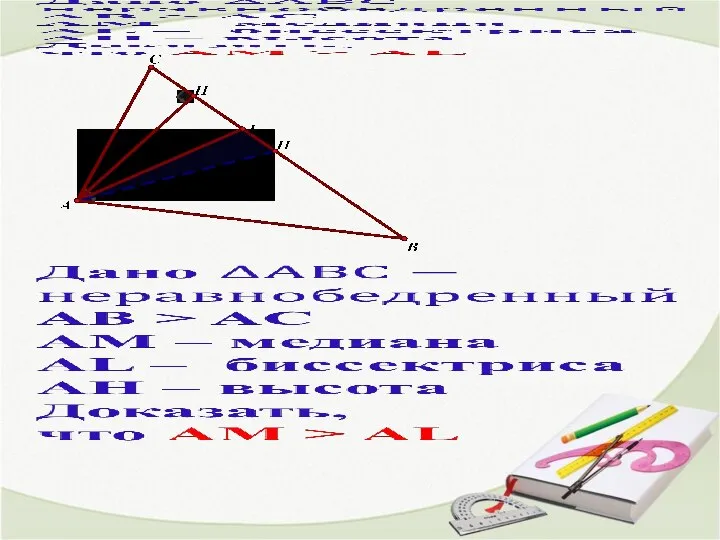

 Геометрические построения
Геометрические построения Найдите площадь ABCD
Найдите площадь ABCD Презентация на тему Движение фигур в стереометрии
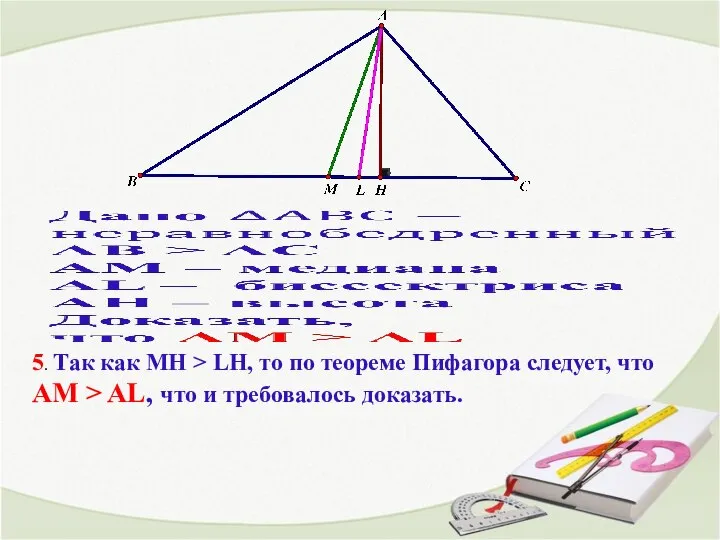
Презентация на тему Движение фигур в стереометрии  Решение задач. Пирамида
Решение задач. Пирамида Презентация на тему Анализ геометрической формы предмета
Презентация на тему Анализ геометрической формы предмета  Презентация на тему Решение планиметрических задач на нахождение геометрических величин
Презентация на тему Решение планиметрических задач на нахождение геометрических величин  Параллельность прямых
Параллельность прямых Презентация на тему Число и цифра 2 (1 класс)
Презентация на тему Число и цифра 2 (1 класс)  Линейное пространство. N-мерные векторы и действия над ними. Тема 1
Линейное пространство. N-мерные векторы и действия над ними. Тема 1 Конструктивная геометрия
Конструктивная геометрия Дифференциальные уравнения
Дифференциальные уравнения Основное логарифмическое тождество
Основное логарифмическое тождество Второй признак равенства треугольников. Теорема
Второй признак равенства треугольников. Теорема Интересные факты про математику
Интересные факты про математику Преобразование буквенных выражений. Правила математического синтаксиса
Преобразование буквенных выражений. Правила математического синтаксиса Порядок действий в выражениях со скобками
Порядок действий в выражениях со скобками Парный регрессионный анализ
Парный регрессионный анализ Многогранник и тела вращения. Тетраэдр, пирамида, цилиндр, конус, сфера и шар
Многогранник и тела вращения. Тетраэдр, пирамида, цилиндр, конус, сфера и шар Многоугольники
Многоугольники Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Основные правила построения сечений
Основные правила построения сечений Координаты вектора. Простейшие задачи в координатах
Координаты вектора. Простейшие задачи в координатах Операции над множествами
Операции над множествами Прямоугольный треугольник
Прямоугольный треугольник Задачи на проценты
Задачи на проценты ЕГЭ Профиль. Решение задания №11
ЕГЭ Профиль. Решение задания №11 Построение графиков функций
Построение графиков функций Аналитическая геометрия
Аналитическая геометрия