Содержание
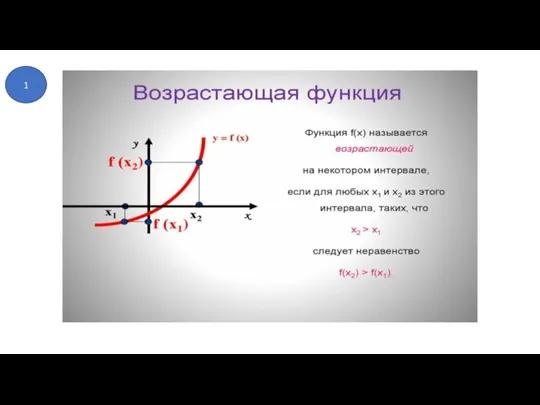
- 2. 1
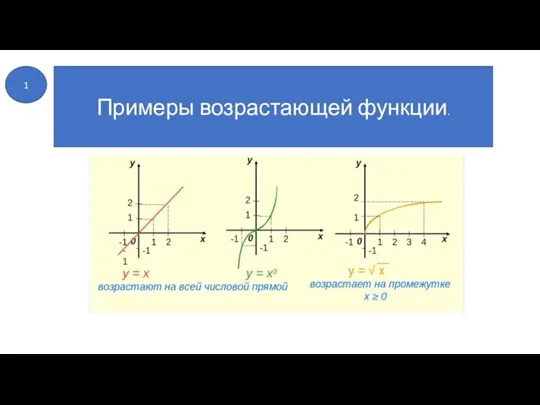
- 3. Примеры возрастающей функции. 1
- 4. 1
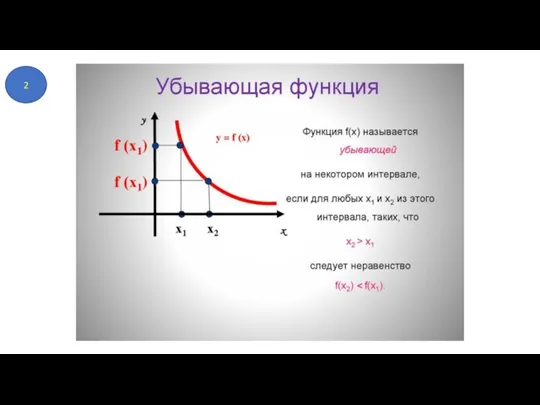
- 5. 2
- 6. Примеры возрастающей функции. 2
- 7. 2
- 8. 3
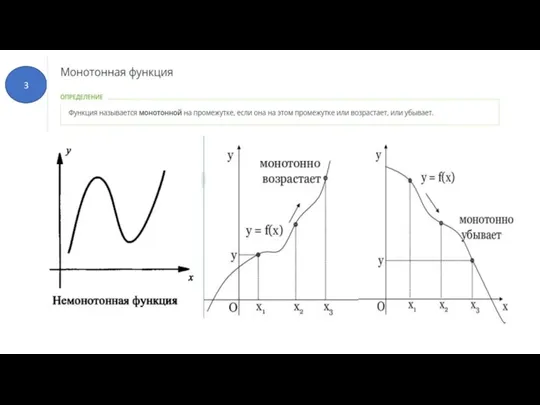
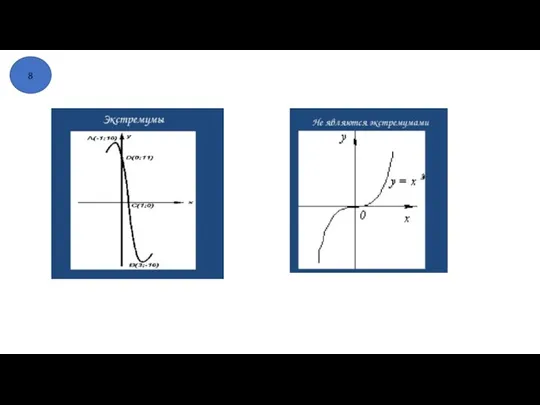
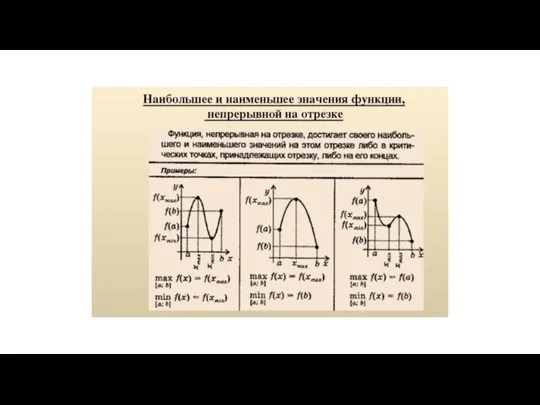
- 9. 3 Функция монотонно возрастает на промежутке [0; +∞) и монотонно убывает на промежутке (- ∞; 0]
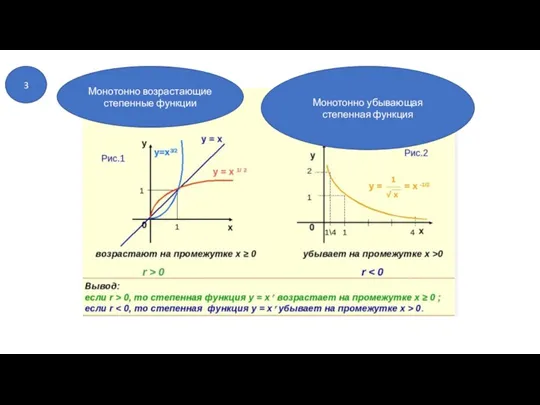
- 10. 3 Монотонно возрастающие степенные функции Монотонно убывающая степенная функция
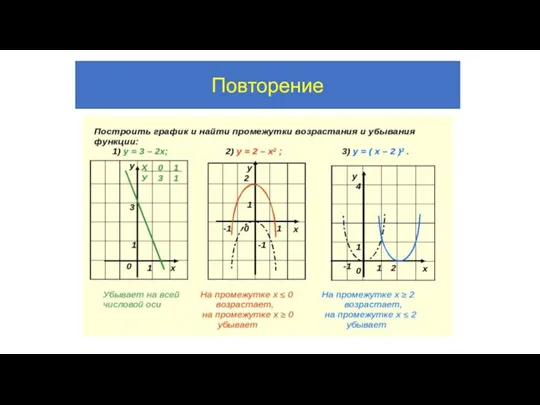
- 11. Повторение
- 12. Повторение
- 13. 4
- 14. 4
- 15. Алгоритм нахождения промежутков монотонности функции. 4
- 16. 4
- 17. Повторение
- 18. Повторение
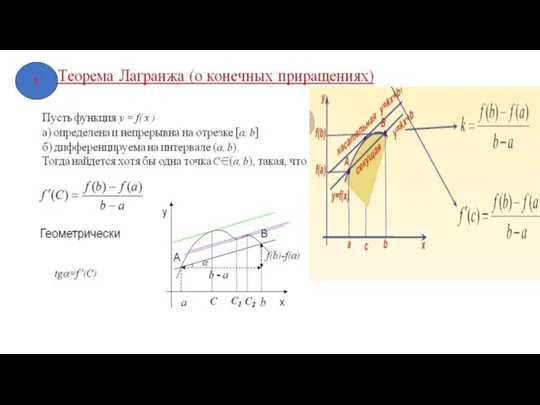
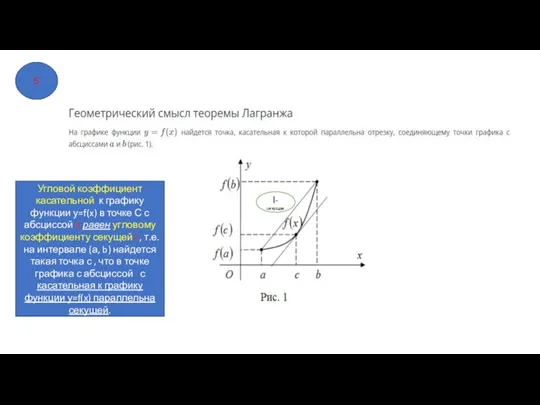
- 20. Угловой коэффициент касательной к графику функции у=f(x) в точке С с абсциссой с равен угловому коэффициенту
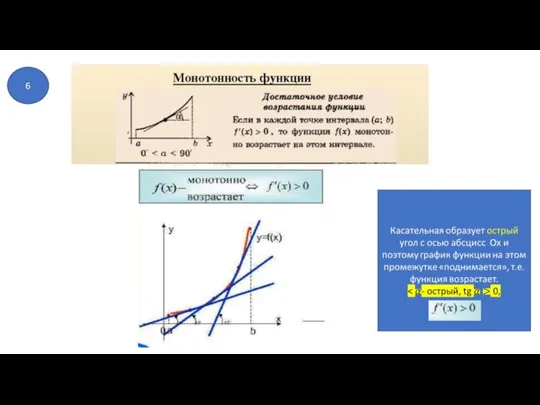
- 23. 6
- 24. 6
- 25. 6
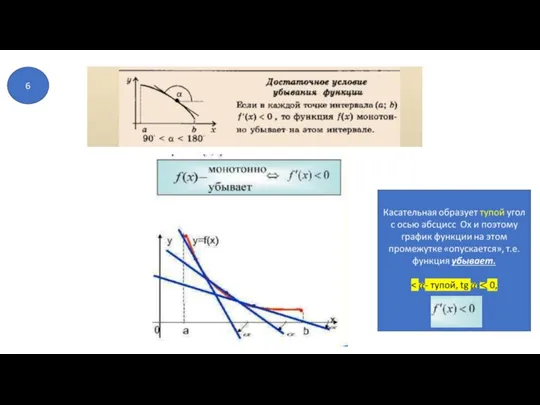
- 26. 7
- 27. Обобщение
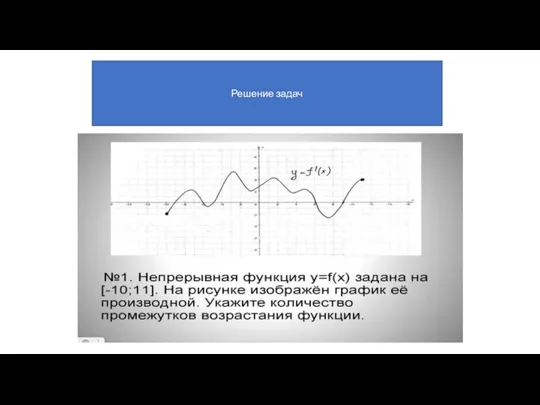
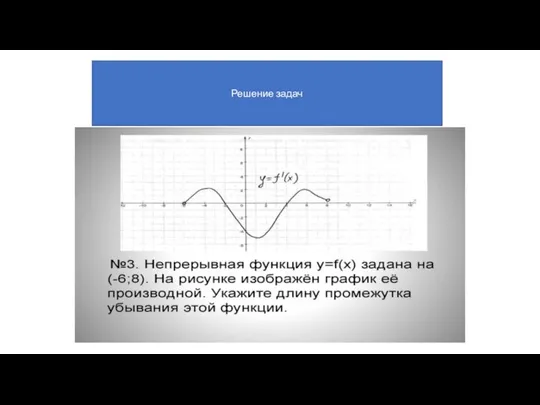
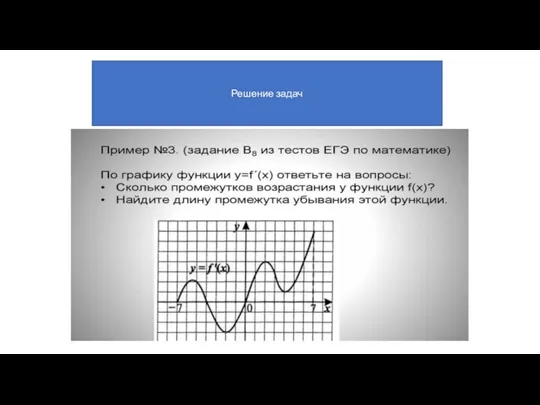
- 28. Решение задач
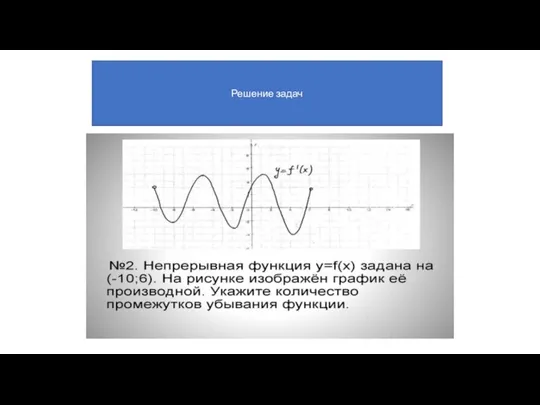
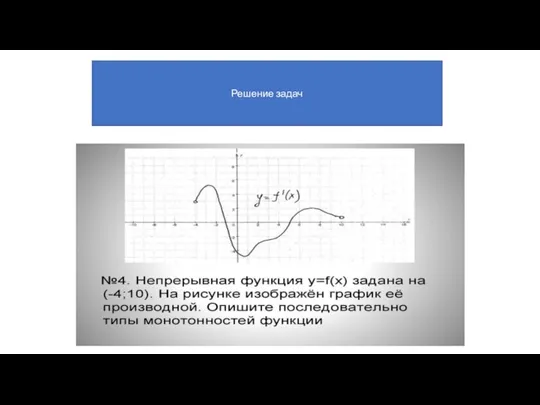
- 29. Решение задач
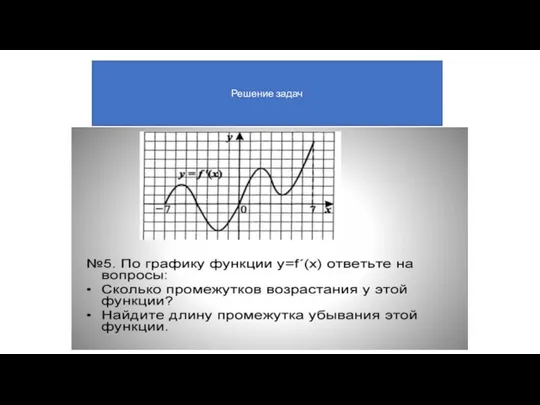
- 30. Решение задач
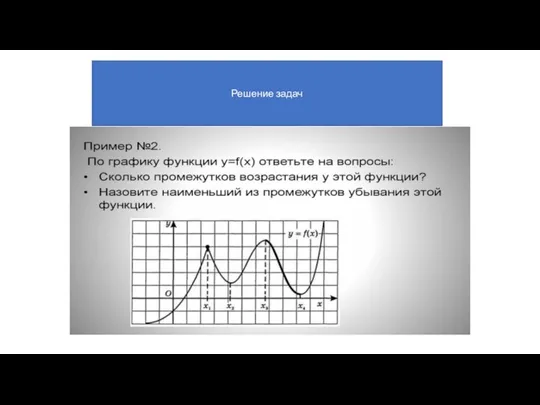
- 31. Решение задач
- 32. Решение задач
- 33. Решение задач
- 34. Решение задач
- 35. 8
- 36. 8
- 37. 8
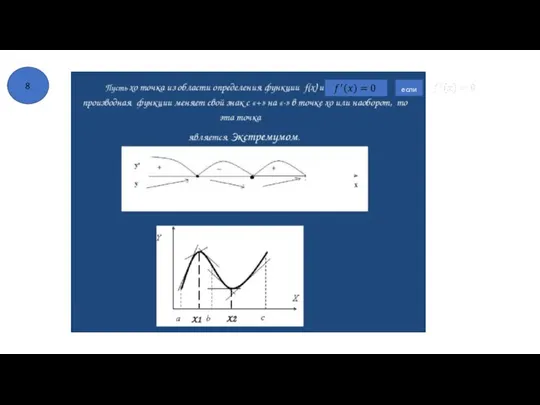
- 38. если 8
- 39. 8
- 40. 8
- 41. 8
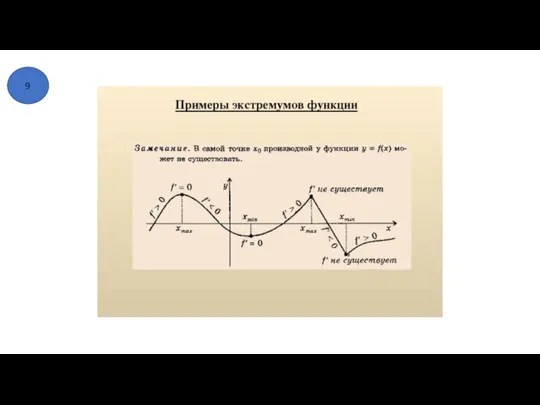
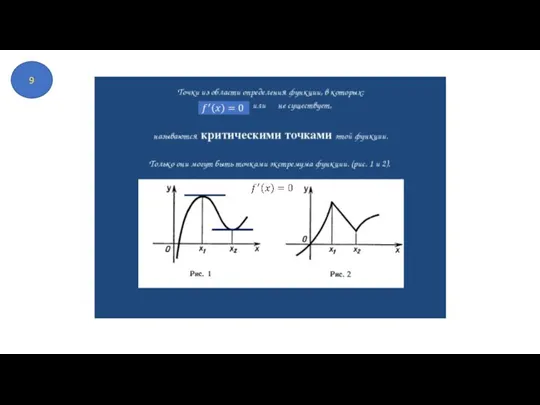
- 42. 9
- 43. 9
- 44. 9
- 45. 9
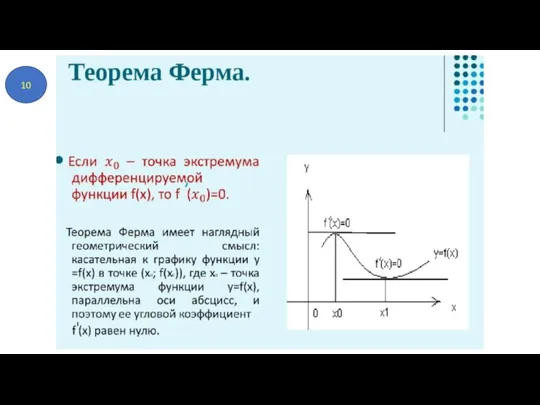
- 47. 11
- 48. 10
- 59. Скачать презентацию



![3 Функция монотонно возрастает на промежутке [0; +∞) и монотонно убывает на промежутке (- ∞; 0]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1018979/slide-8.jpg)















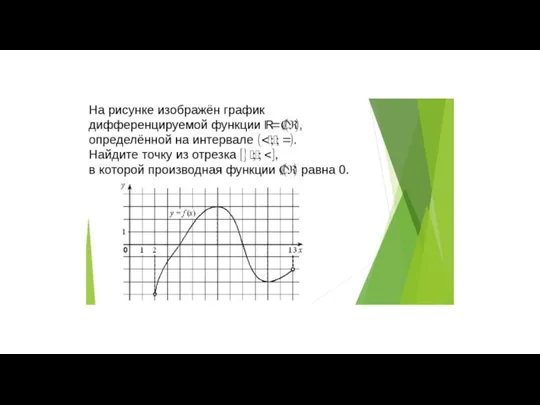
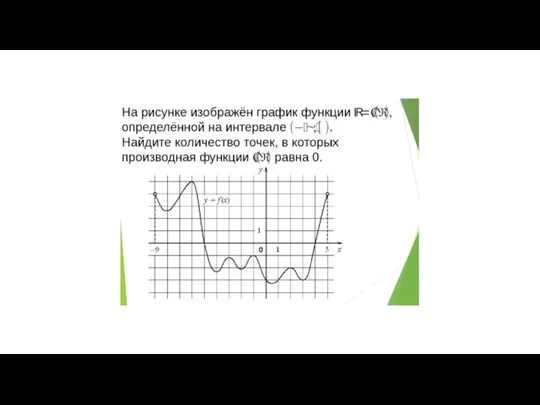
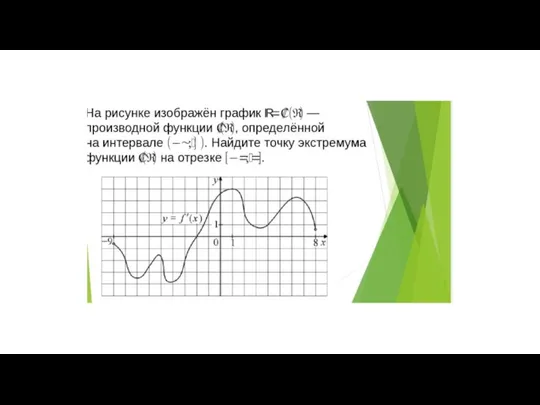
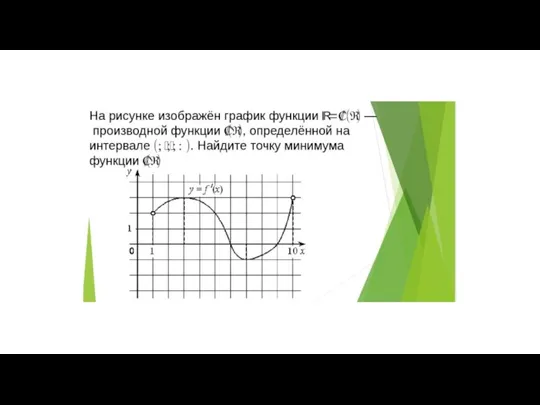
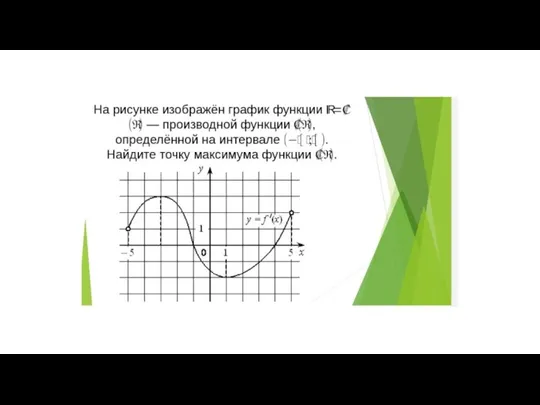
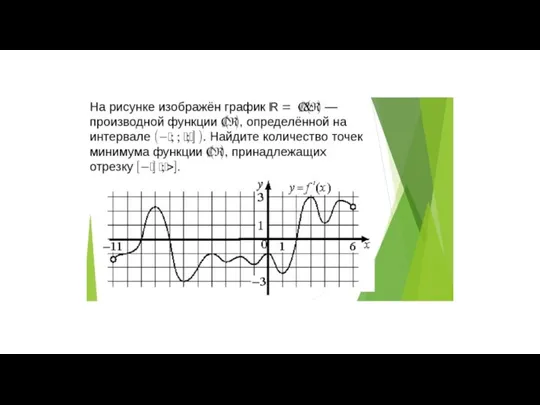
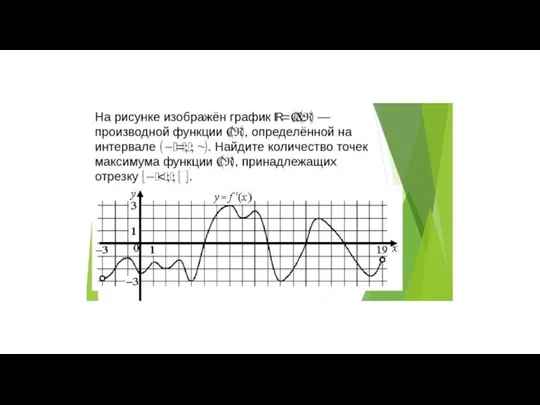
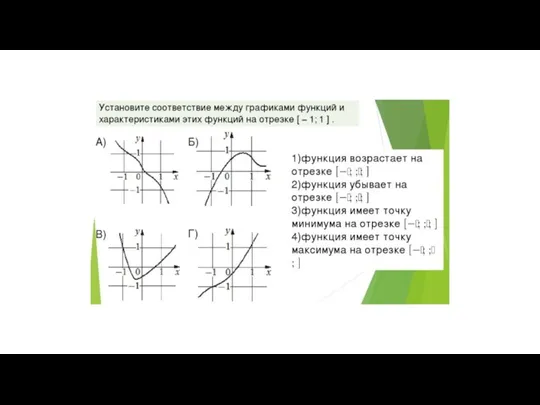
 Типы моделей процессов и систем
Типы моделей процессов и систем Осевая и центральная симметрии
Осевая и центральная симметрии Математика для родителей
Математика для родителей Нумерология. Пифагор
Нумерология. Пифагор Архитектура и параллелепипед
Архитектура и параллелепипед Известное и неизвестное
Известное и неизвестное Простейшие преобразования графиков
Простейшие преобразования графиков Викторина по математике: Где логика?
Викторина по математике: Где логика? Медианы, биссектрисы и высоты треугольника. Урок геометрии в 7 классе
Медианы, биссектрисы и высоты треугольника. Урок геометрии в 7 классе Геометрия (8 класс)
Геометрия (8 класс) Площадь параллелограмма
Площадь параллелограмма Прямая на плоскости
Прямая на плоскости Обработка данных. Задача о наилучшем среднеквадратическом приближении (задача о тренде)
Обработка данных. Задача о наилучшем среднеквадратическом приближении (задача о тренде) Числовые и буквенные выражения. (5 класс)
Числовые и буквенные выражения. (5 класс) Решение треугольников
Решение треугольников Знаете ли вы... Высота, длина, вес
Знаете ли вы... Высота, длина, вес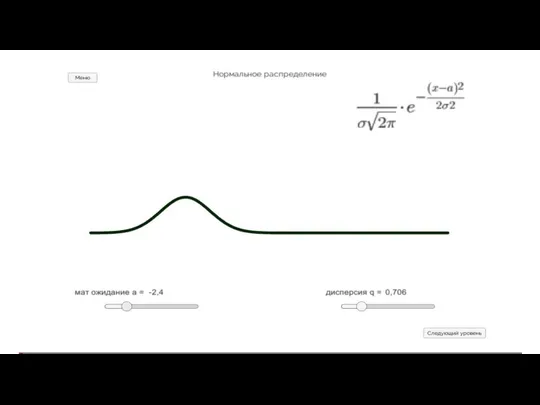 Критерий Пирсона
Критерий Пирсона Олимпийские игры: история, современность и математика
Олимпийские игры: история, современность и математика Поворот. 9 класс
Поворот. 9 класс Число π. Длина окружности
Число π. Длина окружности Производная. Сумма бесконечной геометрической прогрессии
Производная. Сумма бесконечной геометрической прогрессии Сфера и шар
Сфера и шар Porządki kompozycji symetria i asymetria
Porządki kompozycji symetria i asymetria Тема: 14 -
Тема: 14 - Решение составных задач
Решение составных задач Презентация на тему Квадратичная функция и ее график (8 класс)
Презентация на тему Квадратичная функция и ее график (8 класс)  Презентация на тему ТАБЛИЦА УМНОЖЕНИЯ
Презентация на тему ТАБЛИЦА УМНОЖЕНИЯ  Действия с дробями
Действия с дробями