Содержание
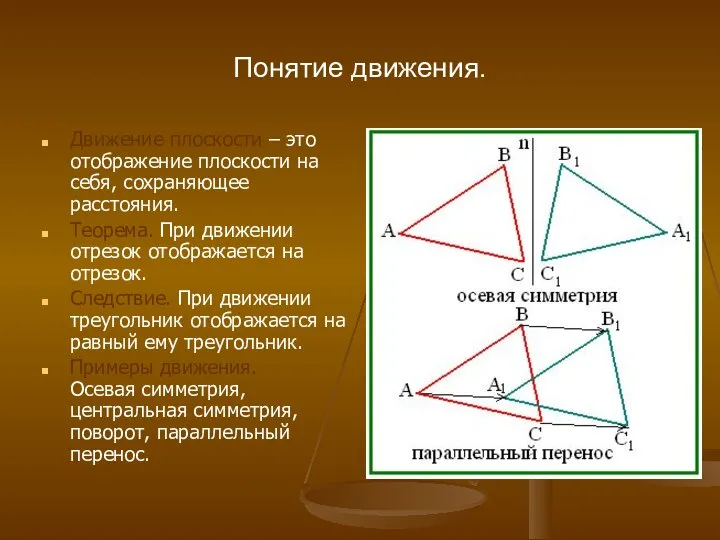
- 2. Понятие движения. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния. Теорема. При движении отрезок
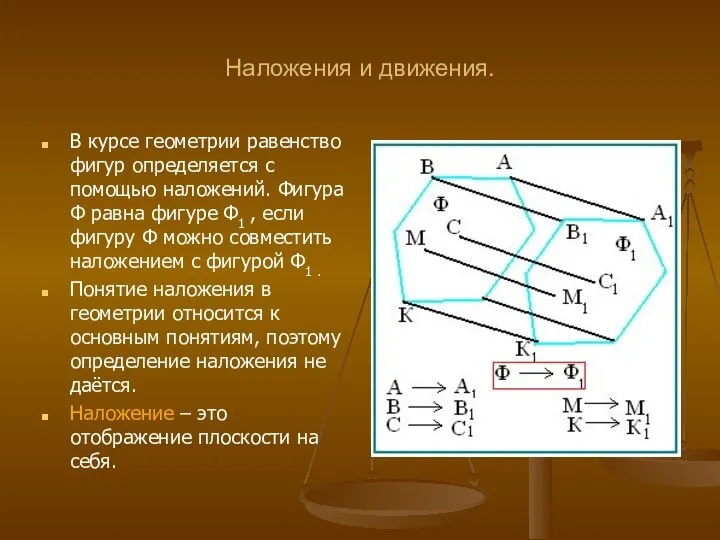
- 3. Наложения и движения. В курсе геометрии равенство фигур определяется с помощью наложений. Фигура Ф равна фигуре
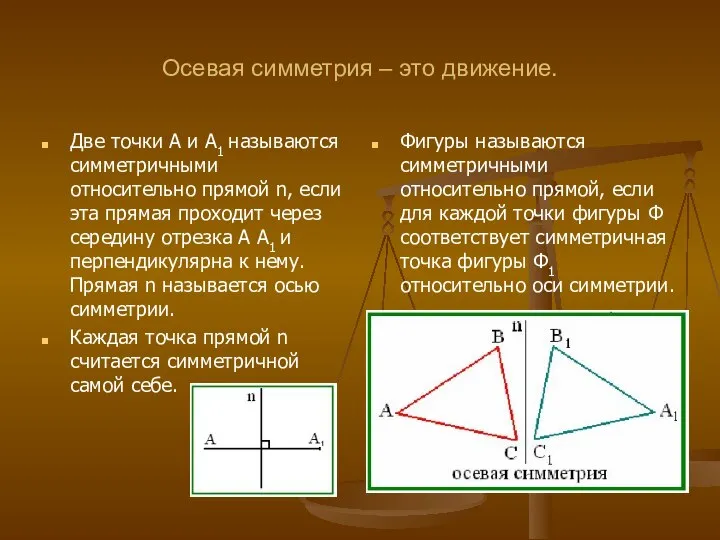
- 4. Осевая симметрия – это движение. Две точки А и А1 называются симметричными относительно прямой n, если
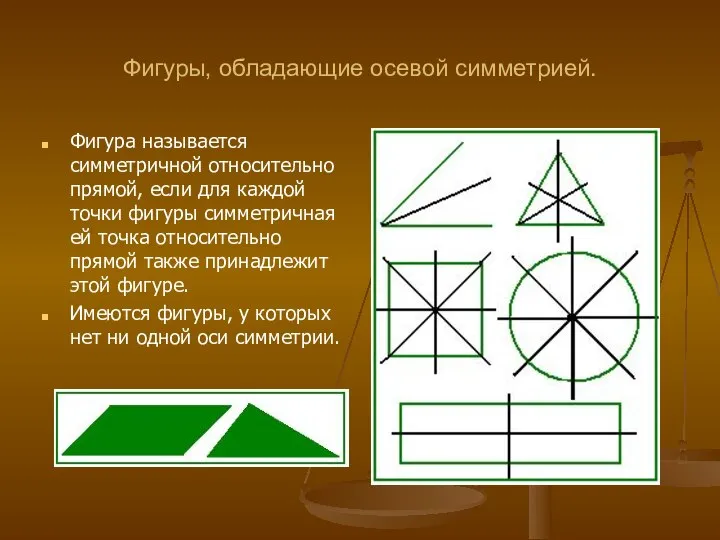
- 5. Фигуры, обладающие осевой симметрией. Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная ей
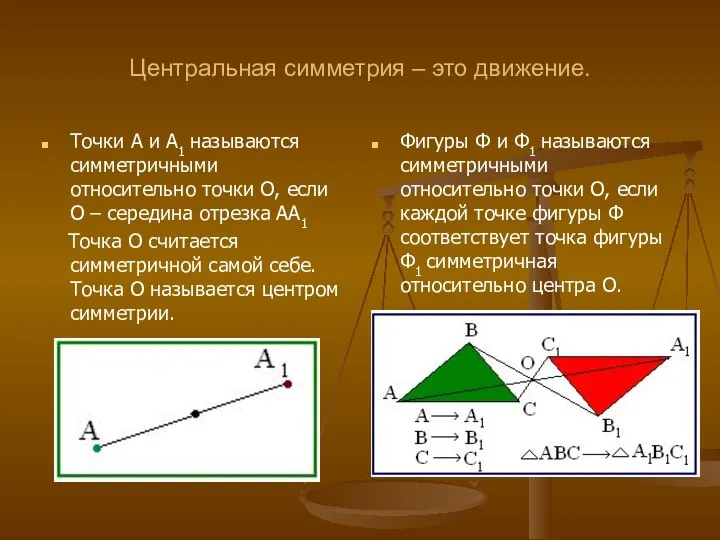
- 6. Центральная симметрия – это движение. Точки А и А1 называются симметричными относительно точки О, если О
- 7. Фигуры, обладающие центральной симметрией. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная
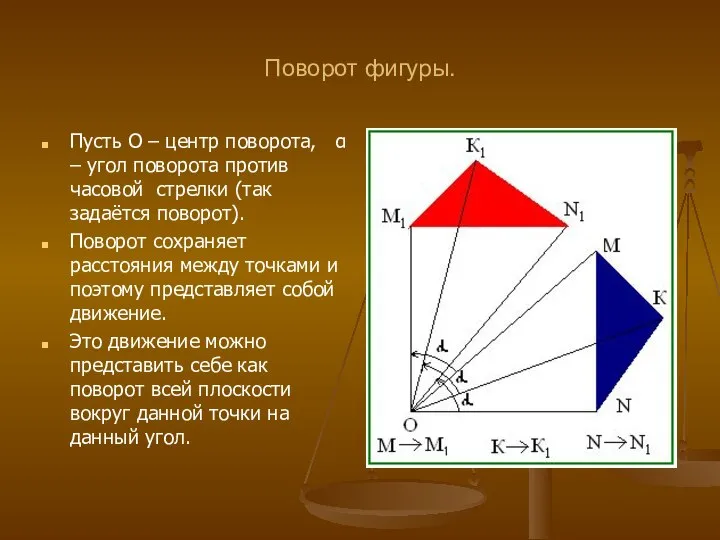
- 8. Поворот – это движение. Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на
- 9. Поворот фигуры. Пусть О – центр поворота, α – угол поворота против часовой стрелки (так задаётся
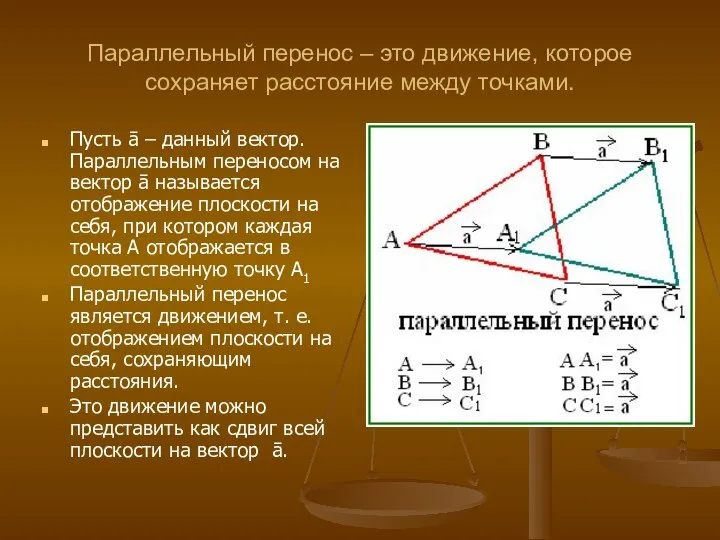
- 10. Параллельный перенос – это движение, которое сохраняет расстояние между точками. Пусть ā – данный вектор. Параллельным
- 11. Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья
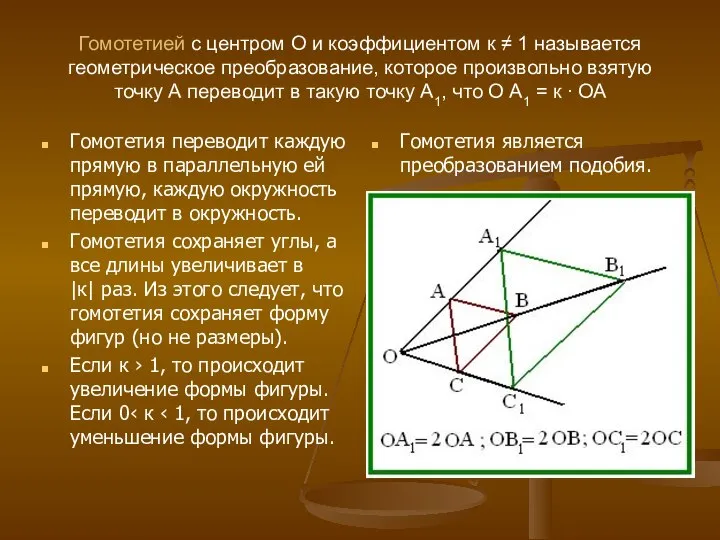
- 13. Гомотетией с центром О и коэффициентом к ≠ 1 называется геометрическое преобразование, которое произвольно взятую точку
- 14. Преобразование плоскости называется аффинным, если оно каждую прямую переводит в прямую, а параллельные между собой прямые
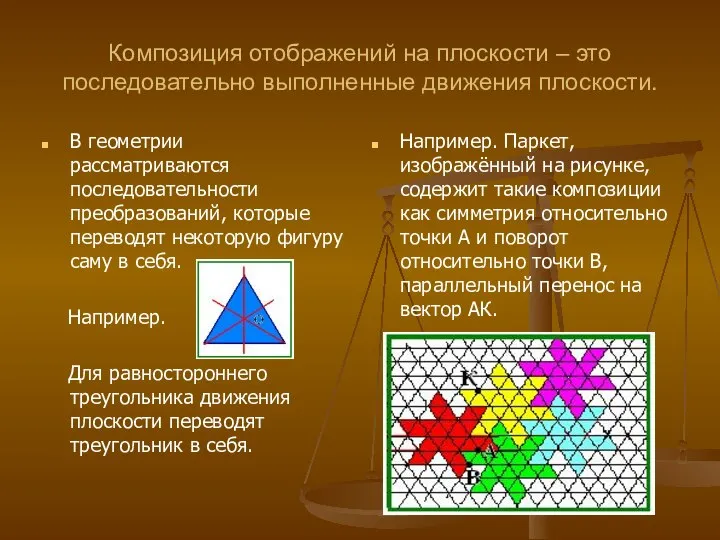
- 15. Композиция отображений на плоскости – это последовательно выполненные движения плоскости. В геометрии рассматриваются последовательности преобразований, которые
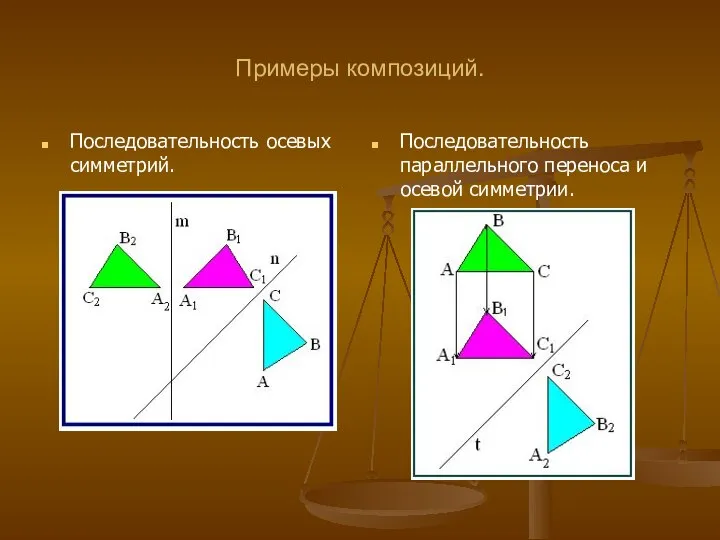
- 16. Примеры композиций. Последовательность осевых симметрий. Последовательность параллельного переноса и осевой симметрии.
- 18. Скачать презентацию





 Средние величины. (Лекция 4.2)
Средние величины. (Лекция 4.2) Элементы математической логики
Элементы математической логики Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Таблицы, часть 2, 9-11 классы
Таблицы, часть 2, 9-11 классы Цилиндр. Цилиндр в архитектуре города Хабаровска
Цилиндр. Цилиндр в архитектуре города Хабаровска Площадь четырёхугольника
Площадь четырёхугольника Интерактивная игра Состав числа в пределах первого десятка
Интерактивная игра Состав числа в пределах первого десятка Простейшие преобразования графиков
Простейшие преобразования графиков Деление одночлена на одночлен
Деление одночлена на одночлен Формула Стирлинга
Формула Стирлинга Запись многозначных чисел
Запись многозначных чисел Функции и предупреждающие знаки дорожного движения. 11 класс
Функции и предупреждающие знаки дорожного движения. 11 класс Многогранники. Виды многогранников
Многогранники. Виды многогранников Логика. Введение
Логика. Введение Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Производная функции
Производная функции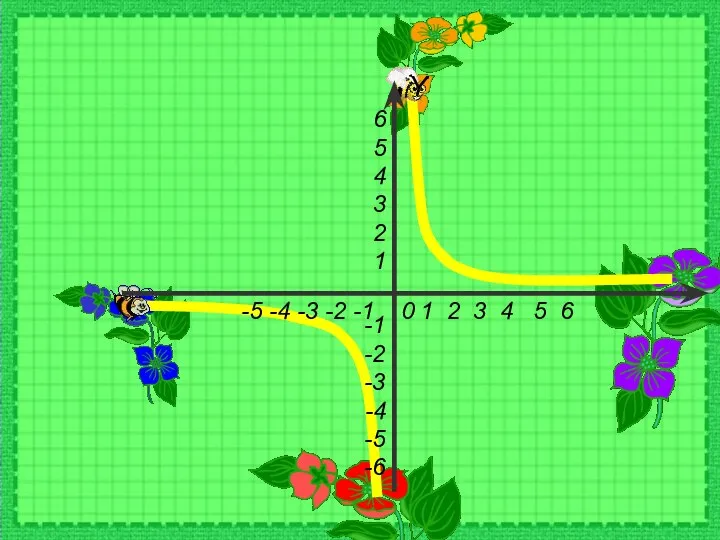 Функция у=1/х и её график
Функция у=1/х и её график Корни. Формулы
Корни. Формулы Вырезаем квадрат
Вырезаем квадрат Основные формулы для Огэ по математике
Основные формулы для Огэ по математике Решаем задачи
Решаем задачи Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Задачи с параметром в материалах ГИА и методы их решения (по материалам ЕГЭ за последние 5 лет)
Задачи с параметром в материалах ГИА и методы их решения (по материалам ЕГЭ за последние 5 лет) Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ Prezentado de enspezoj
Prezentado de enspezoj ДНФ и импликанты
ДНФ и импликанты Парная регрессия и корреляция
Парная регрессия и корреляция Первообразная и неопределённый интеграл. Лекция 2
Первообразная и неопределённый интеграл. Лекция 2