Содержание
- 2. План Разберём ДЗ Несколько слов о математическом моделировании. Функции 2-х переменных; функции многих переменных. Частные производные,
- 3. Разбор ДЗ по теме «Производные одной переменной»
- 7. Задание 2 = - sin(pi + 3*sqrt(pi))(2*sqrt(pi)+3) = = sin(3*sqrt(pi))(2*sqrt(pi)+3) = = -5,38 (с округлением)
- 8. Задание 3
- 10. Задание 4
- 11. Функции многих переменных. Где применяется математическое моделирование? Модели потребительского выбора, фирмы (производственные функции); экономического роста; равновесия
- 12. Математическое моделирование – зачем? Упрощенно описать реальность. Учесть ключевые факторы. Принять решение. Математическая модель – основа
- 13. Задачи математического программирования Решают: проблему выбора, оптимизации. У истоков: Канторович, Кун, Таккер.
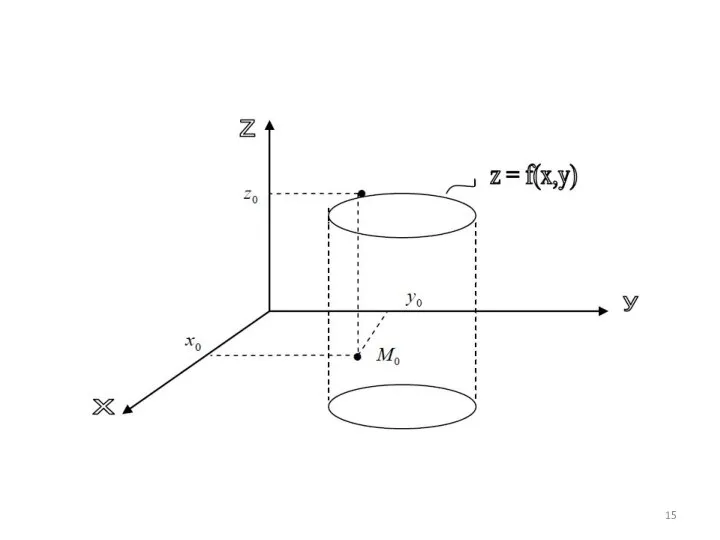
- 14. Функция 2-х переменных: определение. График функции - поверхность
- 16. Область определения функции 2-х переменных D(x;y)
- 17. Примеры поверхностей 2-го порядка
- 18. Пример
- 19. Пример
- 20. Пример Круг радиуса 1 в центре с началом координат D(x;y)
- 21. Функция многих переменных: определение.
- 22. Частные производные 1-го порядка - «дельта икс», приращение переменной x = - «дельта игрек», приращение переменной
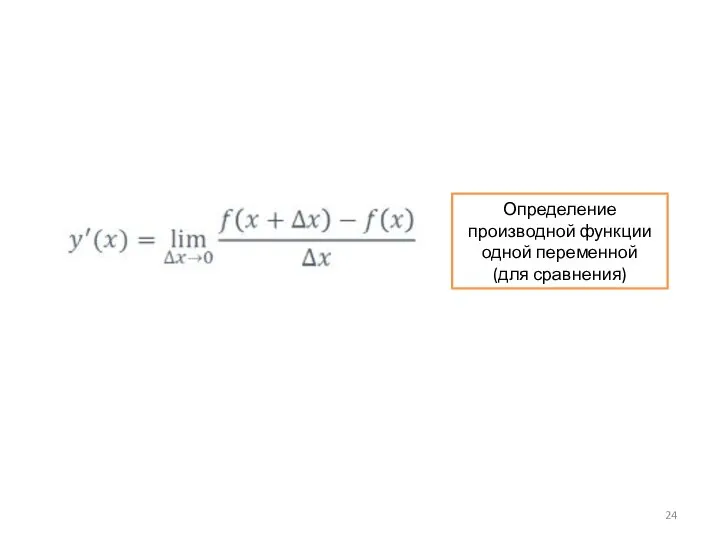
- 24. Определение производной функции одной переменной (для сравнения)
- 25. Вычисление частных производных
- 26. Сравнение с неявными функциями В случае неявной функции y зависит от х: y(x) В случае функции
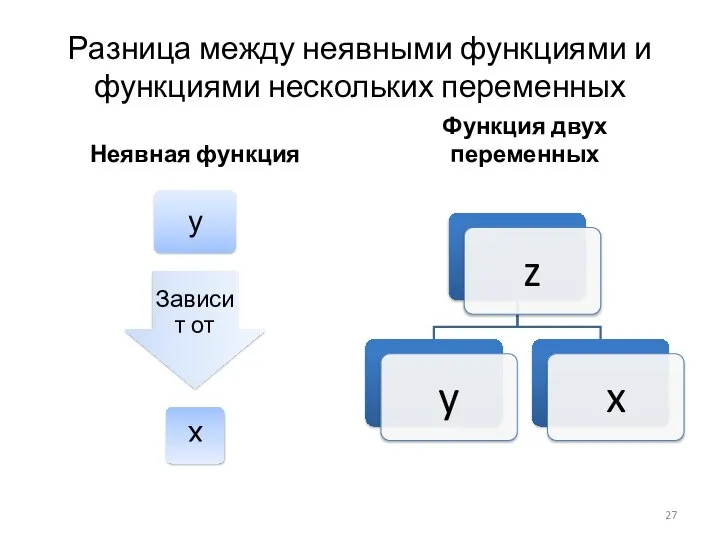
- 27. Разница между неявными функциями и функциями нескольких переменных Неявная функция Функция двух переменных
- 28. Вычислить:
- 29. Вычисление частных производных
- 31. Частный дифференциал функции многих переменных W(x,y,z) dx – «дифференциал икс» - произвольное бесконечно малое приращение переменной
- 32. Частный дифференциал не путаем с частной производной функции многих переменных Частный дифференциал равен частной производной умноженной
- 33. Полный дифференциал функции многих переменных W(x,y,z)
- 34. Полный дифференциал функции многих переменных W(x,y,z)
- 36. dW = W’(x)dx+W’(y)dy+W’(z)dz dW=(2cos(2x)+cos(5y))dx-5xsin(5y)dy-(7/(cos(7z)^2)dz dW(0;0;0)=3dx-7dz
- 37. dW (0;0;0) = 3dx-7dz Интерпретация В точке (0;0;0) при бесконечно малых приращениях x, y и z
- 38. Частные производные 2-го порядка
- 39. Частные производные 2-го порядка
- 47. Экстремум функции 2-х переменных
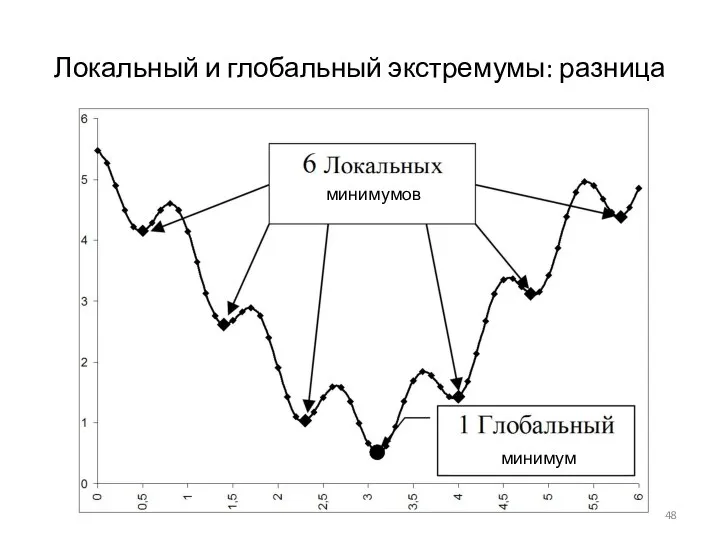
- 48. Локальный и глобальный экстремумы: разница минимумов минимум
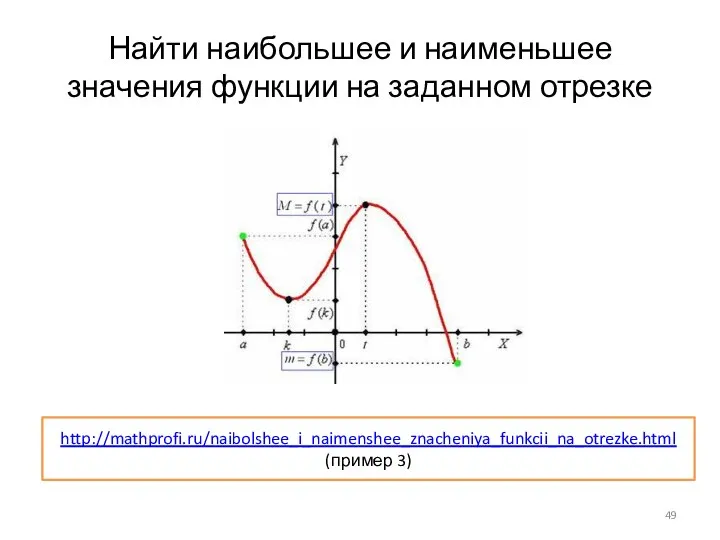
- 49. Найти наибольшее и наименьшее значения функции на заданном отрезке http://mathprofi.ru/naibolshee_i_naimenshee_znacheniya_funkcii_na_otrezke.html (пример 3)
- 50. Экстремум функции 2-х переменных Необходимые условия экстремума. Частные производные равны нулю или не существуют. Точки, для
- 51. Необходимые условия экстремума функции нескольких переменных z’x=0 z’y=0 (для стационарных точек)
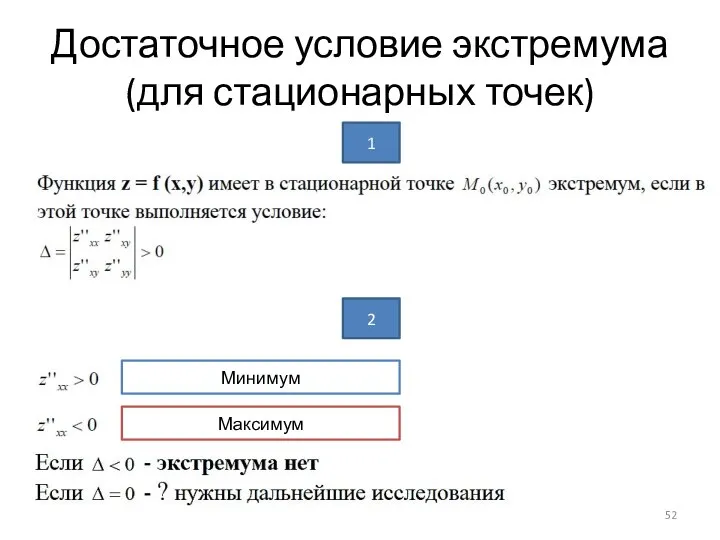
- 52. Достаточное условие экстремума (для стационарных точек) 1 2 Минимум Максимум
- 53. Определитель матрицы 2х2
- 54. К достаточному условию есть несколько подходов Два математических: через полный дифференциал второго порядка (требует большого навыка
- 55. Пример: исследовать на экстремум функцию
- 56. Необходимые условия
- 57. Достаточные условия (частный случай критерия Сильвестра) М1 (0;0) М2 (1;0.5)
- 58. Источник: www.linis.ru
- 59. Комментарий к записи
- 60. Аппроксимация
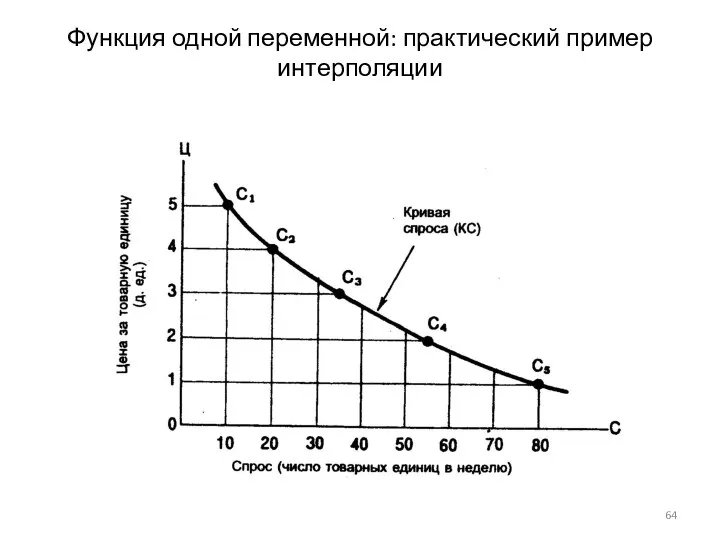
- 61. Интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Экстраполяция — способ
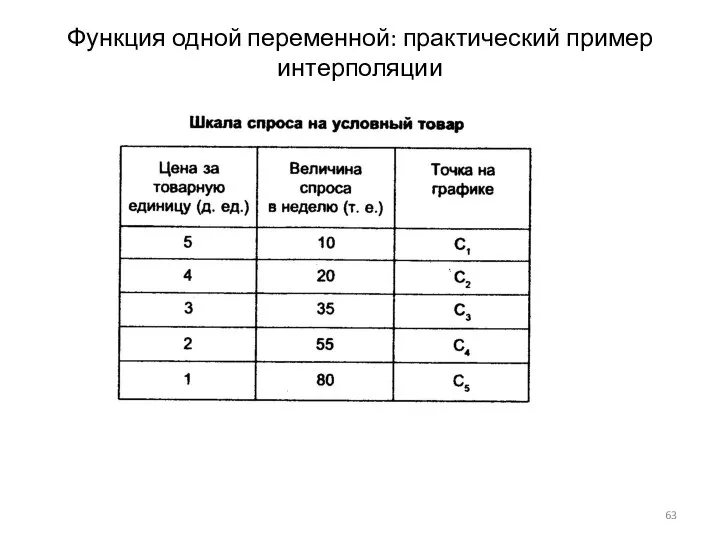
- 63. Функция одной переменной: практический пример интерполяции
- 64. Функция одной переменной: практический пример интерполяции
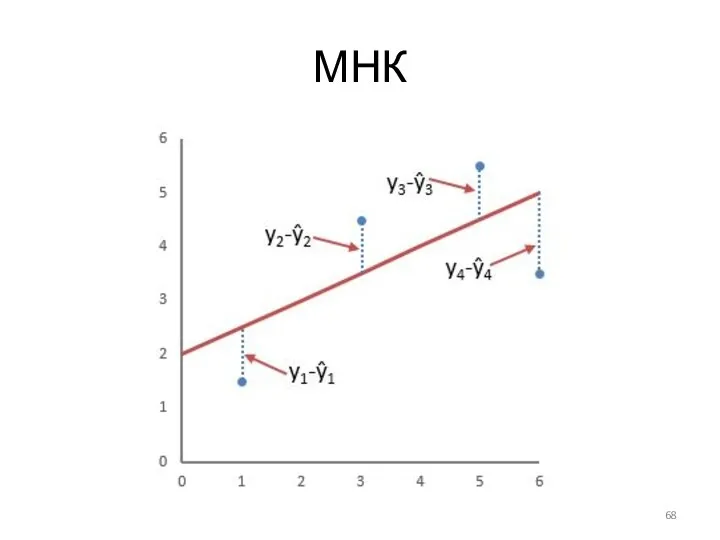
- 68. МНК
- 71. Оценка качества модели: коэффициент детерминации Находится в диапазоне от 0 до 1; Чем ближе к 1,
- 72. МНК для нелинейных функций Взвешенный МНК Обобщённый МНК И т. д.
- 73. МНК для нелинейных функций
- 74. МНК для нелинейных функций
- 76. Скачать презентацию


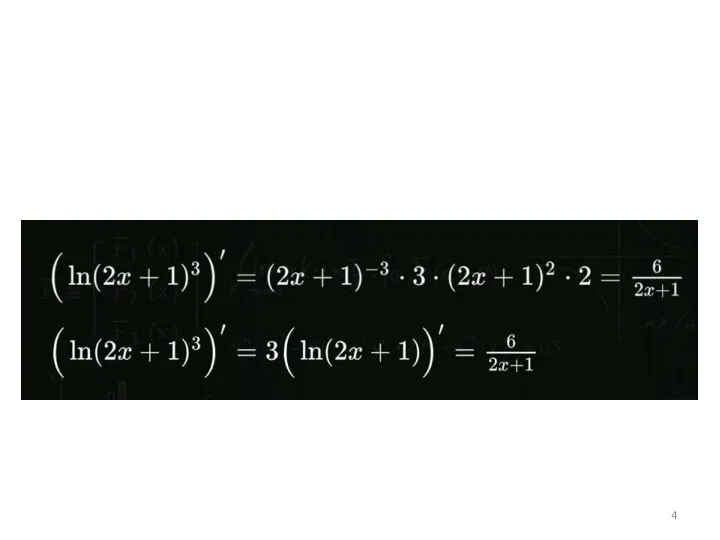




























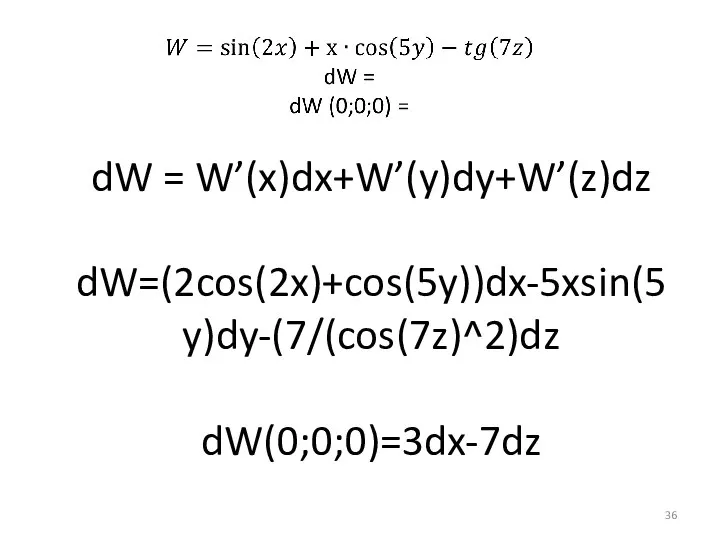



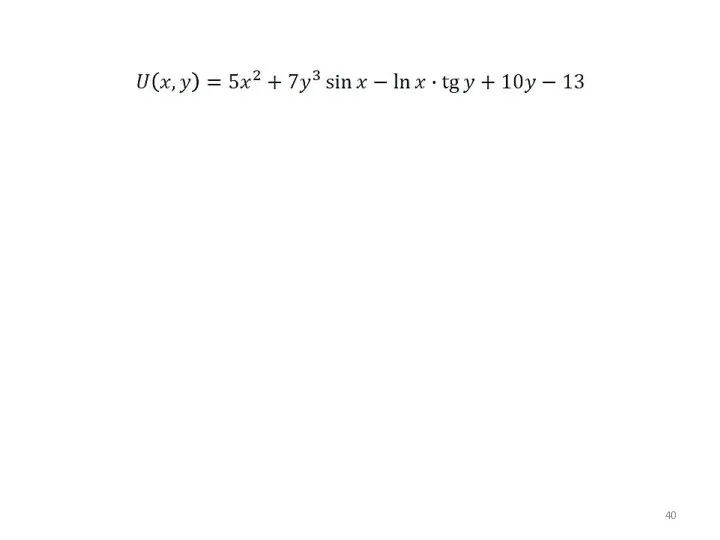
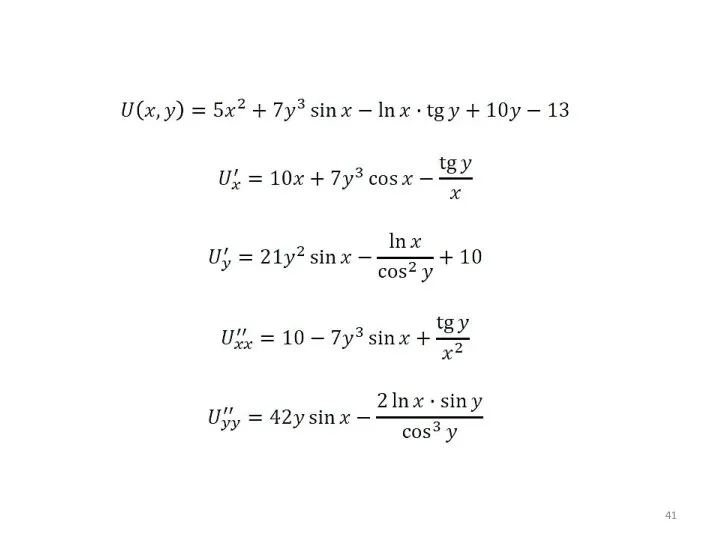
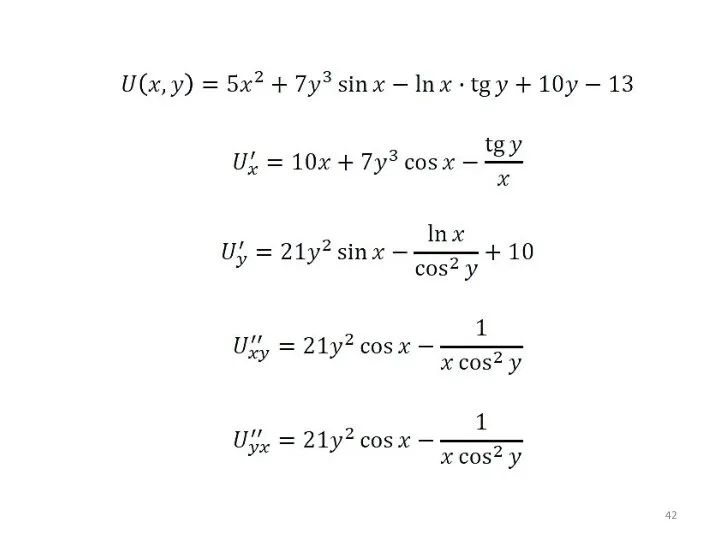
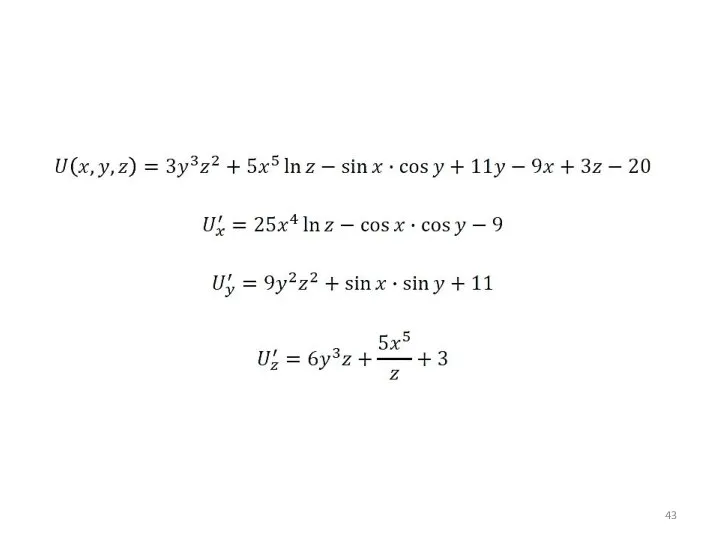
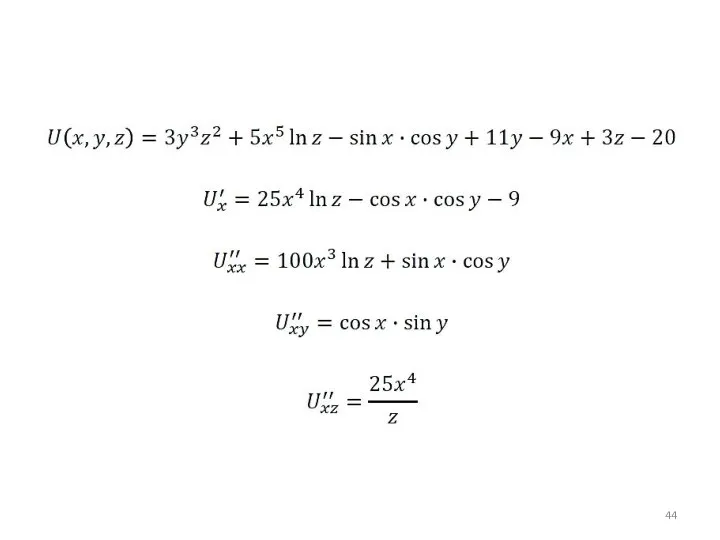
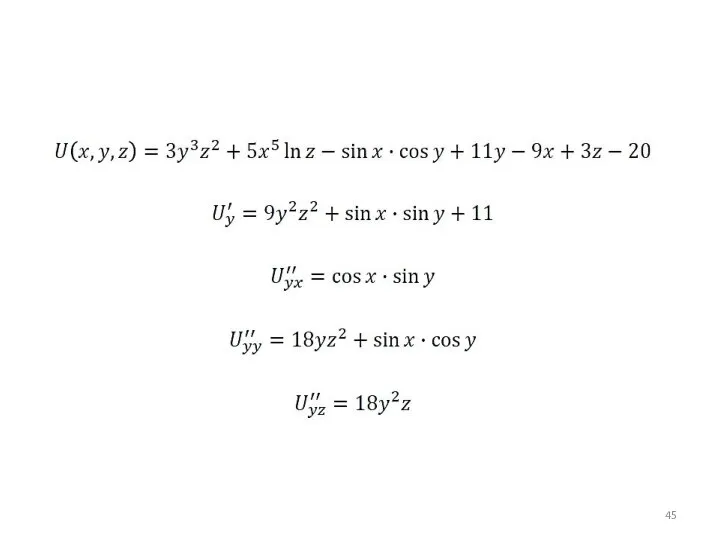
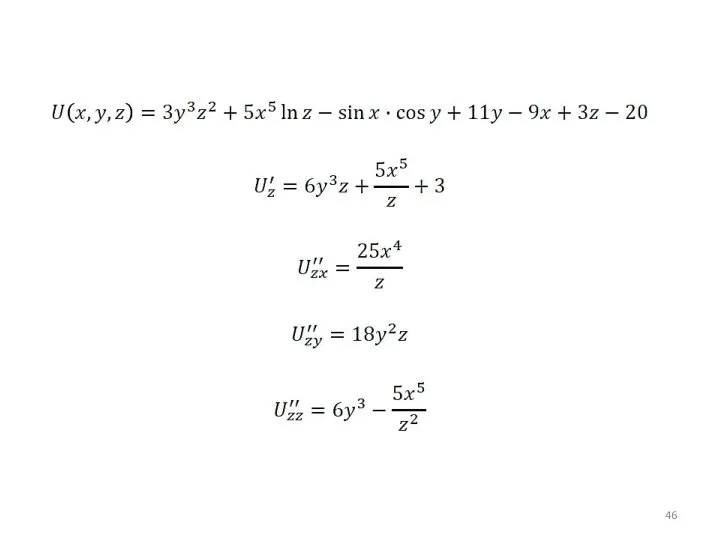
















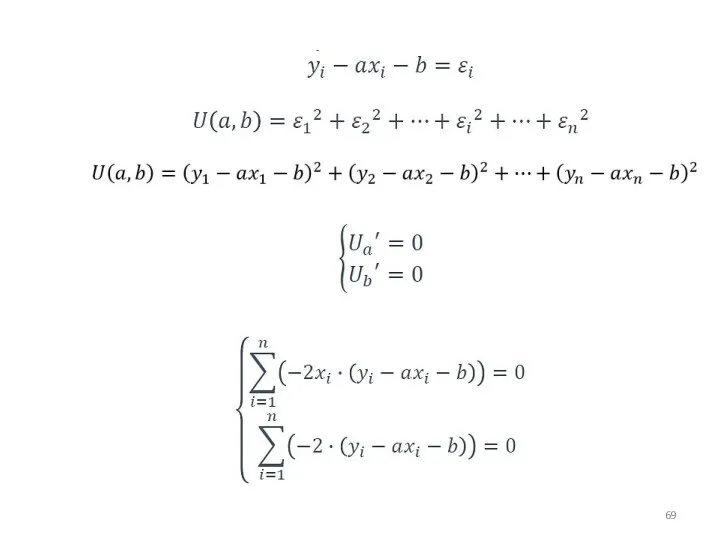





 Деление дробей
Деление дробей Сложение вида +6
Сложение вида +6 Длина окружности
Длина окружности Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Линейные однородные дифференциальные уравнения с постоянными коэффициентами Делим на равные части
Делим на равные части Тестовые задания
Тестовые задания Степень с натуральным показателем
Степень с натуральным показателем Определители второго и третьего порядка. 11 класс
Определители второго и третьего порядка. 11 класс Что такое проекция вектора
Что такое проекция вектора Проценты. Задачи на проценты
Проценты. Задачи на проценты Как построить график функции y=f(x)+m, если известен график функции y=f(x)
Как построить график функции y=f(x)+m, если известен график функции y=f(x) Функция
Функция Четные и нечётные функции
Четные и нечётные функции Область визначення функції
Область визначення функції Презентация на тему Дифференцирование частного и степени
Презентация на тему Дифференцирование частного и степени  Презентация на тему Грамм (3 класс)
Презентация на тему Грамм (3 класс)  Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс Умножение суммы на число
Умножение суммы на число Умножение величины на число
Умножение величины на число Сравнение числовых выражений
Сравнение числовых выражений Графический метод решения системы уравнений с двумя переменными
Графический метод решения системы уравнений с двумя переменными Умножение
Умножение Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Презентация на тему Квадратный трёхчлен и его приложения
Презентация на тему Квадратный трёхчлен и его приложения  Решение задач, 1 класс
Решение задач, 1 класс Производная функции. Решения
Производная функции. Решения Математика. Решение задач
Математика. Решение задач Подготовка к ГИА. 9 класс
Подготовка к ГИА. 9 класс