Содержание
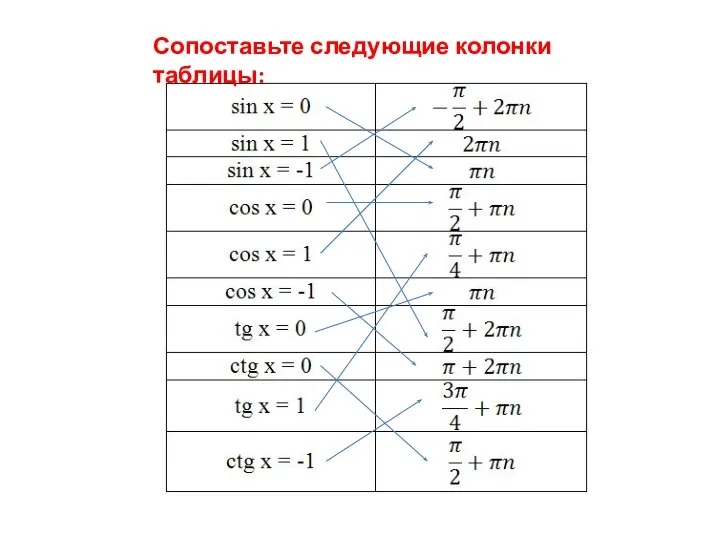
- 2. Сопоставьте следующие колонки таблицы:
- 3. Решить уравнения: 1). Решение: Ответ: 2). Решение: Ответ:
- 4. 3) ООУ: Решение: Ответ:
- 5. Метод введения вспомогательной переменной. №1. Решение: Замена: Не имеет решений Ответ:
- 6. №2. Решение: Не имеет решений Ответ: Воспользуемся формулой: Получаем:
- 7. Метод разложения на множители. №3. Решение: О.О.У.: Данное решение не удовлетворяет О.О.У. Ответ: . Сгруппируем слагаемые
- 8. № 4 Решение: Воспользуемся формулой разности косинусов: Не имеет решений Ответ:
- 9. Однородные уравнения. №5 Решение: данная система не имеет решений Следовательно, cos x = 0 не является
- 10. № 6 3sin 2 x + 4 sin x · cos x + 5 cos 2
- 11. Неоднородные уравнения. № 7 Решение: Поделим обе части уравнения на Получим уравнение Замечаем, что , т.е.
- 12. Решение: Поделим обе части уравнения на Получим уравнение Замечаем, что , т.е. имеем уравнение: В данном
- 14. Скачать презентацию










 Характер и ритм линий как средство выражения
Характер и ритм линий как средство выражения Задачи по геометрии
Задачи по геометрии Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе
Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве Урок-игра. Пик знаний.Тригонометрически функции
Урок-игра. Пик знаний.Тригонометрически функции Окружность. Вписанные углы
Окружность. Вписанные углы Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Метрическая система мер
Метрическая система мер Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) Преобразование тригонометрических графиков
Преобразование тригонометрических графиков Математика и мир искусства
Математика и мир искусства Дискретная математика. Задание №2. Матрица инцидентности неориентированного графа
Дискретная математика. Задание №2. Матрица инцидентности неориентированного графа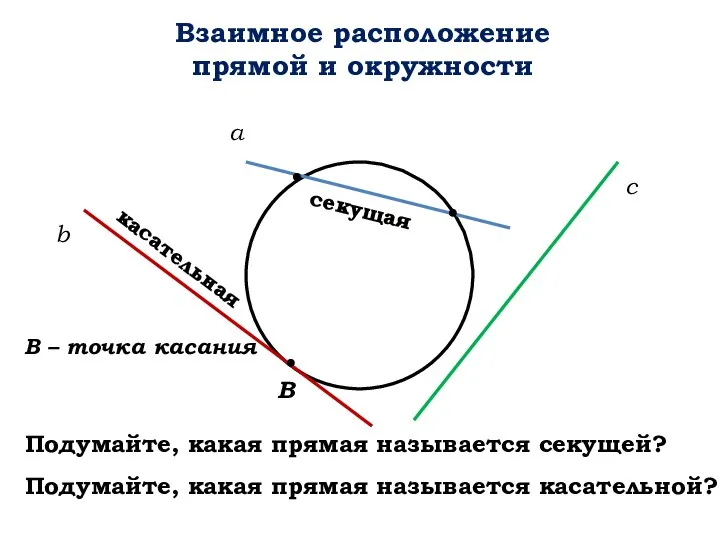 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Производная и первообразная
Производная и первообразная Презентация на тему ИСКУССТВО РАССУЖДАТЬ
Презентация на тему ИСКУССТВО РАССУЖДАТЬ  Презентация на тему Урок по теме «Координатная плоскость» 6 класс
Презентация на тему Урок по теме «Координатная плоскость» 6 класс  Отношения и золотое сечение
Отношения и золотое сечение Подготовка к ГИА. Алгебраические выражения. Часть 1
Подготовка к ГИА. Алгебраические выражения. Часть 1 Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Задачи на нахождение неизвестного слагаемого
Задачи на нахождение неизвестного слагаемого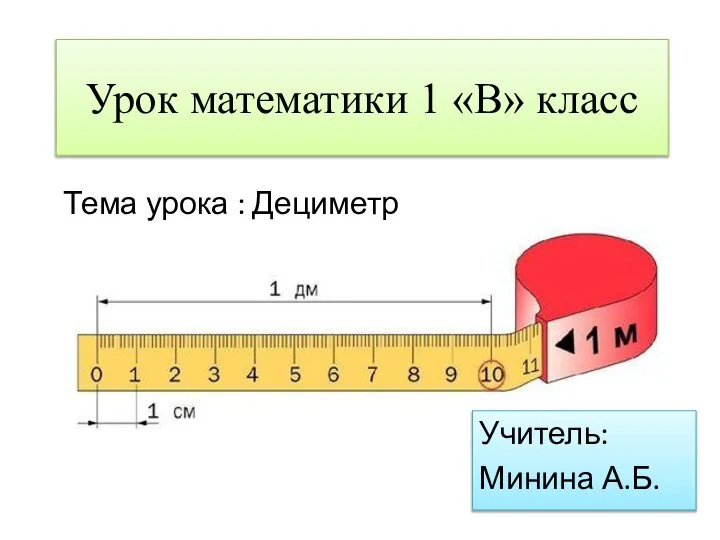 Дециметр
Дециметр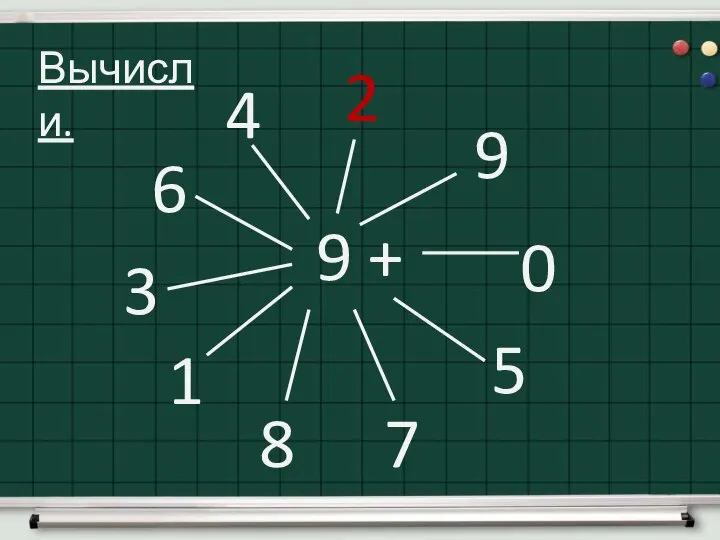 Повторение. Математика, 1 класс
Повторение. Математика, 1 класс Элементы теории вероятности
Элементы теории вероятности Построение сечений многогранников
Построение сечений многогранников Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Задание 4. Числа, вычисления и алгебраические выражения
Задание 4. Числа, вычисления и алгебраические выражения Предел функции (часть 4)
Предел функции (часть 4)