Содержание
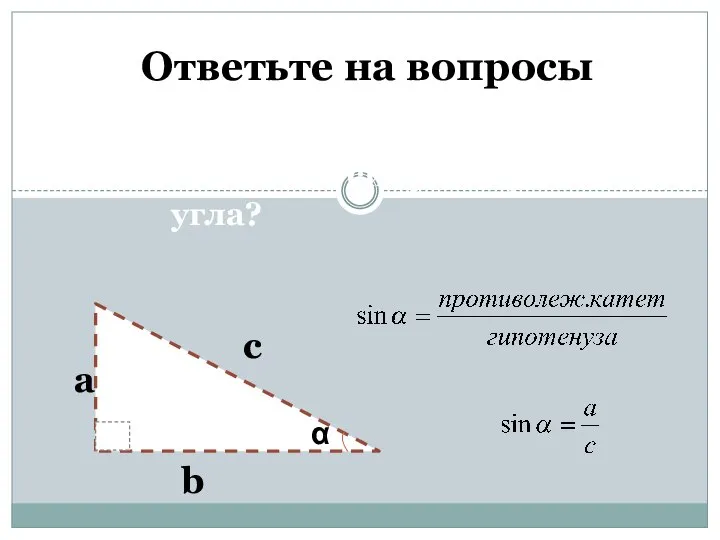
- 2. Ответьте на вопросы Что такое синус острого угла? b а с α
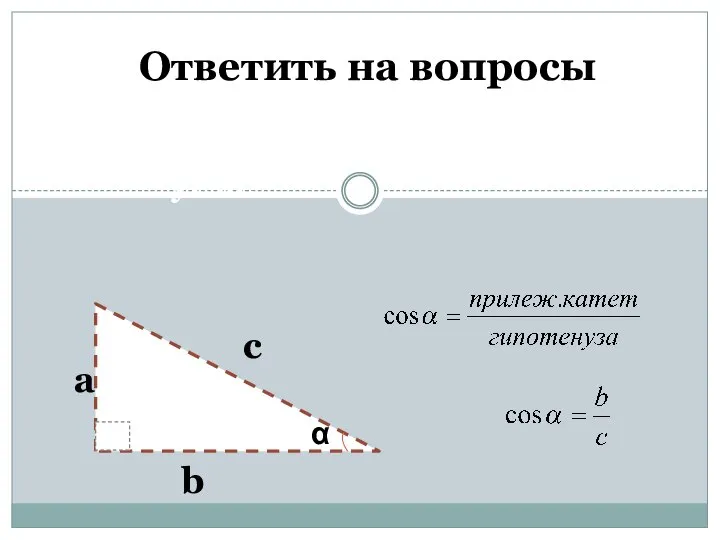
- 3. Ответить на вопросы 2. Что такое косинус острого угла? b а с α
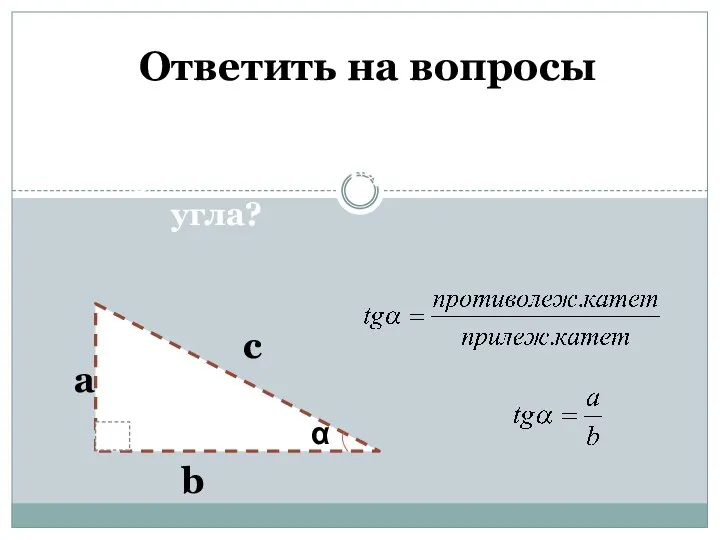
- 4. Ответить на вопросы 3. Что такое тангенс острого угла? b а с α
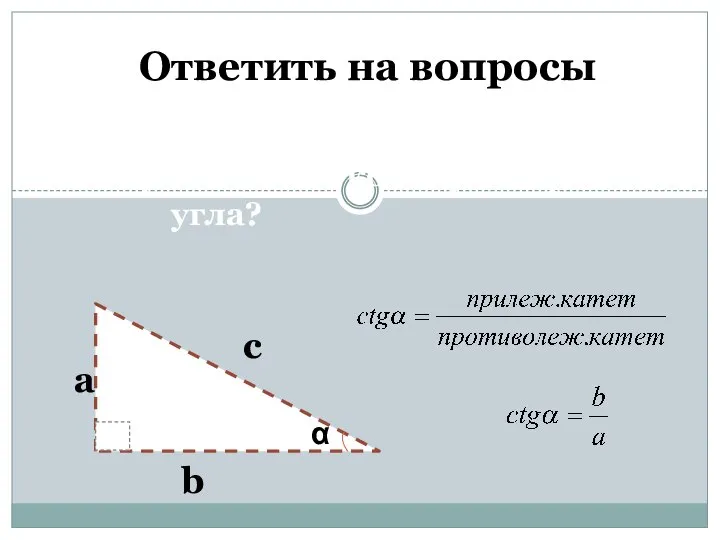
- 5. Ответить на вопросы 4. Что такое косинус острого угла? b а с α
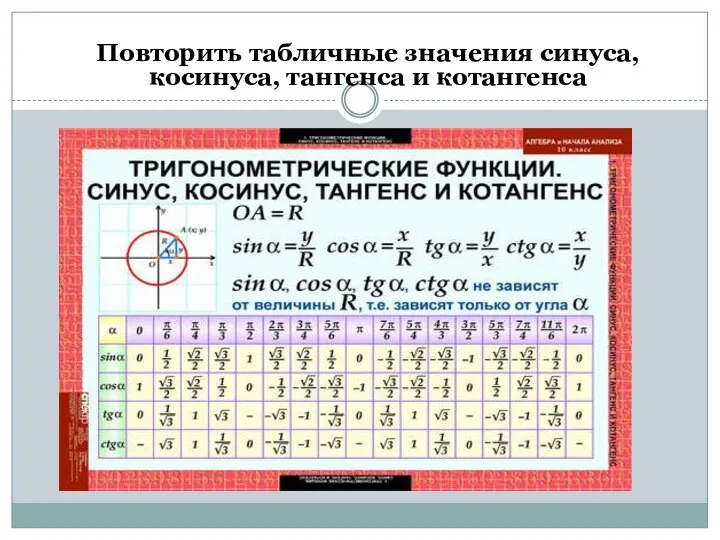
- 6. Повторить табличные значения синуса, косинуса, тангенса и котангенса
- 7. Выполните тест Табличные значения синуса, косинуса. Тангенса и котангенса 1. Sin 60⁰ =…. а) , б)
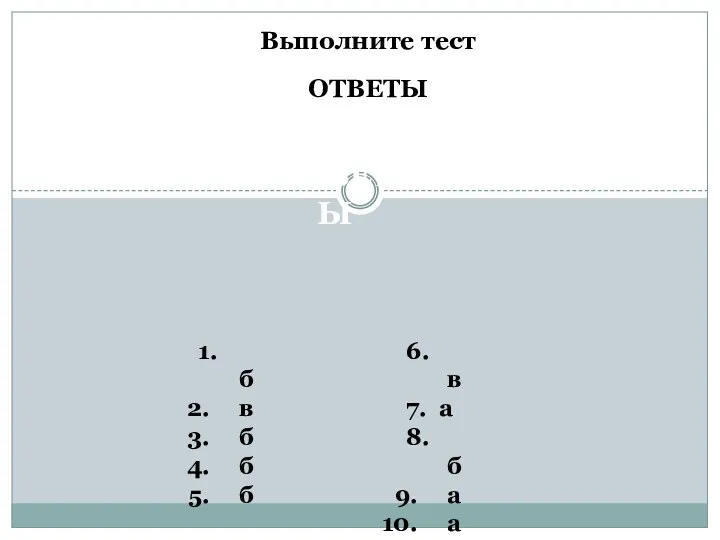
- 8. Выполните тест ОТВЕТЫ ОТВЕТЫ 1. б в б б б 6. в 7. а 8. б
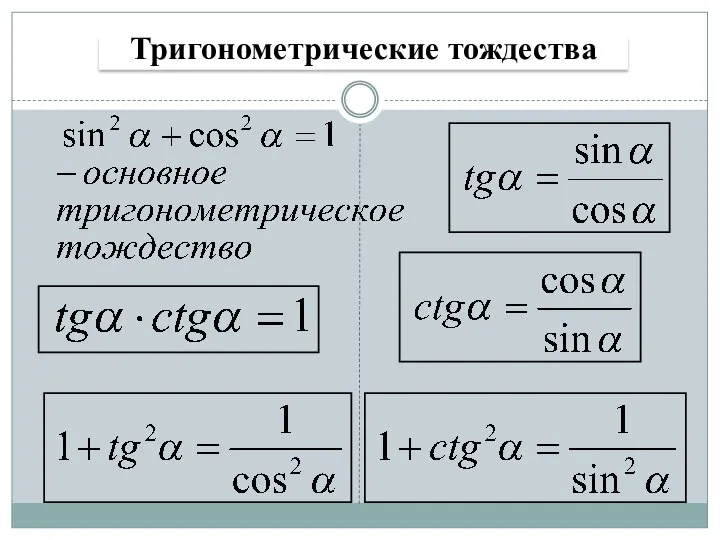
- 9. Тригонометрические тождества
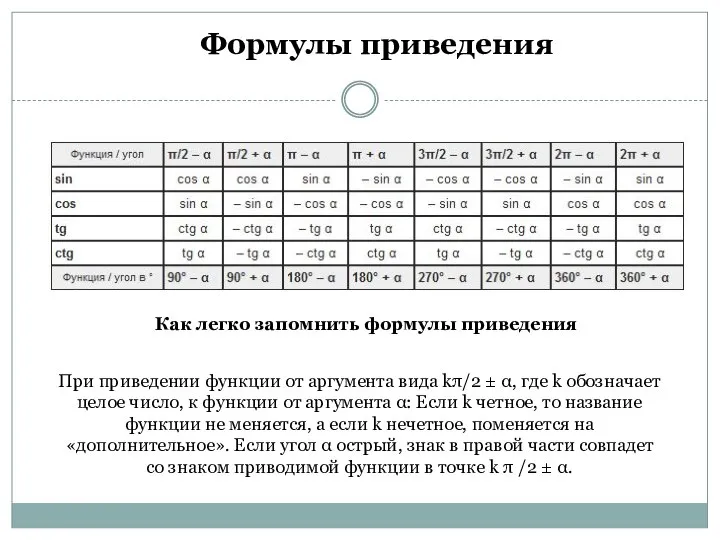
- 10. Формулы приведения sin ( 90⁰ + α) = cos α; cos ( 90 + α) =
- 11. Формулы приведения При приведении функции от аргумента вида kπ/2 ± α, где k обозначает целое число,
- 12. Формулы приведения
- 13. Пример 1 Ответ:
- 15. Скачать презентацию




 Векторы. 9 класс
Векторы. 9 класс Формула объема пирамиды
Формула объема пирамиды Формування математчних моделей електронних кіл
Формування математчних моделей електронних кіл Задача о баскетболисте. Расчетная работа №1
Задача о баскетболисте. Расчетная работа №1 Тригонометрические уравнения Однородные тригонометрические уравнения
Тригонометрические уравнения Однородные тригонометрические уравнения Все действия с рациональными дробями. Подготовка к контрольной работе
Все действия с рациональными дробями. Подготовка к контрольной работе Формула у=х2
Формула у=х2 Многочлен. Стандартный вид многочлена. Степень многочлена
Многочлен. Стандартный вид многочлена. Степень многочлена Официальная статистика как условие устойчивого развития сельского хозяйства
Официальная статистика как условие устойчивого развития сельского хозяйства Геометрия. Построение
Геометрия. Построение Евклидова геометрия
Евклидова геометрия Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем Измерение площади с помощью палетки. 4 класс
Измерение площади с помощью палетки. 4 класс Вторая производная и ее физический смысл
Вторая производная и ее физический смысл Отношения и пропорция
Отношения и пропорция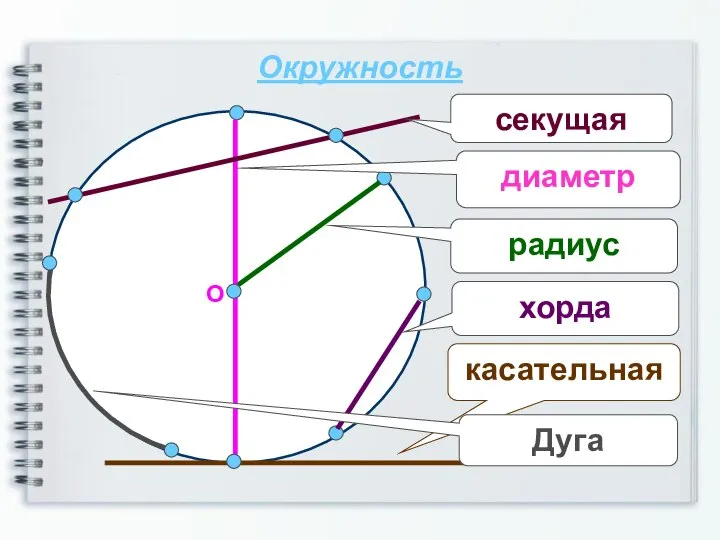 Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1)
Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1) Теорема о площади треугольников
Теорема о площади треугольников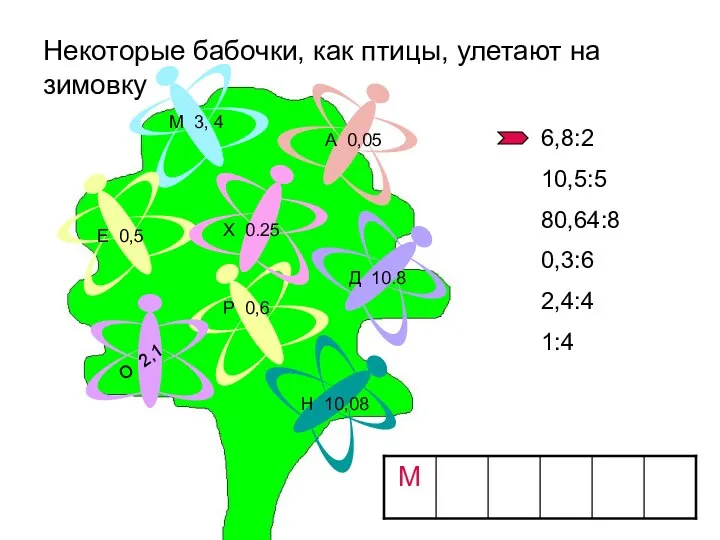 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку Тела вращения. Урок 142
Тела вращения. Урок 142 Веселая математика. Головоломки
Веселая математика. Головоломки Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Методы расчета КИХ-фильтров
Методы расчета КИХ-фильтров Коррекция нелинейных систем
Коррекция нелинейных систем Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Урок математики во 2 классе «Устные приемы вычислений в пределах 100» Выполнила: учитель начальных классов МОУ «СОШ № 43» Города Са
Урок математики во 2 классе «Устные приемы вычислений в пределах 100» Выполнила: учитель начальных классов МОУ «СОШ № 43» Города Са Решение неполных квадратных уравнений
Решение неполных квадратных уравнений Планирование эксперимента
Планирование эксперимента Консультация ДУ
Консультация ДУ