Содержание
- 2. Тема: Основы теории статистических показателей Статистический показатель, понятие, функции, формы Абсолютные статистические величины Относительные статистические величины
- 3. 1. Статистический показатель, понятие, функции, формы Статистический показатель – важнейшая категория статистики, ее язык. Он представляет
- 4. Статистические показатели выполняют ряд функций: познавательную (гносеологическую) управленческую прогностическую оценочную рекламно-пропагандистскую.
- 5. «Считают, будто числа управляют миром. Но я знаю, что числа учат нас узнавать, хорошо ли мир
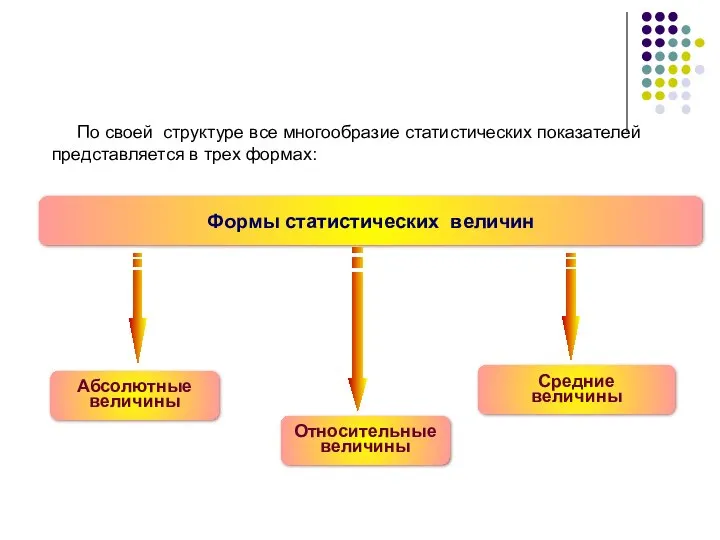
- 6. Формы статистических величин Абсолютные величины Относительные величины Средние величины По своей структуре все многообразие статистических показателей
- 7. 2. Абсолютные статистические величины Материалы статистического наблюдения обобщаются прежде всего в форме абсолютных статистических величин. Абсолютная
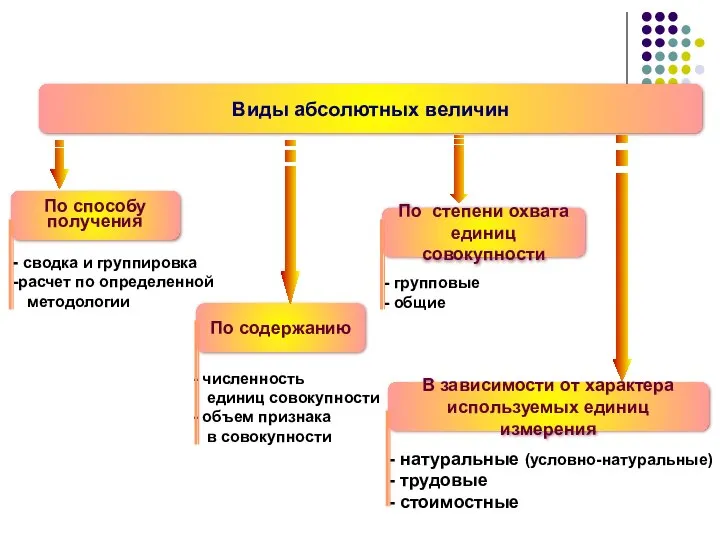
- 8. Виды абсолютных величин По способу получения По содержанию По степени охвата единиц совокупности В зависимости от
- 9. ПРИМЕРЫ
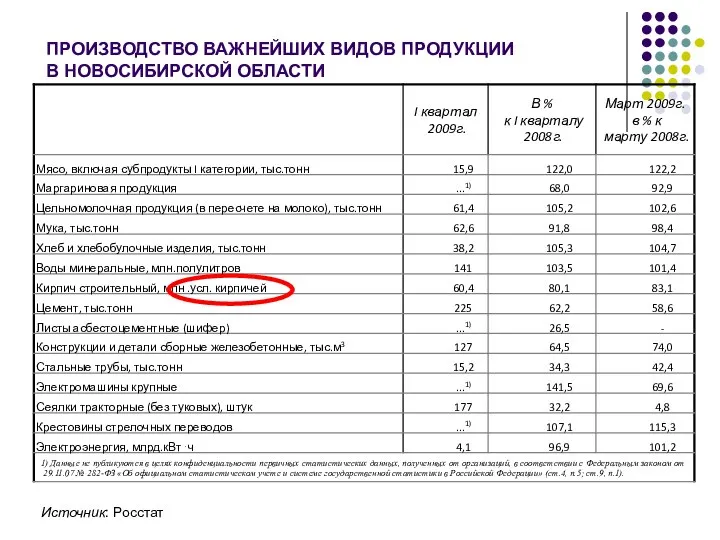
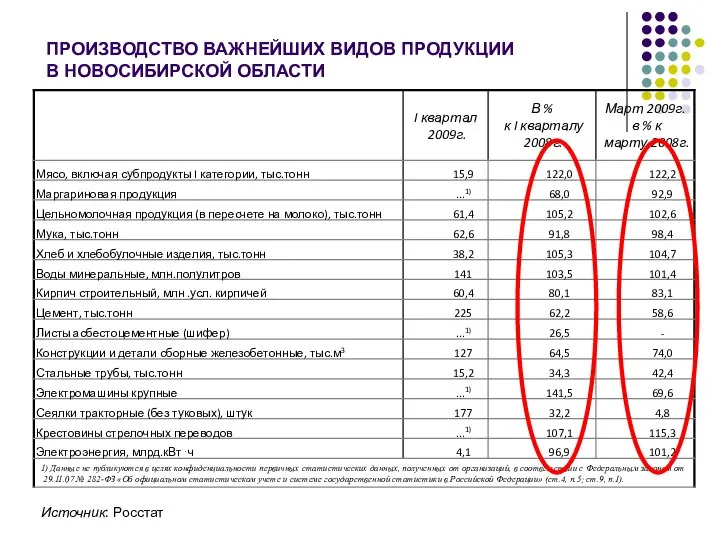
- 10. ПРОИЗВОДСТВО ВАЖНЕЙШИХ ВИДОВ ПРОДУКЦИИ В НОВОСИБИРСКОЙ ОБЛАСТИ Источник: Росстат
- 11. Условно-натуральные единицы измерения
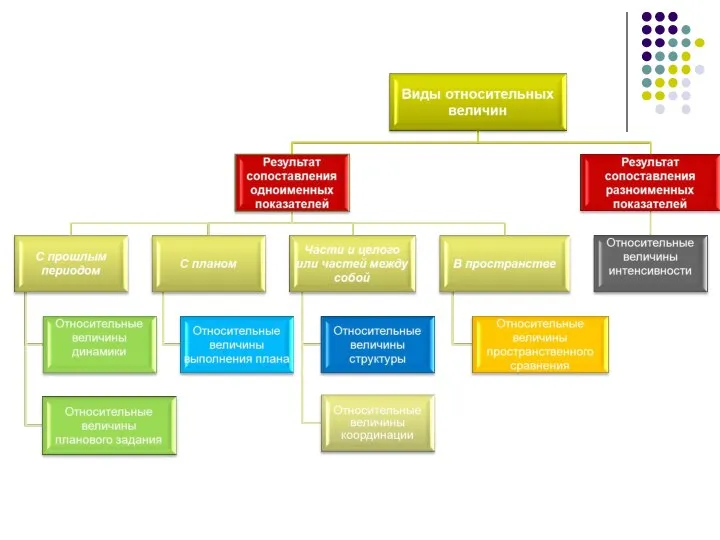
- 12. 3. Относительные статистические величины Под относительной величиной в статистике понимают количественно-качественную меру, выражающую соотношение между двумя
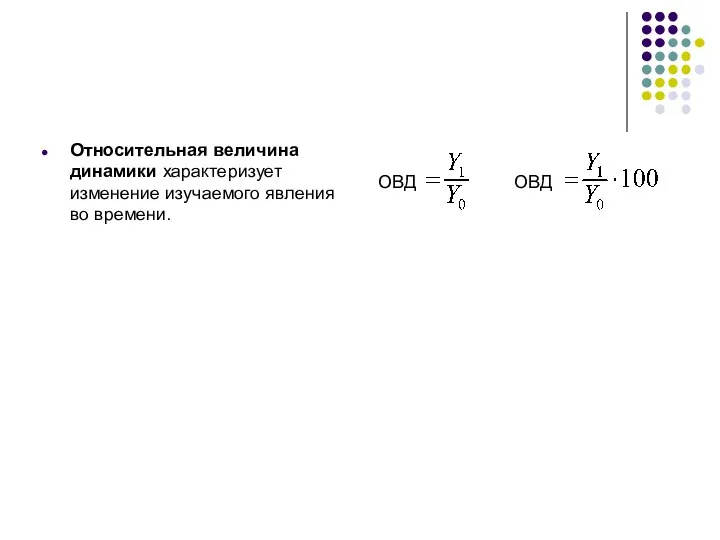
- 14. Относительная величина динамики характеризует изменение изучаемого явления во времени. ОВД ОВД
- 15. ПРОИЗВОДСТВО ВАЖНЕЙШИХ ВИДОВ ПРОДУКЦИИ В НОВОСИБИРСКОЙ ОБЛАСТИ Источник: Росстат
- 16. Относительная величина планового задания выражает относительную оценку намерений (ожиданий, перспектив) по развитию явления. Относительная величина выполнения
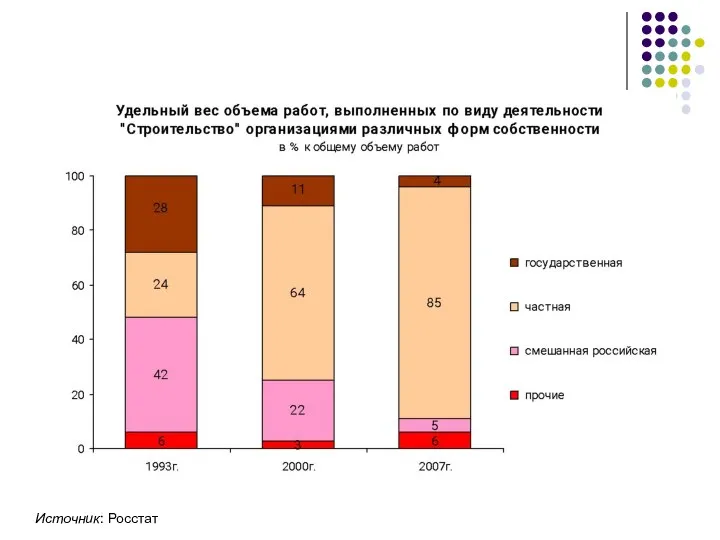
- 17. Относительная величина структуры характеризует состав изучаемой статистической совокупности. По объему признака в совокупности По числу единиц
- 18. Источник: Росстат
- 19. Относительная величина координации выражает соотношение между отдельными частями статистической совокупности. По объему признака в совокупности По
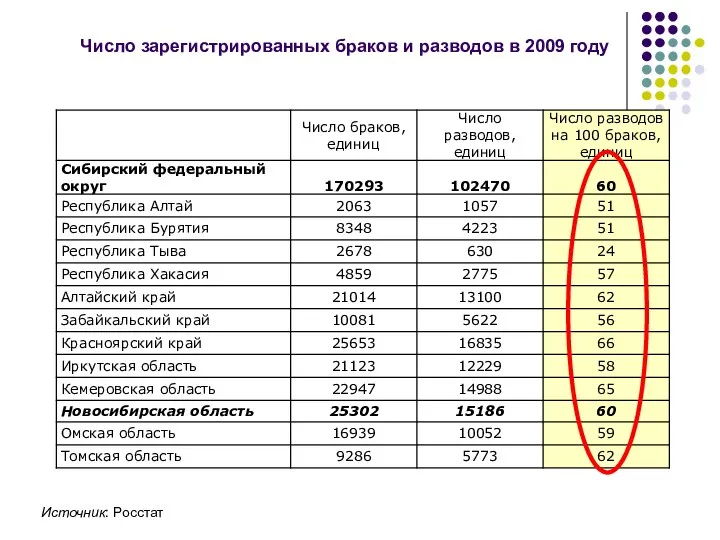
- 20. Число зарегистрированных браков и разводов в 2009 году Источник: Росстат
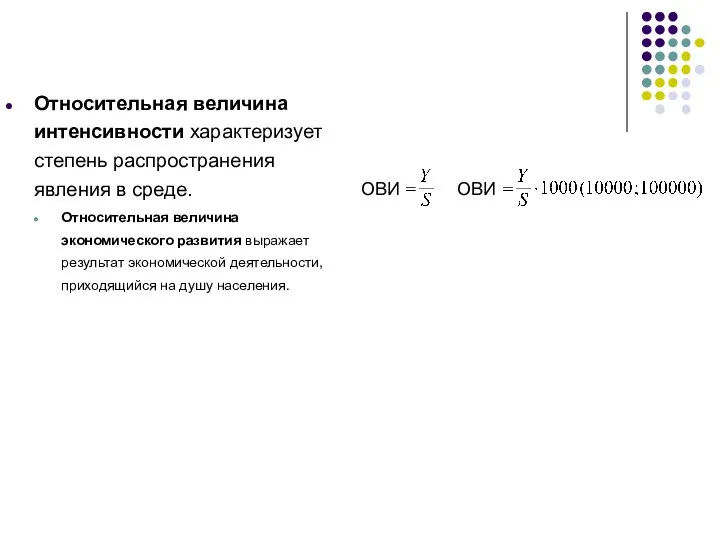
- 21. Относительная величина интенсивности характеризует степень распространения явления в среде. Относительная величина экономического развития выражает результат экономической
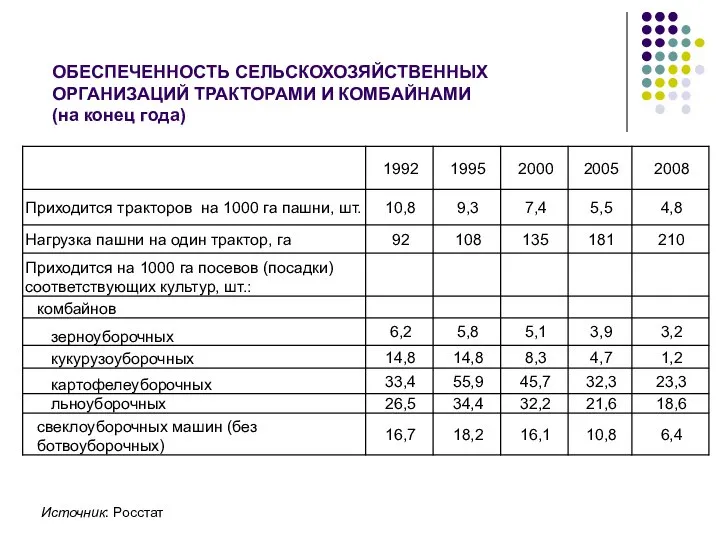
- 22. ОБЕСПЕЧЕННОСТЬ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ОРГАНИЗАЦИЙ ТРАКТОРАМИ И КОМБАЙНАМИ (на конец года) Источник: Росстат
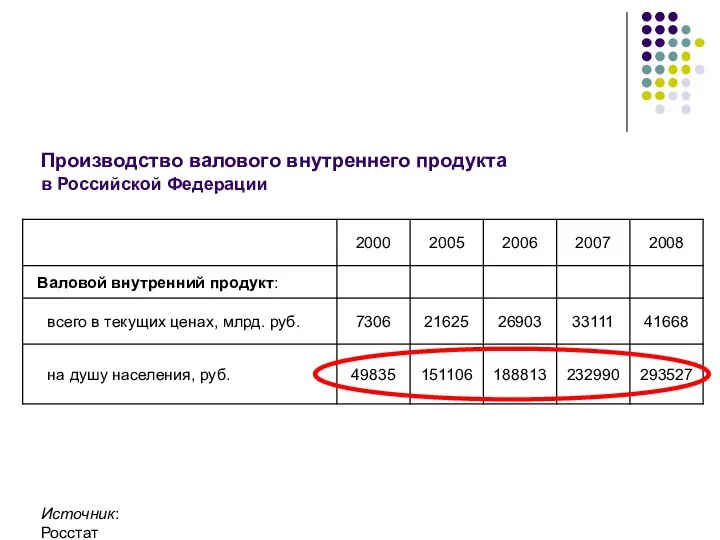
- 23. Производство валового внутреннего продукта в Российской Федерации Источник: Росстат
- 24. Относительная величина пространственного сравнения характеризует количественное соотношение одноименных показателей, относящихся к различным территориям (пространственным единицам). ОВПС
- 25. Укажите, к какому виду относительных величин по содержанию выражаемых количественных соотношений относятся следующие показатели: В 2007
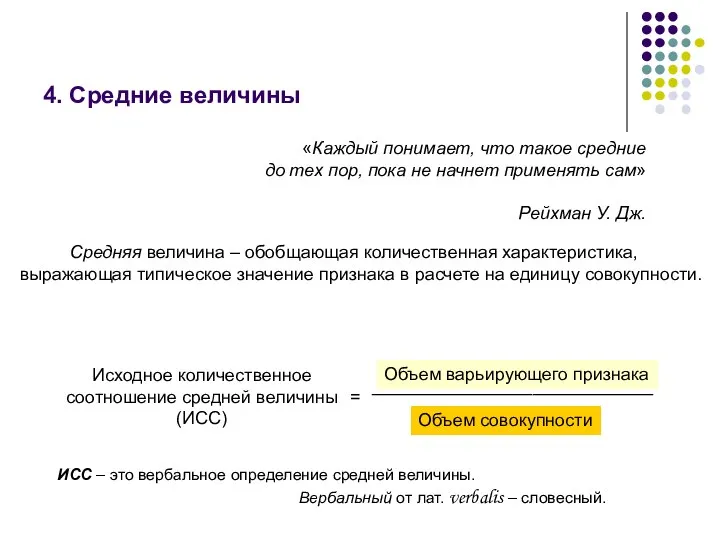
- 26. 4. Средние величины «Каждый понимает, что такое средние до тех пор, пока не начнет применять сам»
- 27. ОСНОВНЫЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЕ ИНДИКАТОРЫ УРОВНЯ ЖИЗНИ НАСЕЛЕНИЯ РОССИИ Источник: Росстат
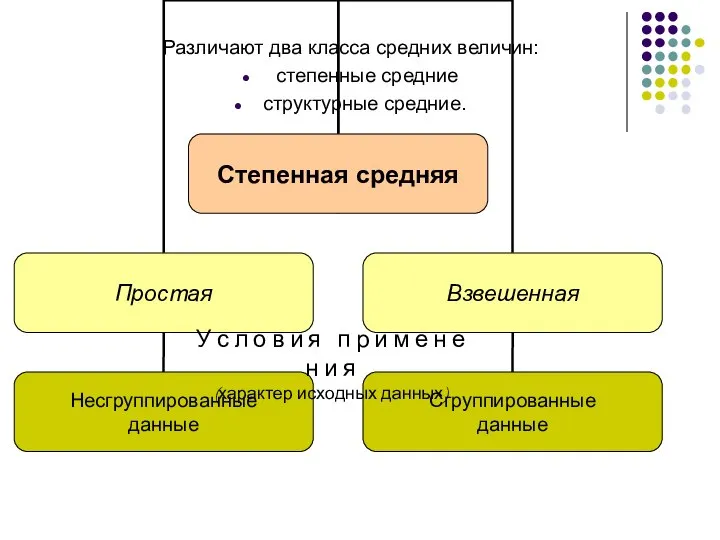
- 28. Различают два класса средних величин: степенные средние структурные средние. У с л о в и я
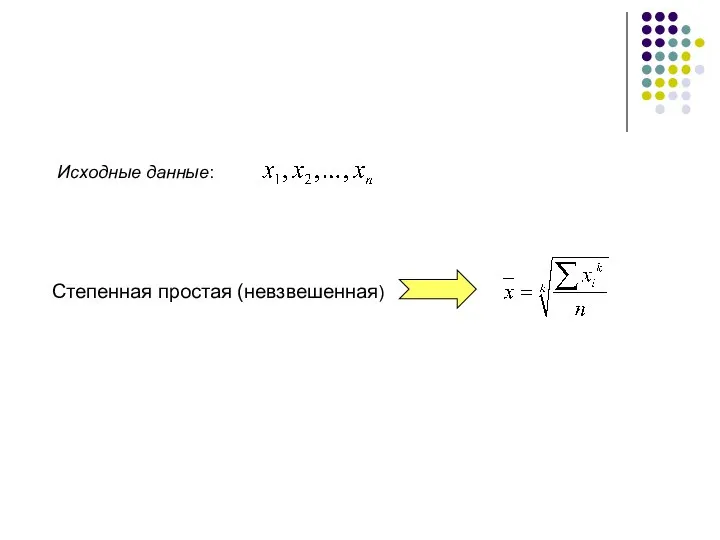
- 29. Степенная простая (невзвешенная) Исходные данные:
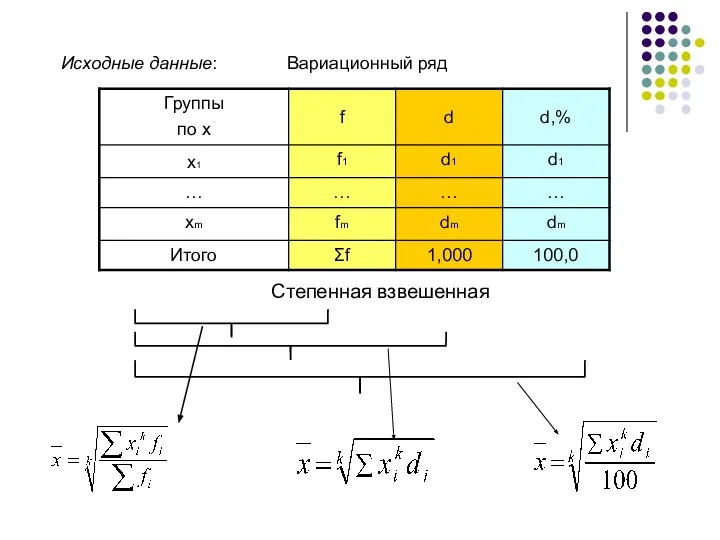
- 30. Степенная взвешенная Исходные данные: Вариационный ряд
- 31. Степенные средние Теоретически показатель степени k может быть любым. На практике степенные средние используют с показателем
- 32. Правило мажорантности средних
- 33. ПРИМЕРЫ
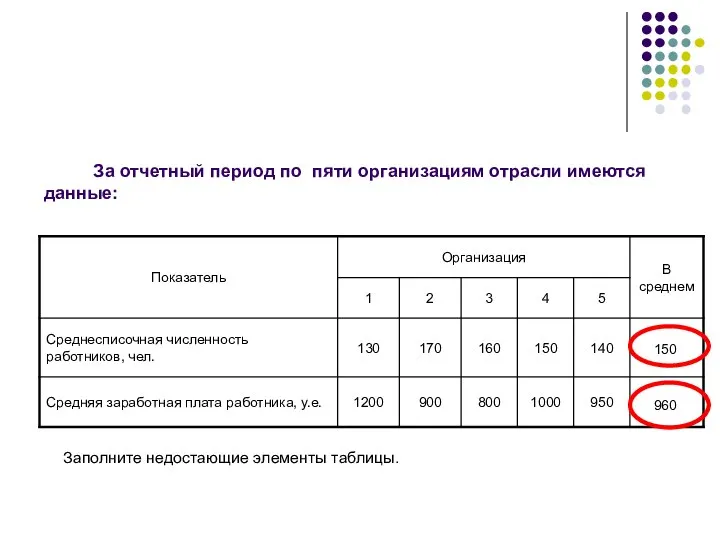
- 34. За отчетный период по пяти организациям отрасли имеются данные: Заполните недостающие элементы таблицы. 150 960
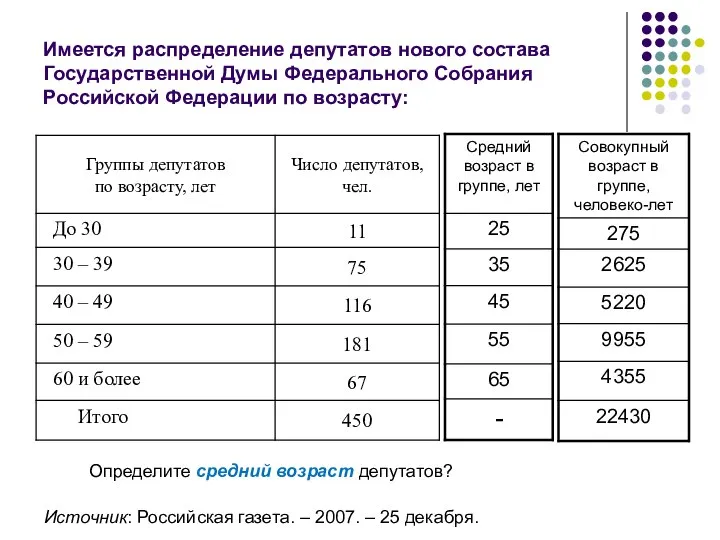
- 35. Имеется распределение депутатов нового состава Государственной Думы Федерального Собрания Российской Федерации по возрасту: Источник: Российская газета.
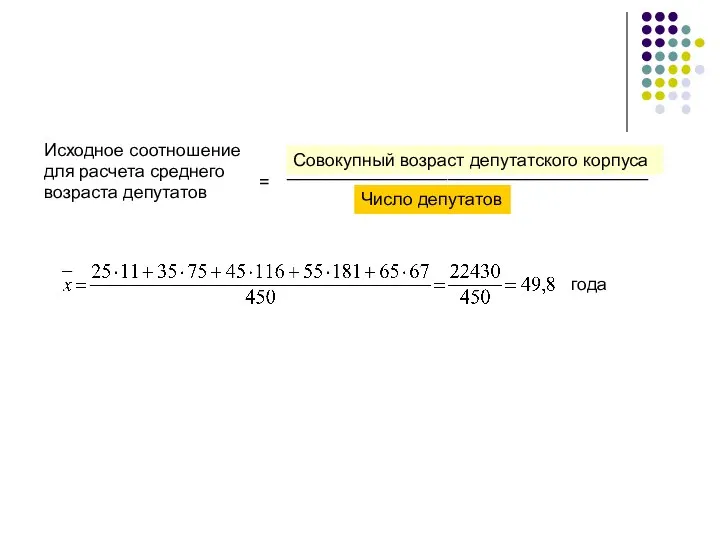
- 36. Исходное соотношение для расчета среднего возраста депутатов = ____________________________________ Совокупный возраст депутатского корпуса Число депутатов года
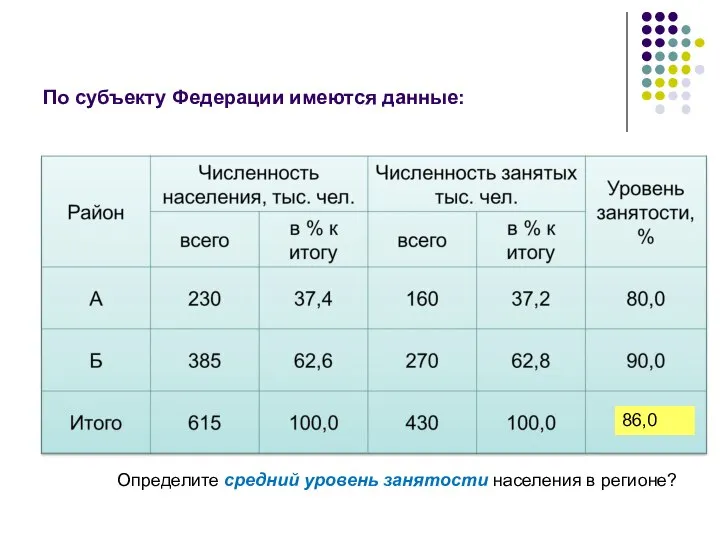
- 37. По субъекту Федерации имеются данные: 86,0 Определите средний уровень занятости населения в регионе?
- 38. Уровень занятости в регионе = -----------------------------------------------------------------------*100 = Численность занятых Численность экономически активного населения = % Уровень
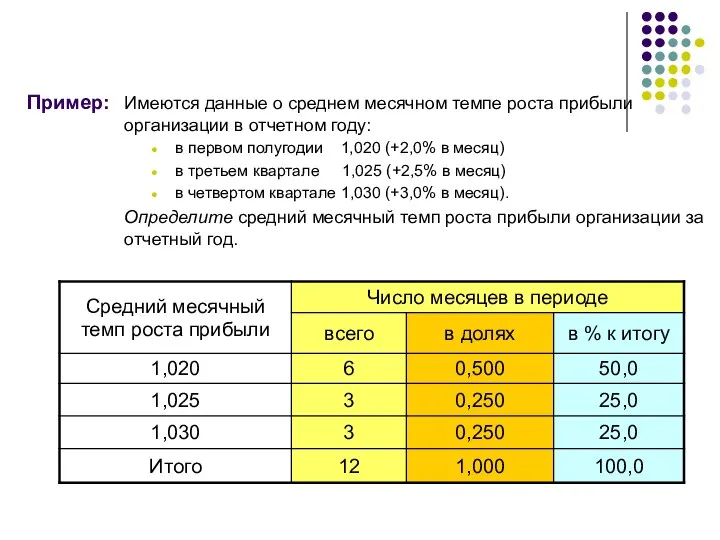
- 39. Пример: Имеются данные о среднем месячном темпе роста прибыли организации в отчетном году: в первом полугодии
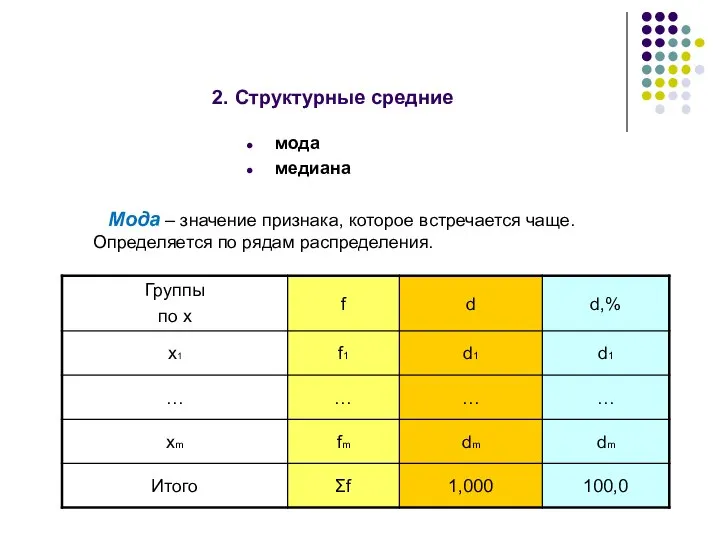
- 41. 2. Структурные средние мода медиана Мода – значение признака, которое встречается чаще. Определяется по рядам распределения.
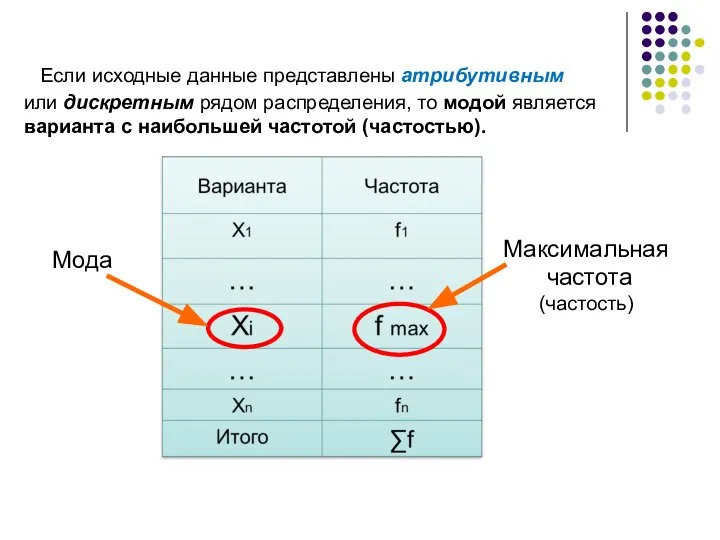
- 42. Если исходные данные представлены атрибутивным или дискретным рядом распределения, то модой является варианта с наибольшей частотой
- 43. ПРИМЕРЫ
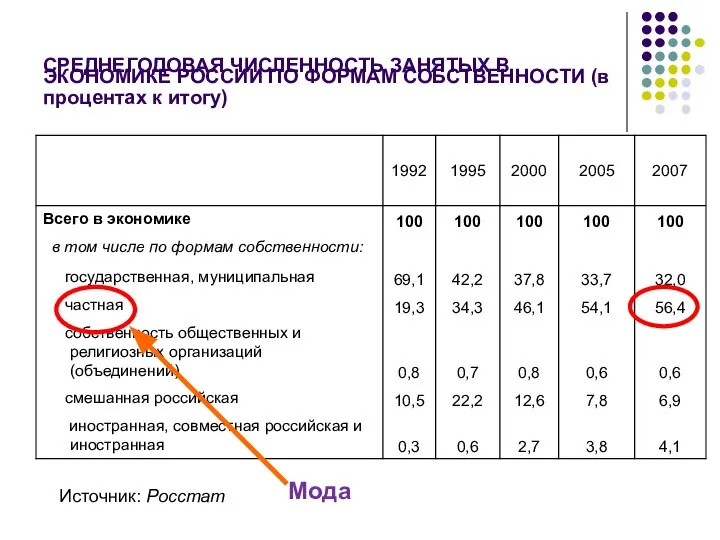
- 44. СРЕДНЕГОДОВАЯ ЧИСЛЕННОСТЬ ЗАНЯТЫХ В ЭКОНОМИКЕ РОССИИ ПО ФОРМАМ СОБСТВЕННОСТИ (в процентах к итогу) Источник: Росстат Мода
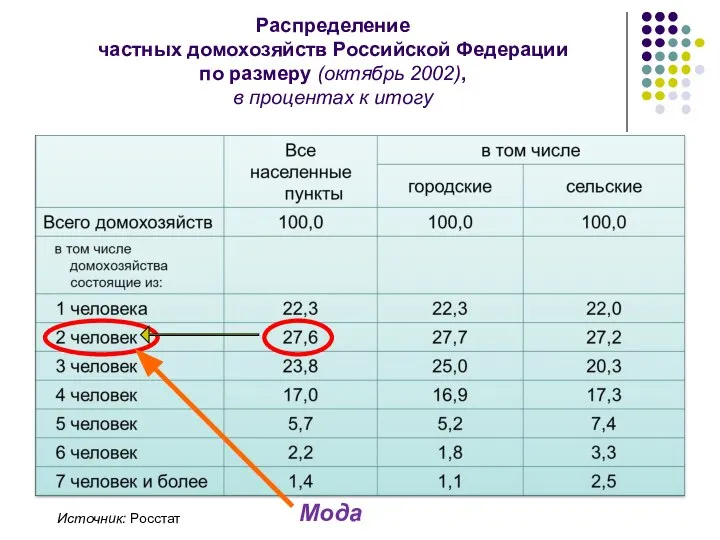
- 45. Распределение частных домохозяйств Российской Федерации по размеру (октябрь 2002), в процентах к итогу Источник: Росстат Мода
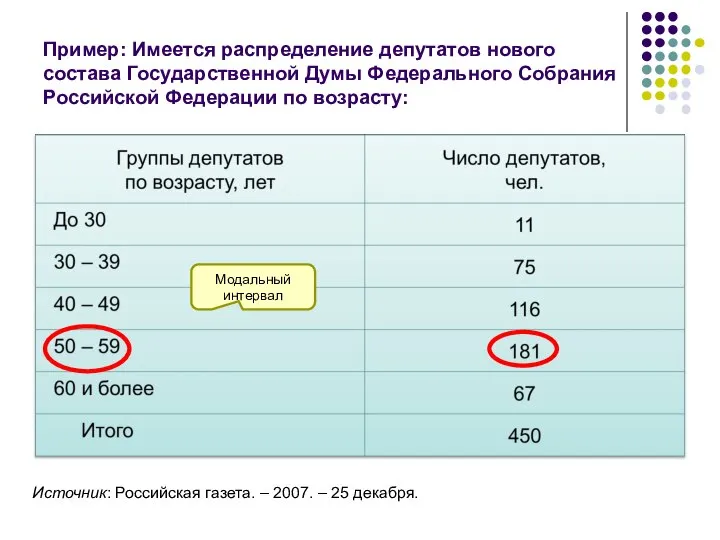
- 46. Пример: Имеется распределение депутатов нового состава Государственной Думы Федерального Собрания Российской Федерации по возрасту: Источник: Российская
- 47. года Условием использования данных алгоритмов является равенство интервалов.
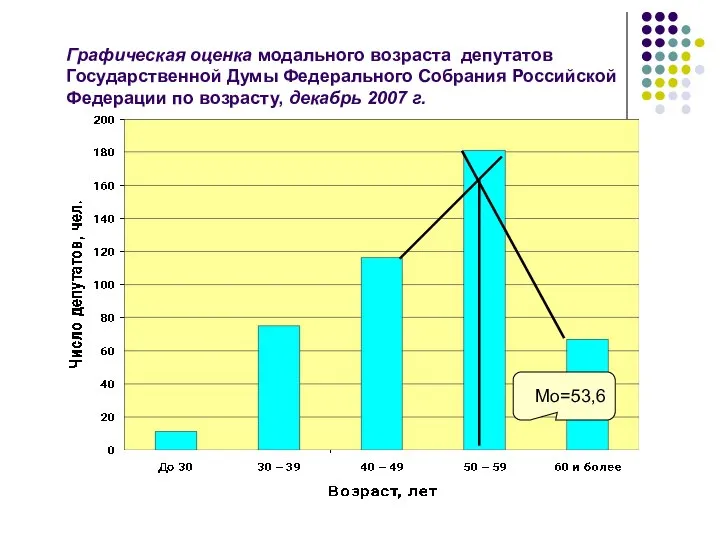
- 48. Графическая оценка модального возраста депутатов Государственной Думы Федерального Собрания Российской Федерации по возрасту, декабрь 2007 г.
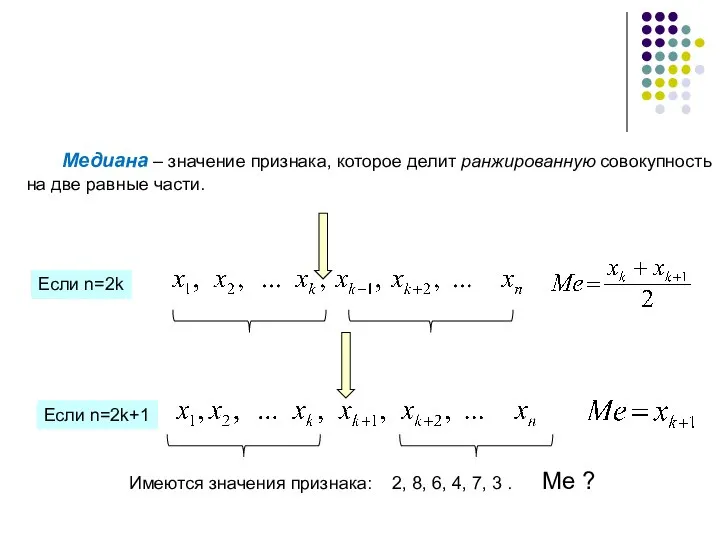
- 49. Медиана – значение признака, которое делит ранжированную совокупность на две равные части. Если n=2k Если n=2k+1
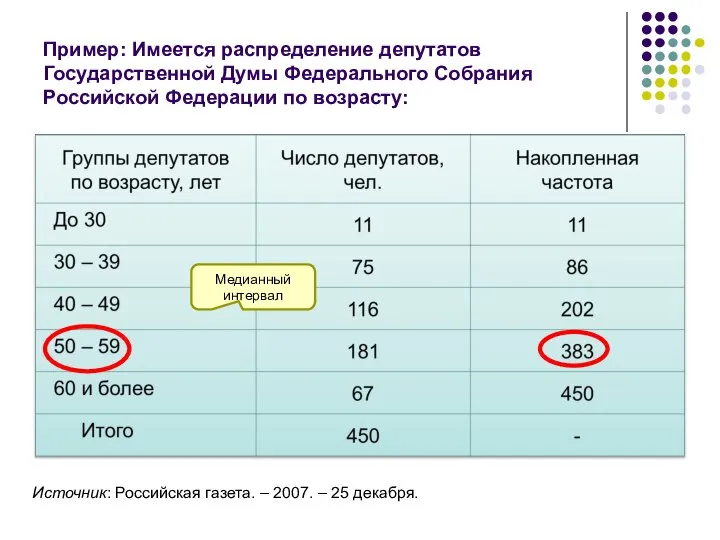
- 50. Пример: Имеется распределение депутатов Государственной Думы Федерального Собрания Российской Федерации по возрасту: Источник: Российская газета. –
- 51. В интервальных вариационных рядах распределения медиана определяется: года
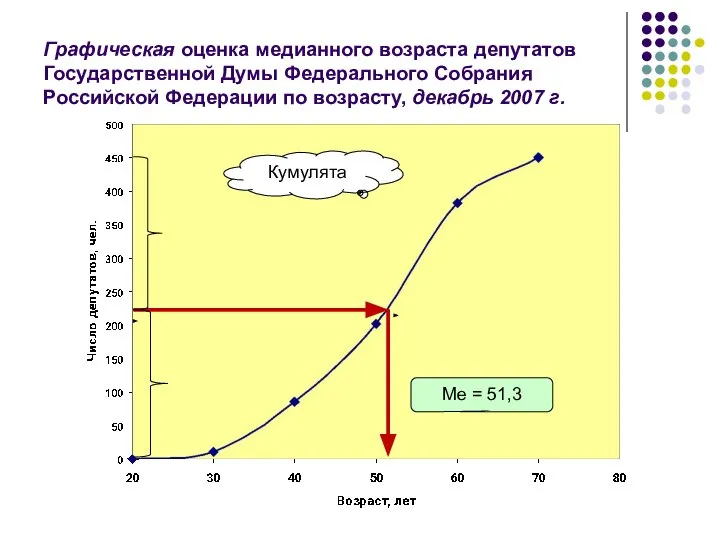
- 52. Графическая оценка медианного возраста депутатов Государственной Думы Федерального Собрания Российской Федерации по возрасту, декабрь 2007 г.
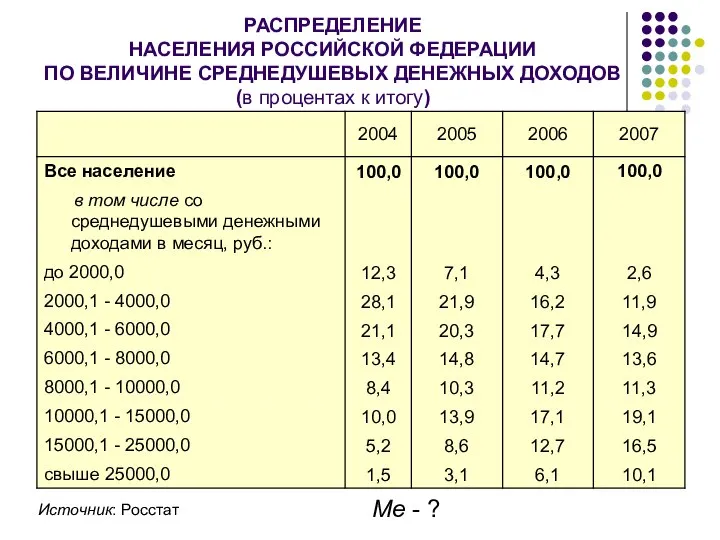
- 53. РАСПРЕДЕЛЕНИЕ НАСЕЛЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ВЕЛИЧИНЕ СРЕДНЕДУШЕВЫХ ДЕНЕЖНЫХ ДОХОДОВ (в процентах к итогу) Источник: Росстат Ме
- 54. руб. руб.
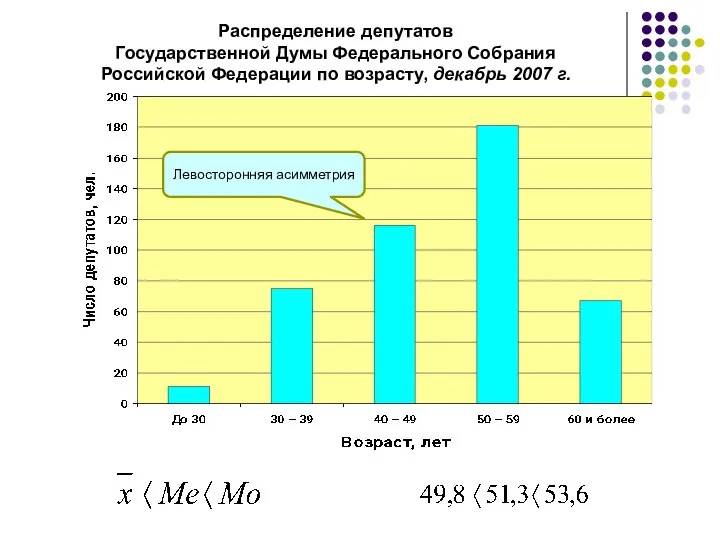
- 55. Между значениями средней арифметической , модой и медианой существует взаимосвязь. Если распределение имеет левостороннюю асимметрию, то
- 56. Левосторонняя асимметрия Распределение депутатов Государственной Думы Федерального Собрания Российской Федерации по возрасту, декабрь 2007 г.
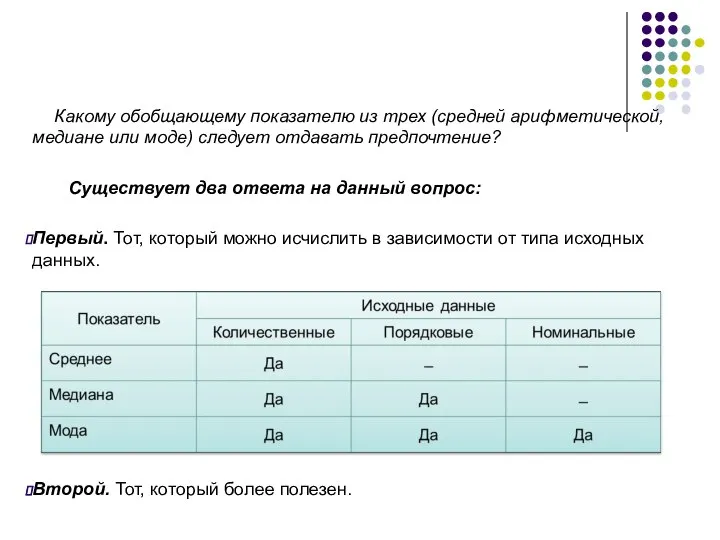
- 57. Какому обобщающему показателю из трех (средней арифметической, медиане или моде) следует отдавать предпочтение? Существует два ответа
- 58. Тесты для контроля знаний Количественное соотношение между двумя частями одной совокупности в статистике выражает относительная величина:
- 60. Скачать презентацию


















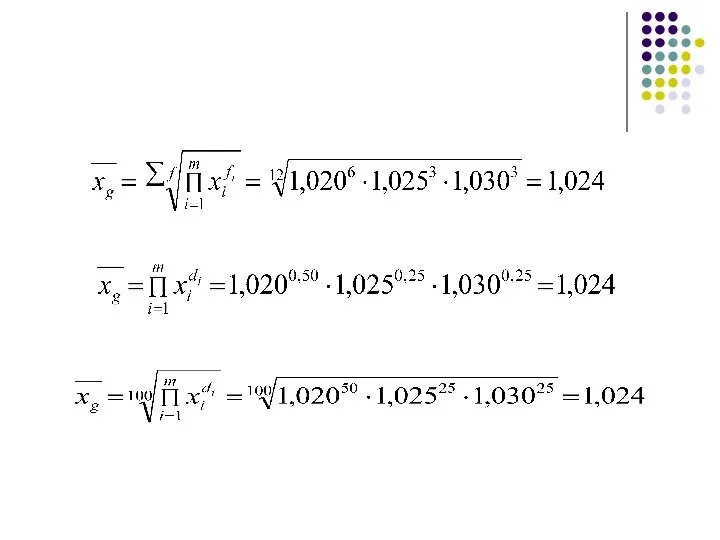






 Решение уравнений. 6 класс
Решение уравнений. 6 класс Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Графики функций у = ах2+n и y= a(x – m)2
Графики функций у = ах2+n и y= a(x – m)2 Многогранники. Призма
Многогранники. Призма Показательная функция
Показательная функция Графы. Способы задания графов. Степени вершин
Графы. Способы задания графов. Степени вершин Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Таблица умножения на 2
Таблица умножения на 2 Правильные многоугольники
Правильные многоугольники Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс Презентация на тему Алгебраические уравнения произвольных степеней 10 класс
Презентация на тему Алгебраические уравнения произвольных степеней 10 класс  Периметр восьмиугольника
Периметр восьмиугольника Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Векторное кодирование графической информации
Векторное кодирование графической информации Окружность
Окружность Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Параллелепипед
Параллелепипед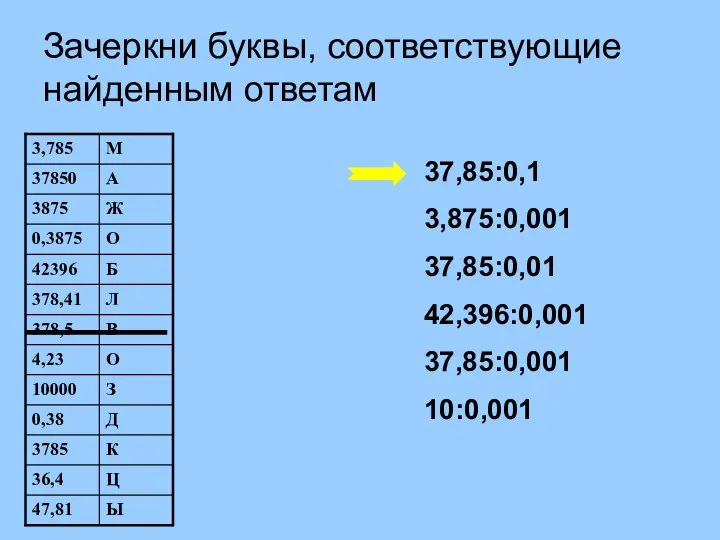 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Элементы нелинейного функционального анализа. Гладкие многообразия
Элементы нелинейного функционального анализа. Гладкие многообразия Моделирование – способ, процесс замещения оригинала его аналогом (моделью)
Моделирование – способ, процесс замещения оригинала его аналогом (моделью) Задачи на проценты
Задачи на проценты Живая планета!
Живая планета! Квадратные уравнения
Квадратные уравнения Устный счет в пределах 10. Состав чисел 7, 8
Устный счет в пределах 10. Состав чисел 7, 8 Моделирование на графах
Моделирование на графах Стороны треугольника пропорциональны синусам противолежащих углов
Стороны треугольника пропорциональны синусам противолежащих углов