Содержание
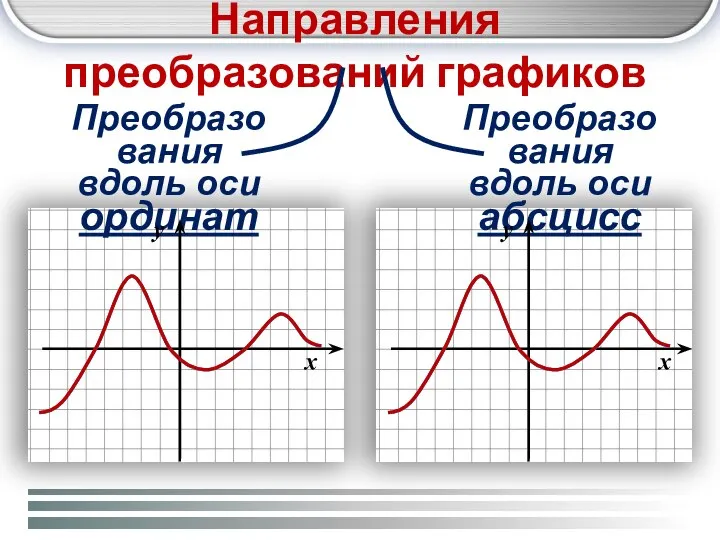
- 2. Направления преобразований графиков Преобразования вдоль оси ординат Преобразования вдоль оси абсцисс x y x y
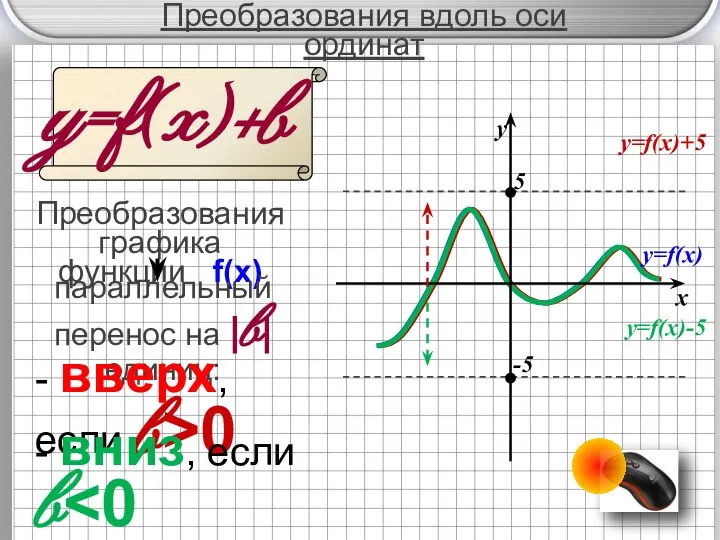
- 3. y=f(x) Преобразования графика функции f(x) +b параллельный перенос на |b| единиц: - вверх, если b>0 -
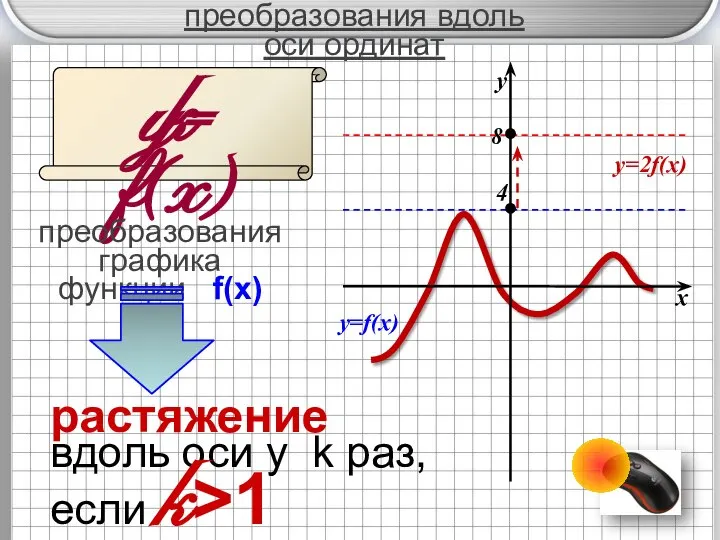
- 4. преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) k растяжение вдоль oси у k
- 5. преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) k x y y=f(x) y=1/2 f(x)
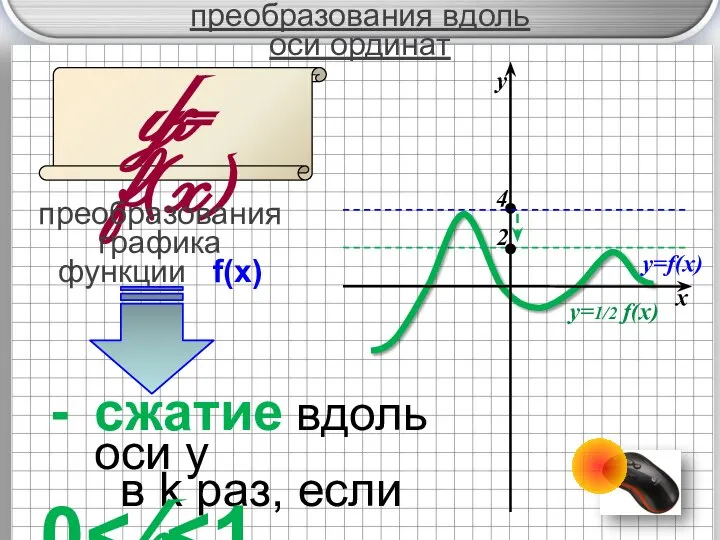
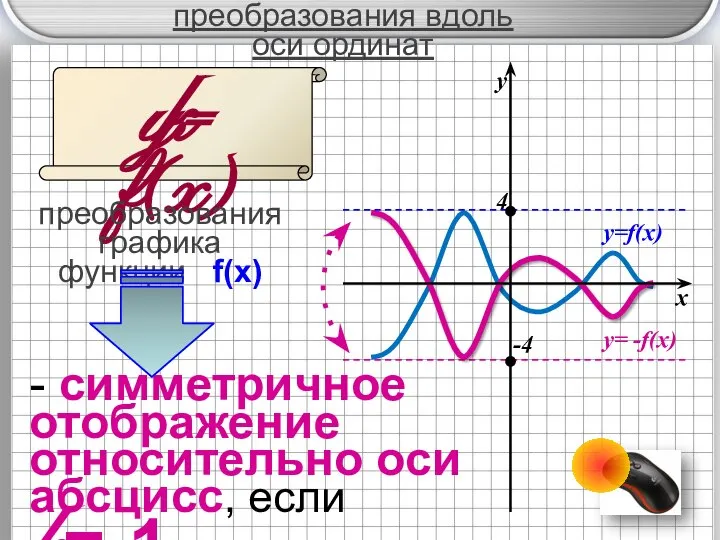
- 6. преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) k - симметричное отображение относительно оси
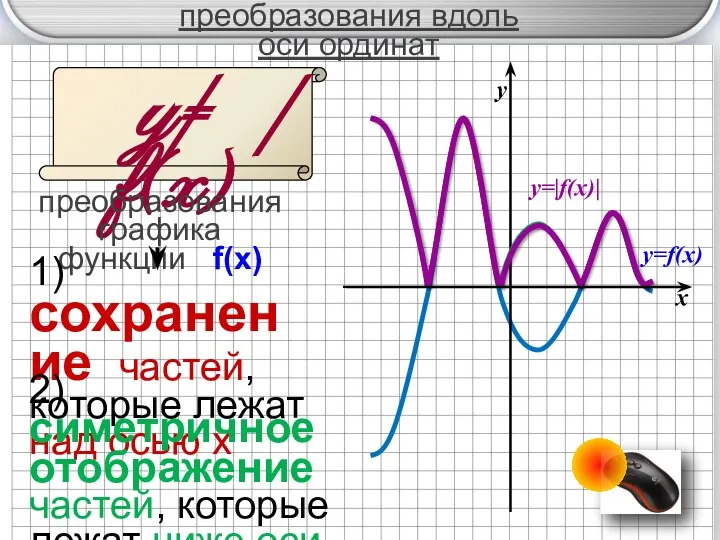
- 7. преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) | | 1) сохранение частей, которые
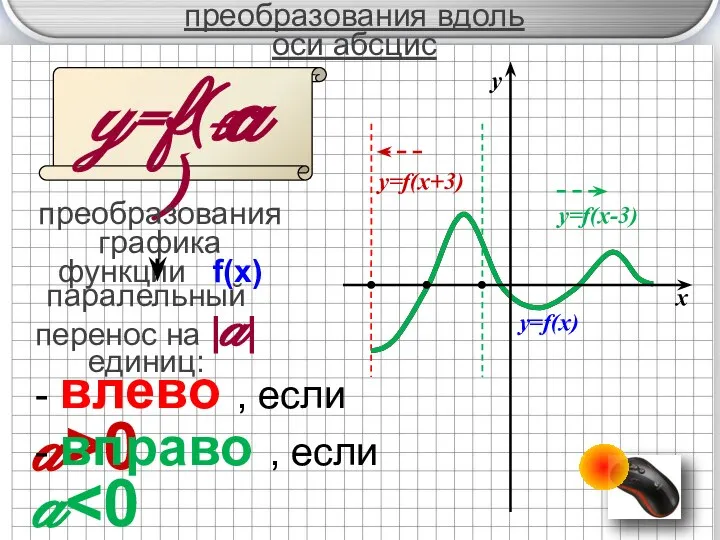
- 8. преобразования вдоль оси абсцис y=f(x ) преобразования графика функции f(x) +a паралельный перенос на |a| единиц:
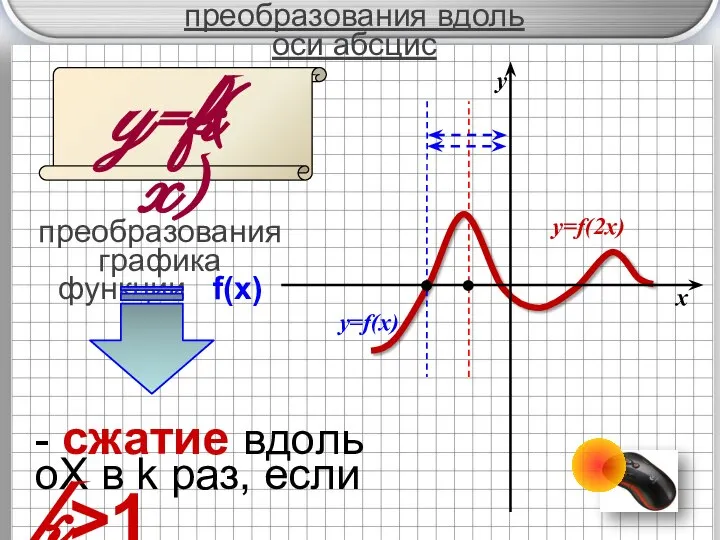
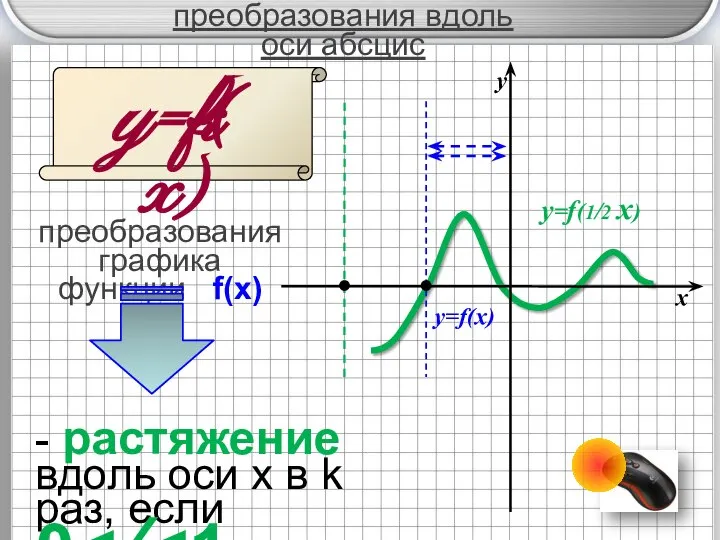
- 9. преобразования вдоль оси абсцис y=f( x) преобразования графика функции f(x) k - сжатие вдоль oX в
- 10. преобразования вдоль оси абсцис y=f( x) преобразования графика функции f(x) k - растяжение вдоль oси х
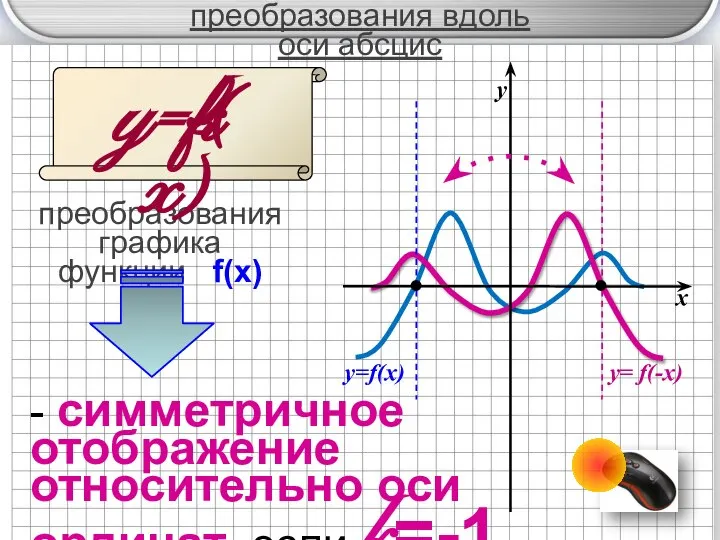
- 11. преобразования графика функции f(x) - симметричное отображение относительно оси ординат, если k=-1 x y y=f(x) y=
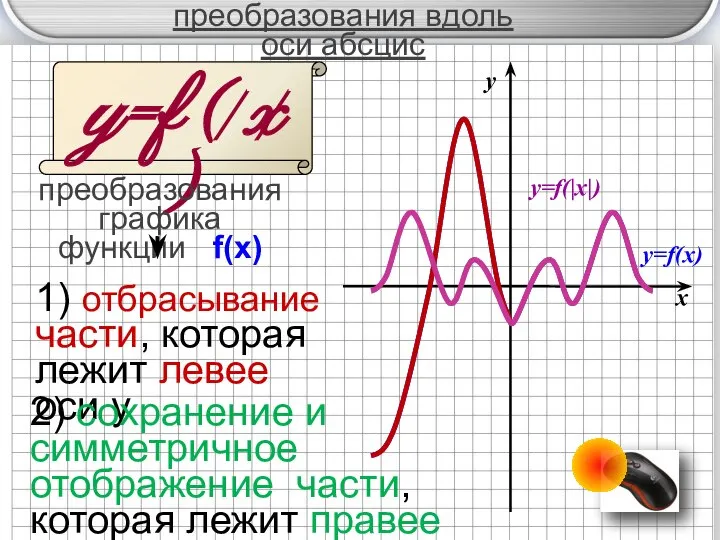
- 12. y=f ( x ) преобразования графика функции f(x) | | 1) отбрасывание части, которая лежит левее
- 13. Примеры построения графиков функций при помощи геометрических преобразований
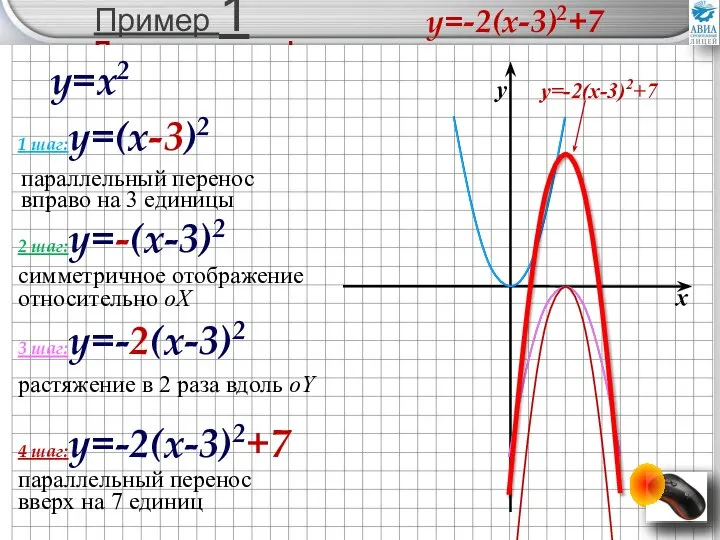
- 14. Пример 1 При помощи геометрических преобразований графика функции y=x2 постройте график функции y=-2(x-3)2+7 1 шаг параллельный
- 15. Пример 1 Построение графика y=x2 1 шаг:y=(x-3)2 2 шаг:y=-(x-3)2 3 шаг:y=-2(x-3)2 4 шаг:y=-2(x-3)2+7 параллельный перенос вправо
- 16. Пример 2 При помощи геометрических преобразований графика функции y=x2 постройте график функции y=|x2-6x+4| Выделим полний квадрат
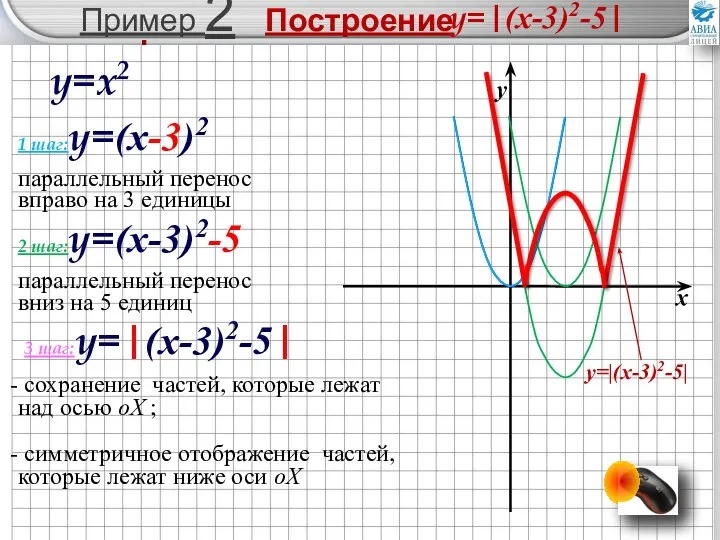
- 17. Пример 2 Построение графика y=x2 1 шаг:y=(x-3)2 2 шаг:y=(x-3)2-5 3 шаг:y=|(x-3)2-5| параллельный перенос вправо на 3
- 18. Пример 3 При помощи геометрических преобразований графика функции y=√x постройте график функции 1 шаг параллельный перенос
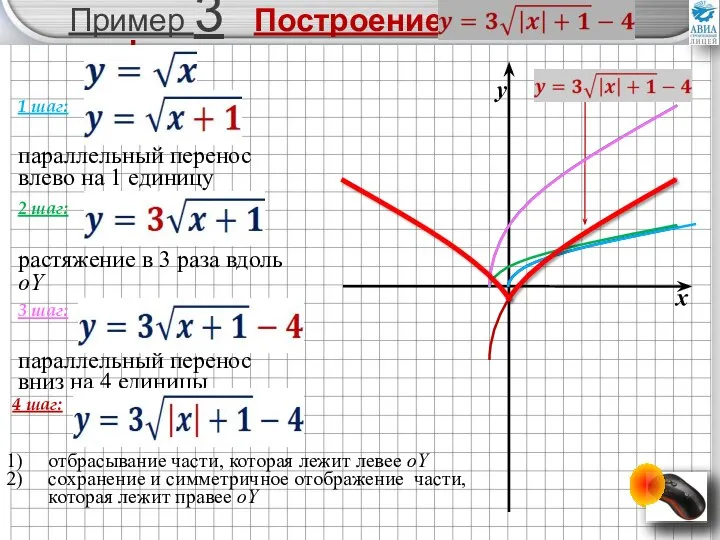
- 19. Пример 3 Построение графика 1 шаг: 2 шаг: 3 шаг: 4 шаг: параллельный перенос влево на
- 20. Отдельные случаи построения графиков при помощи геометрических преобразований +
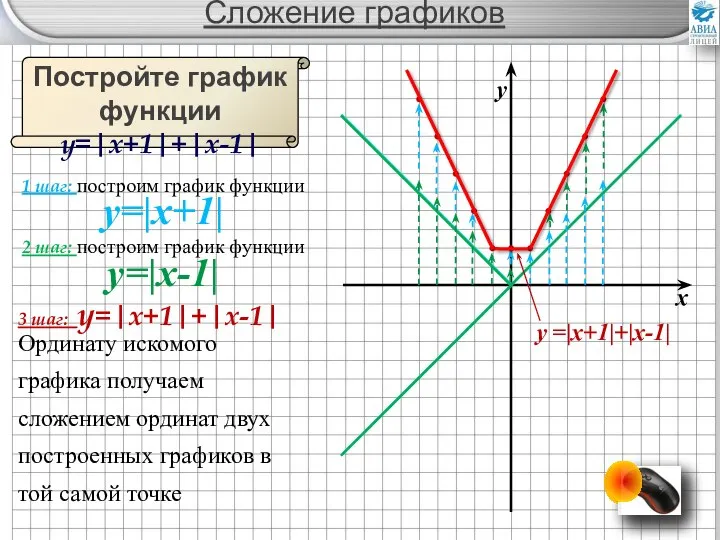
- 21. Сложение графиков Постройте график функции y=|x+1|+|x-1| 1 шаг: построим график функции y=|x+1| 2 шаг: построим график
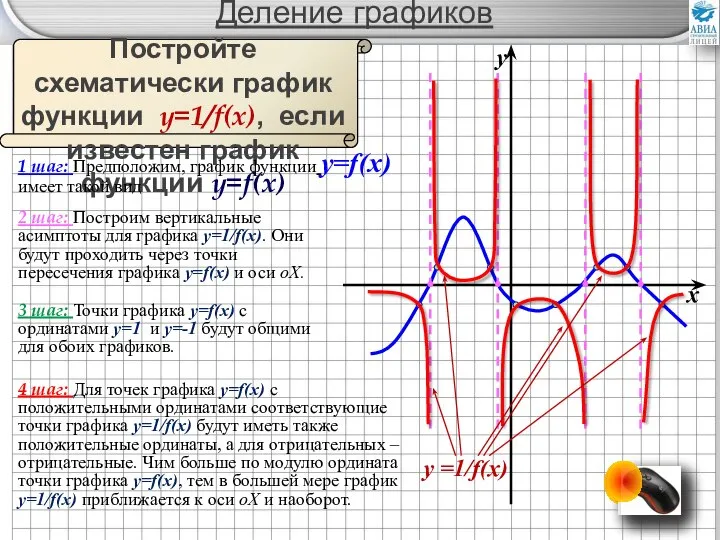
- 22. Деление графиков Постройте схематически график функции y=1/f(x), если известен график функции y=f(x) 1 шаг: Предположим, график
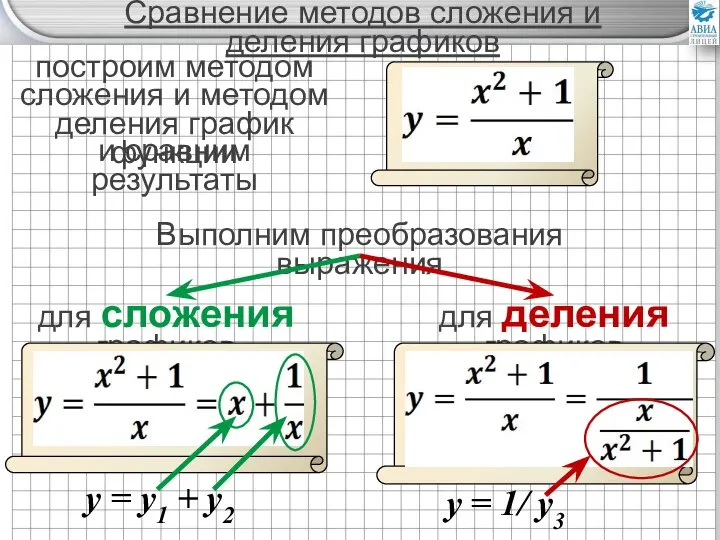
- 23. Сравнение методов сложения и деления графиков построим методом сложения и методом деления график функции и сравним
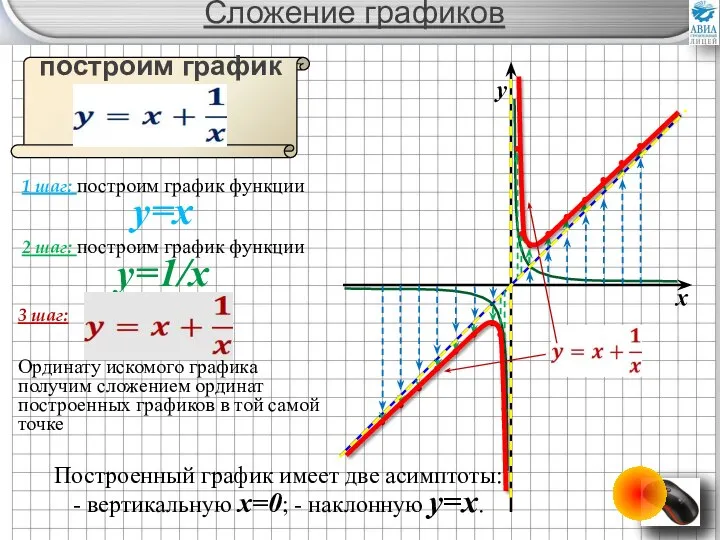
- 24. Сложение графиков построим график функции 1 шаг: построим график функции y=x 2 шаг: построим график функции
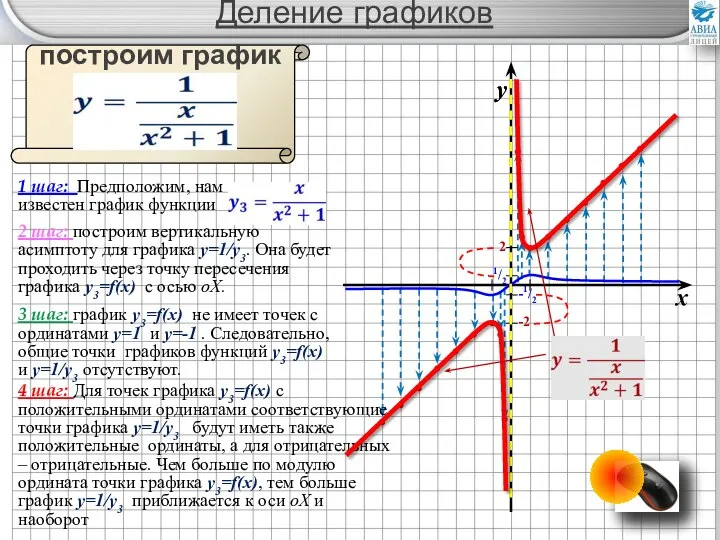
- 25. Деление графиков построим график функции 1 шаг: Предположим, нам известен график функции 2 шаг: построим вертикальную
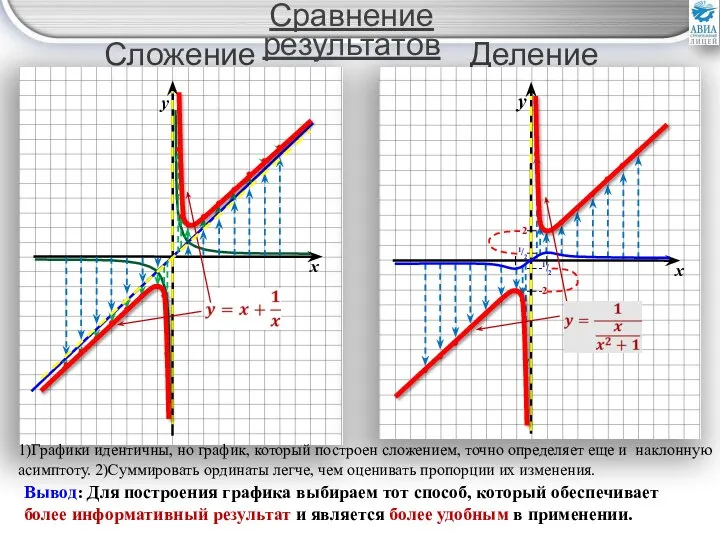
- 26. Сложение графиков Сравнение результатов Деление графиков 1)Графики идентичны, но график, который построен сложением, точно определяет еще
- 27. Успехов в изучении математики!
- 29. Скачать презентацию






 Презентация на тему Число и цифра 9
Презентация на тему Число и цифра 9  Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) Структура арифметической задачи
Структура арифметической задачи Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Геометрия. Решение задач
Геометрия. Решение задач Страна геометрических фигур
Страна геометрических фигур Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Відстань між двома точками. Координати середини відрізка
Відстань між двома точками. Координати середини відрізка Прямая и плоскость
Прямая и плоскость Неравенства с двумя переменными
Неравенства с двумя переменными Функция y = x2 и её график
Функция y = x2 и её график Существование треугольника, равного данному (7 класс)
Существование треугольника, равного данному (7 класс) Смешанные дроби. 5 клас
Смешанные дроби. 5 клас Математика как наука. Матем методы
Математика как наука. Матем методы Признаки делимости
Признаки делимости Графы. Пути с таблицами
Графы. Пути с таблицами Практикум по эконометрике
Практикум по эконометрике Решение задач
Решение задач Построение сечений тетраэдра
Построение сечений тетраэдра Углы в пространстве. Перпендикулярность плоскостей
Углы в пространстве. Перпендикулярность плоскостей Страна Математика
Страна Математика Степени числа
Степени числа Поворот
Поворот Форма вариаций
Форма вариаций Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Числительные. Количественные числительные
Числительные. Количественные числительные Преобразование графиков
Преобразование графиков Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)