Содержание
- 2. Разделы лекции Основные понятия дисперсионного анализа Однофакторный дисперсионный анализ Двухфакторный дисперсионный анализ без повторений Двухфакторный дисперсионный
- 3. 1. Основные понятия дисперсионного анализа Дисперсионный анализ – статистический метод, предназначенный для оценки влияния различных факторов
- 4. Задача дисперсионного анализа – по результатам наблюдений над случайной величиной Y оценить зависимость её математического ожидания
- 5. Модели дисперсионного анализа Два вида факторов: со случайными уровнями и с фиксированными. 1. Модель с фиксированными
- 6. Допущения дисперсионного анализа: случайные ошибки эксперимента имеют нормальный закон распределения с нулевым средним и неизвестной дисперсией;
- 7. 2. Однофакторный дисперсионный анализ Исходные данные для однофакторного анализа
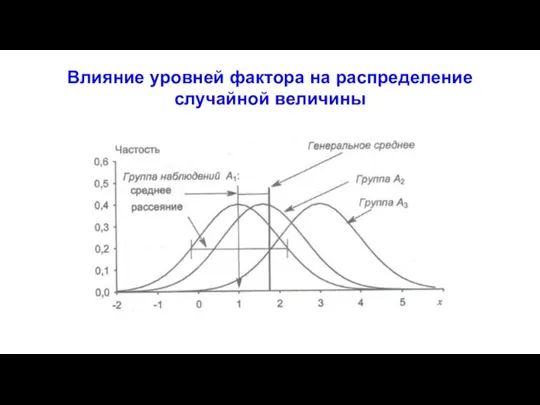
- 8. Влияние уровней фактора на распределение случайной величины
- 9. Математическая модель
- 11. Расчётные формулы
- 14. Схема однофакторного дисперсионного анализа
- 15. Проверка гипотезы в однофакторном дисперсионном анализе
- 16. Пример 1 Исследовалось влияние трёх видов катализаторов А1, А2, А3 на выход целевого продукта (в т).
- 17. Решение примера 1
- 19. Оценки дисперсий:
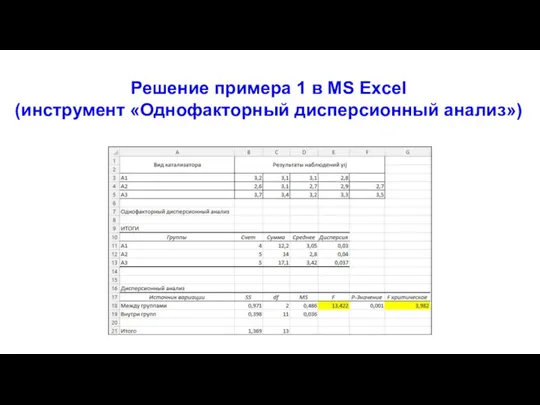
- 20. Решение примера 1 в MS Excel (инструмент «Однофакторный дисперсионный анализ»)
- 21. Линейные контрасты
- 23. Пример 2
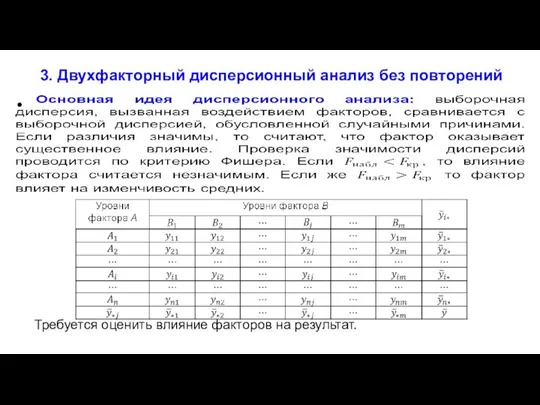
- 24. 3. Двухфакторный дисперсионный анализ без повторений Требуется оценить влияние факторов на результат.
- 25. Математическая модель
- 26. Схема двухфакторного дисперсионного анализа без повторений
- 27. Гипотезы в двухфакторном дисперсионном анализе без повторений
- 28. Проверка гипотез в двухфакторном дисперсионном анализе без повторений
- 29. Пример 3
- 30. Решение примера 3
- 31. Решение примера 3 (продолжение)
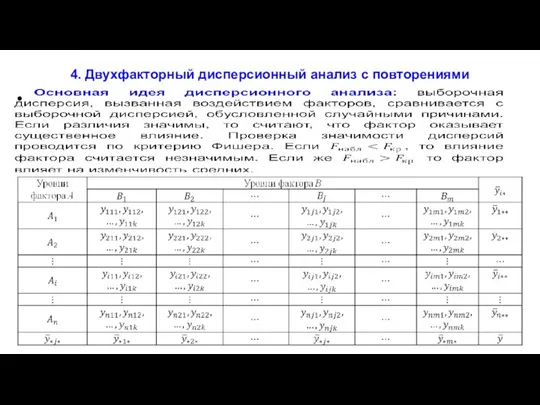
- 32. 4. Двухфакторный дисперсионный анализ с повторениями
- 33. Математическая модель
- 34. Схема двухфакторного дисперсионного анализа с повторениями
- 35. Гипотезы в двухфакторном дисперсионном анализе с повторениями
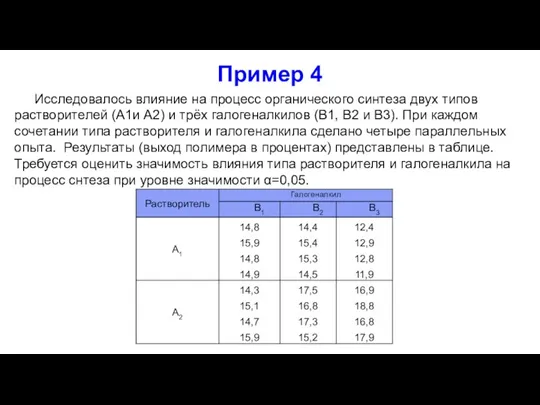
- 36. Пример 4 Исследовалось влияние на процесс органического синтеза двух типов растворителей (A1и A2) и трёх галогеналкилов
- 37. Решение примера 4
- 38. Решение примера 4 (продолжение)
- 39. 5. Однофакторный анализ Краскела-Уоллиса
- 40. Вычисление критерия Краскела-Уоллиса при наличии связанных рангов
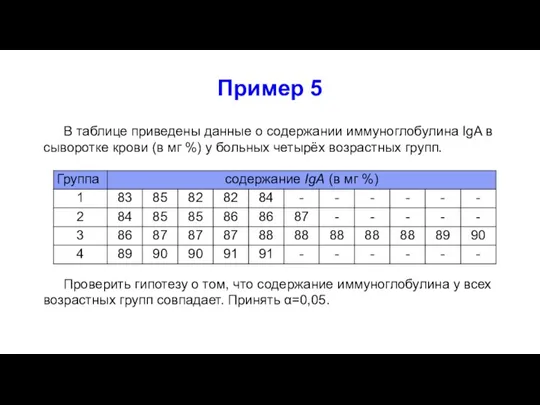
- 41. Пример 5 В таблице приведены данные о содержании иммуноглобулина IgA в сыворотке крови (в мг %)
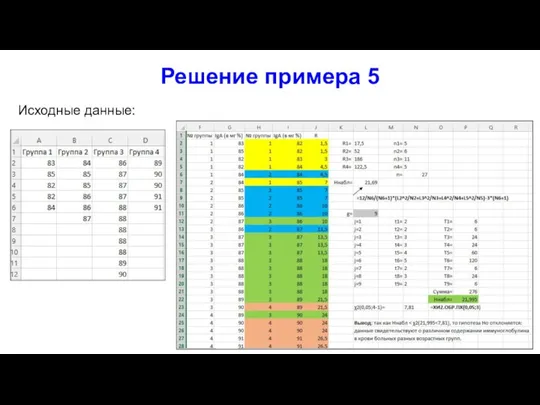
- 42. Решение примера 5 Исходные данные:
- 43. 6. Двухфакторный анализ Фридмана
- 44. Коэффициент конкордации Кендалла
- 45. Пример 6 Киноплёнка четырёх видов была представлена трём экспертам для определения лучшей из них. Каждому эксперту
- 46. Решение примера
- 47. Заключение Рассмотрены основные понятия дисперсионного анализа. Приведены расчетные формулы для проведения однофакторного и двухфакторного дисперсионного анализа,
- 48. Литература Вадзинский Р. Статистические вычисления в среде Excel. Библиотека пользователя. – СПб. : Питер, 2008. –
- 50. Скачать презентацию








































 Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -  Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Старинные меры длины
Старинные меры длины Статистическая проверка гипотез
Статистическая проверка гипотез Сбережение водных ресурсов. Решение задач на сравнение величин
Сбережение водных ресурсов. Решение задач на сравнение величин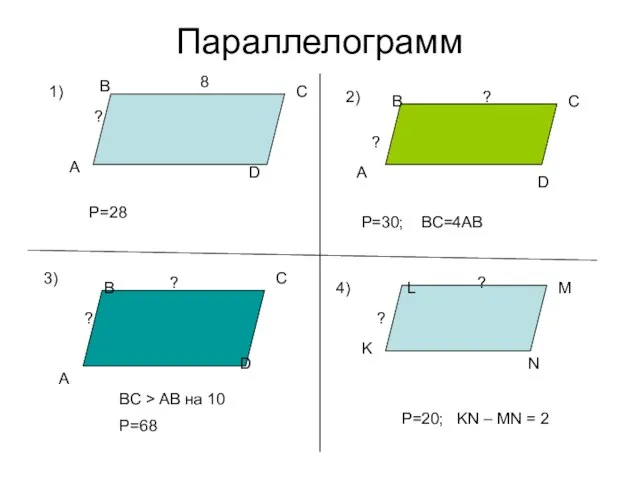 Параллелограмм
Параллелограмм Окружность Аполлония
Окружность Аполлония Формирование и развитие познавательных УУД на уроках математики
Формирование и развитие познавательных УУД на уроках математики Интерактивный плакат Треугольник
Интерактивный плакат Треугольник Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями
Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями Тест по теме Окружность
Тест по теме Окружность Презентация на тему Показательная функция: свойства, график
Презентация на тему Показательная функция: свойства, график  Интерактивный пазл
Интерактивный пазл Маршрутный лист группы
Маршрутный лист группы Credit and exam
Credit and exam Квадратные уравнения. Лекция
Квадратные уравнения. Лекция Система быстрого счёта в уме Якова Трахтенберга. Занятия 3
Система быстрого счёта в уме Якова Трахтенберга. Занятия 3 Скалярное произведение векторов
Скалярное произведение векторов Рациональные и действительные числа. Приближенные выражения
Рациональные и действительные числа. Приближенные выражения Планиметрия. Задачи
Планиметрия. Задачи Задача на внимание. 5 класс
Задача на внимание. 5 класс 3.7. Непрерывность функции
3.7. Непрерывность функции Четырехугольники
Четырехугольники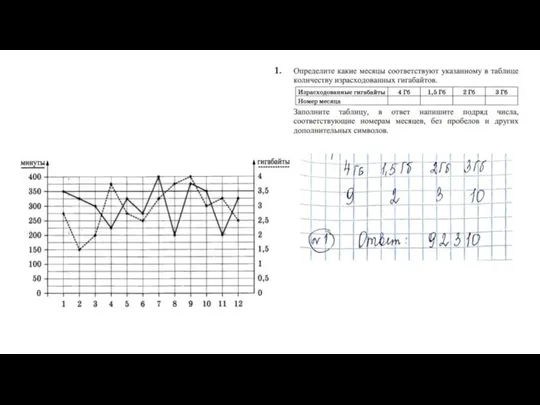 Решение задач
Решение задач Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация на тему Функция у=к/х, её свойства и график
Презентация на тему Функция у=к/х, её свойства и график  Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Рисуем по координатам
Рисуем по координатам