Слайд 2Предмет комбинаторики
Комбинаторика – это раздел математики, который изучает задачи выбора и расположения

элементов из некоторого множества в соответствии с заданными правилами.
Типичные задачи комбинаторики:
«Сколькими способами можно сделать … ?», «Сколько вариантов существует … ?», «Сколькими способами можно выбрать столько-то объектов?» и т.п.
Слайд 3Предмет комбинаторики
Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности

случайных событий и, соответственно, получения законов распределения случайных величин.
Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для понимания статистических закономерностей.
Слайд 4Правила комбинаторики
1. Правило суммы
Если некоторые k действий взаимно исключают друг друга, причем

первое действие можно выполнить n1 способами, второе – n2 способами, третье – n3 способами и т.д. до k-го действия, которое можно выполнить nk способами, то выполнить одно любое из этих действий можно числом способов, равным:
Слайд 5Правила комбинаторики
2. Правило произведения
Пусть требуется выполнить последовательно k действий. Если первое действие

можно выполнить n1 способами, второе действие – n2 способами, третье – n3 способами и т.д. до k-го действия, которое можно выполнить nk способами, то все k действий могут вместе быть выполнены числом способов, равным:
Слайд 6Факториал
Факториал – операция произведения всех натуральных чисел от единицы до заданного n

включительно:
Например:
По определению:
Слайд 7Свойства факториала
Отношение двух факториалов упрощается следующим образом:

Слайд 8Перестановки без повторений
Число перестановок определяет, сколькими способами можно переставить n элементов множества.
Если

элементы множества можно считать различными, то применяется формула подсчета числа перестановок без повторений:
Слайд 9Перестановки с повторениями
Если в рассматриваемом множестве присутствуют одинаковые элементы, причем элементов первого

типа n1 штук, элементов второго – n2 штук, третьего – n3 и т.д. до k-го типа элементов, общее число которых равно nk, то применяется формула подсчета числа перестановок с повторениями:
Слайд 10Сочетания без повторений
Число сочетаний определяет, сколькими способами можно выбрать m элементов из

множества, состоящего из n элементов.
Если элементы множества можно считать различными, то применяется формула подсчета числа сочетаний без повторений:
Слайд 11Сочетания с повторениями
Если в множестве присутствуют одинаковые элементы, причем число различных типов

элементов равно n, и из них требуется выбрать m элементов (причем все m элементов могут быть одного типа), то применяется формула подсчета числа сочетаний с повторениями:
Слайд 12Размещения без повторений
Число размещений определяет, сколькими способами можно выбрать m элементов из

множества, состоящего из n элементов, и в каждой выборке переставить их местами.
Если элементы множества можно считать различными, то применяется формула подсчета числа размещений без повторений:
Слайд 13Размещения с повторениями
Если каждый из n элементов множества можно выбирать неоднократно, то

применяется формула подсчета числа размещений с повторениями:












 ЛекцияЭлементы комбинаторики
ЛекцияЭлементы комбинаторики Основы метрологии
Основы метрологии Сумма углов треугольника
Сумма углов треугольника Определение функций. Построение и чтение графиков функций
Определение функций. Построение и чтение графиков функций Перпендикулярні площини. Практика 1
Перпендикулярні площини. Практика 1 Решение тригонометрических уравнений
Решение тригонометрических уравнений Сложение дробей с один знаменателем
Сложение дробей с один знаменателем Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь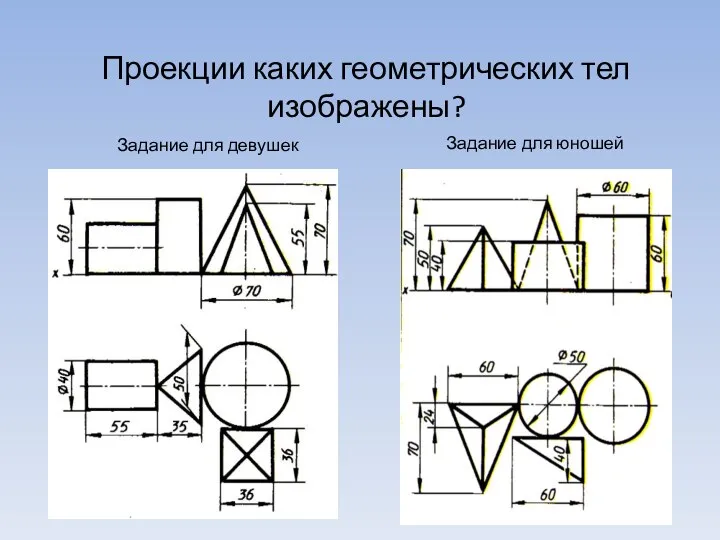 Проекции каких геометрических тел изображены?
Проекции каких геометрических тел изображены? Элементы математической логики
Элементы математической логики Сложение чисел
Сложение чисел Криволинейные интегралы. Теория поля
Криволинейные интегралы. Теория поля Элементы теории обобщенных функций
Элементы теории обобщенных функций Математика. Билет 5
Математика. Билет 5 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Случайные величины
Случайные величины Методы кластеризации
Методы кластеризации Начала теории вероятностей
Начала теории вероятностей Решение задач
Решение задач Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата Путешествие в историю математики. Решение старинных задач
Путешествие в историю математики. Решение старинных задач Икосаэдр
Икосаэдр Презентация на тему Приёмы устного решения квадратного уравнения
Презентация на тему Приёмы устного решения квадратного уравнения  Скорость сближения и скорость удаления
Скорость сближения и скорость удаления Презентация на тему Такая разная геометрия
Презентация на тему Такая разная геометрия  Изображение пространственных фигур
Изображение пространственных фигур Числовые промежутки
Числовые промежутки Диагонали прямоугольника
Диагонали прямоугольника