Основы математической статистики в метрологии. Часть 2

*
Основные законы распределения вероятностей непрерывной случайной величины
Равномерный закон распределения

*
Задание
Выведите формулы для вычисления дисперсии и математического ожидания равномерного закона распределения.
Для этого используйте определение этих характеристик.

*
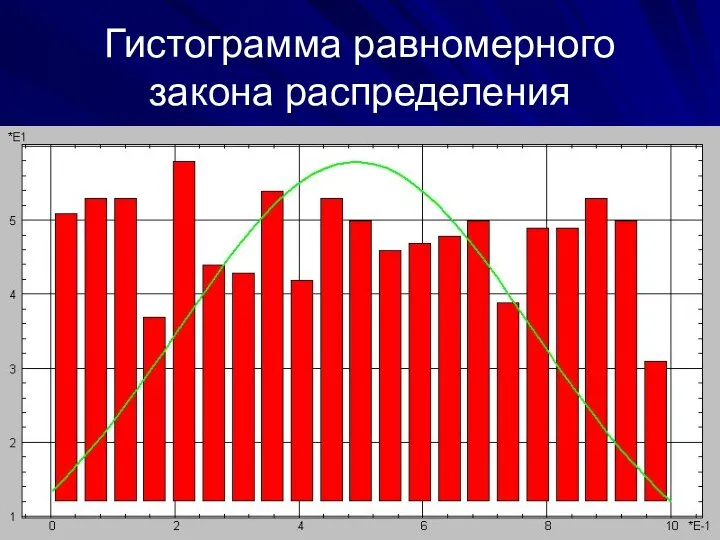
Гистограмма равномерного закона распределения

*
Примеры равномерного закона распределения
Погрешности прямых измерений
Погрешность округления.
Случайная составляющая погрешности дискретного прибора при незначительном разбросе измерений (1-3 дискрета)

*
Пример из ГОСТ 8.207
Оценку суммарного СКО результата измерения вычисляют

*
Нормальный закон распределения
N(mx,σx)

*
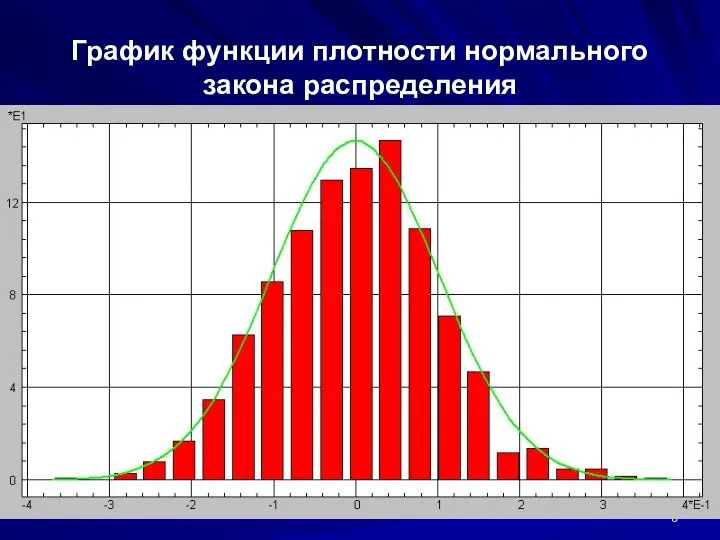
График функции плотности нормального закона распределения

*
Нормированная случайная величина
Задание:
Доказать, что для нормированной случайной величины
M(u) = 0 σ2(u) = 1

*
Вопрос
Пусть три случайные величины X,Y,Z имеют нормальное распределение с известными математическими ожиданиями и дисперсиями (предположим, имеются три измерительных канала температуры): M(X)=50, D(X)=0,3 , M(Y)=70, D(Y)=0,5, M(Z)=90, D(Z)=0,7
Постройте функции плотности распределения f(x), f(y), f(z).
Постройте для них нормированные функции плотности распределения.

*
Распределение χ2
Пусть Z1, Z2 ... Zν независимые нормированные случайные величины N(0, 1).
M(Z)=0, D(Z)=1
- есть хи-квадрат (χ2 ) распределение с параметром ν. Этот параметр называется числом степеней свободы.

*
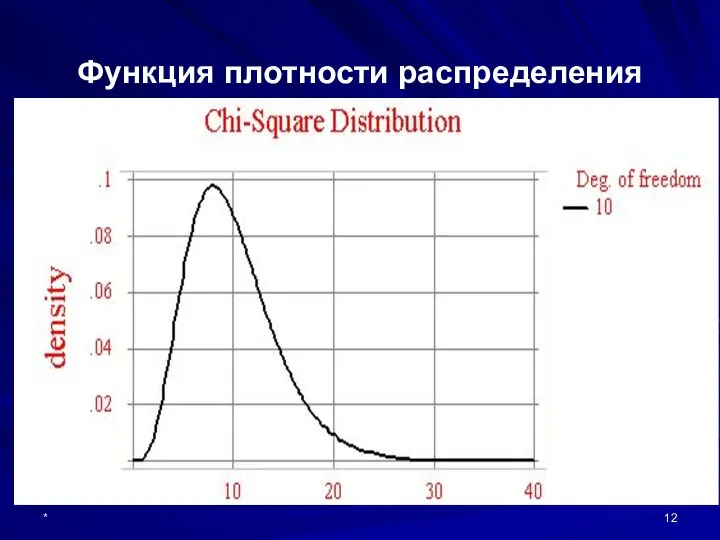
Функция плотности распределения

*
Пример распределения χ2
Оценка дисперсии по выборке
В дальнейшем будем использовать эту статистику

*
Распределение Стъюдента
Z → N(0,1), V → χ2(ν)
Z,V – независимые
M(t)=0 D(t)= ν/ν-2
случайная величина t (t-статистика) ,
- распределение Стъюдента

*
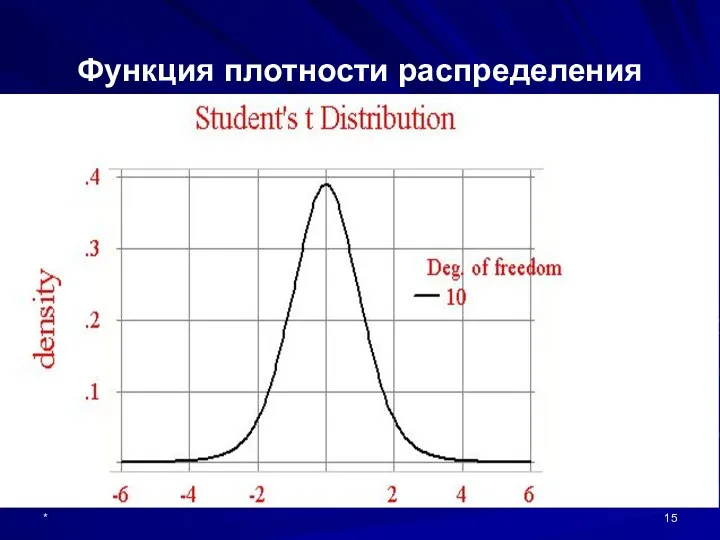
Функция плотности распределения

*
Пример
В чем отличие и
Вопрос :
Приведите примеры использования распределения Стъюдента в Ваших практических задачах.

*
Распределение Фишера
Если U, V – независимые случайные величины,
U – имеет χ2(ν1) с ν1 степенями свободы,
V - имеет χ2(ν2) с ν2 степенями свободы
имеет распределение Фишера
с ν1 и ν2 степенями свободы

*
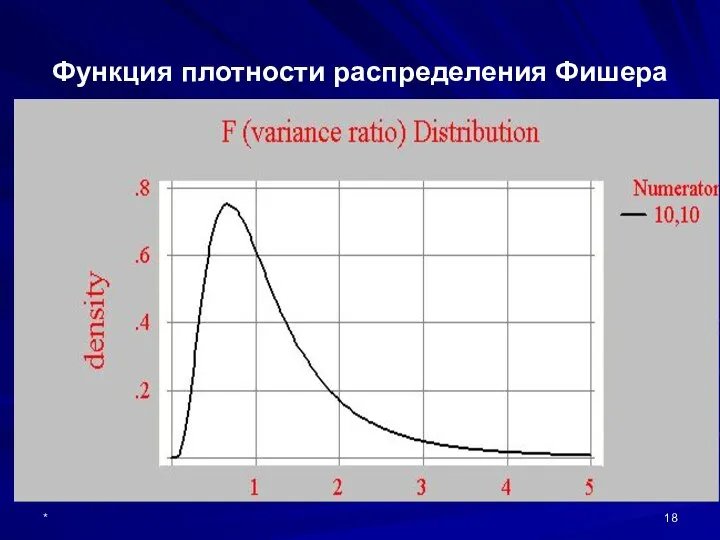
Функция плотности распределения Фишера

*
Пример
Проверяется гипотеза о равенстве дисперсий двух выборок
X: x1, x2, ..., xn
Y: y1, y2, ..., ym
Отношение двух выборочных нормированных дисперсий есть распределение Фишера с n-1 и m-1 степенями свободы.
Вопрос: Приведите примеры использования распределения Фишера в Ваших практических задачах.

*
Что такое выборка?
Выборкой называют последовательность независимых одинаково распределенных случайных величин.
ξ - случайная величина
x1, x2, …, xn – выборка

*
Показатели описательной статистики
Показатели положения (относительно среднего)
среднее арифметическое
среднее геометрическое
медиана P(x ≤ M) = P(x ≥ M) = 1/2
мода - положение max

*
Показатели рассеяния
Дисперсия
Стандартное отклонение
Размах xmax – xmin
Межквартальный размах – 50% выборки

*
Показатели формы
Асимметрия
Эксцесс
Моменты

*
Квантиль
Квантилью уровня α (или α – квантилью) непрерывной случайной величины ξ , имеющей непрерывную функцию распределения F(x), называется значение Xα для которого
P (ξ< Xα) = α
Часто встречающиеся в практике квантили.
Медиана - квантиль, соответствующая значению α =0,5
Верхняя квартиль – квантиль, соответствующий значению α =0,75
Нижняя квартиль – квантиль, соответствующий значению
α =0,25
Децили – квантили уровней 0,1; 0,2; ... , 0,9.

*
Квантиль Xα случайной величины, имеющей функцию распределения F(x)
F(x)
F(xp)
xp
x

*
Примеры решения прямой задачи в EXCEL
Для нормального закона распределения,
=НОРМСТРАСП(1.96) = 0.975002
=НОРМСТРАСП(-1.96) = 0.024998
Для распределения Стъюдента
=СТЬЮДРАСП(1.96;100;1) = 0.026389
=СТЬЮДРАСП(1.96;200;1) = 0.025692
1.96 – заданное значение X,
100,200 – число степеней свободы,
1 - односторонний интервал

*
Примеры решения обратной задачи в EXCEL
Для нормального закона распределения по заданной вероятности найдем квантиль
=НОРМСТОБР(0.025) = -1.96
=НОРМСТОБР(0.975) = 1.96
Решение обратной задачи для распределения Стъюдента
=СТЬЮДРАСПОБР(0.05;500) = 1.96472 Соответствует Р= 0.975
=СТЬЮДРАСПОБР(0.01;500) = 2.585698 Соответствует Р= 0.995

*
Спасибо
за
Внимание !!!