Содержание
- 2. Особливими випадками є: − наявність альтернативного оптимуму; − виродженість розв’язку; − необмеженість цільової функції; − відсутність
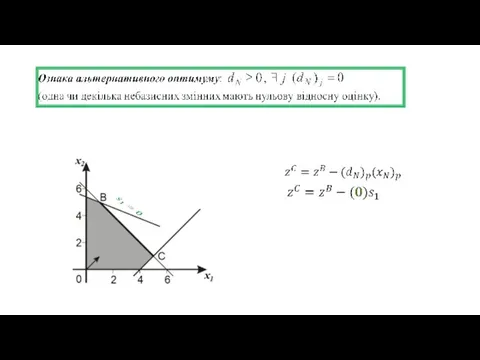
- 3. Альтернативний оптимум
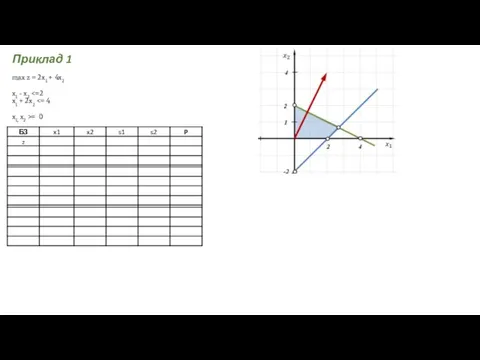
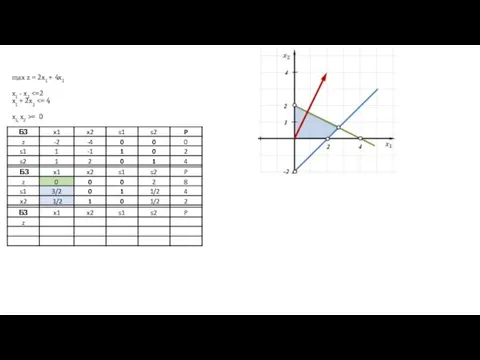
- 5. max z = 2x1 + 4x2 x1 - x2 = 0 Приклад 1
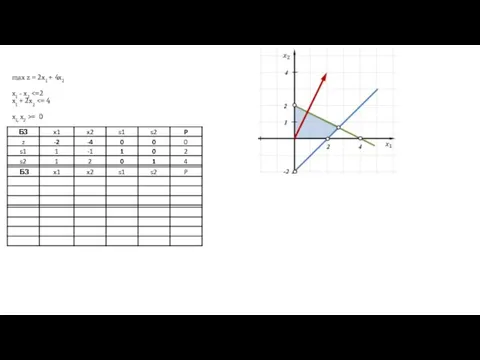
- 6. max z = 2x1 + 4x2 x1 - x2 = 0
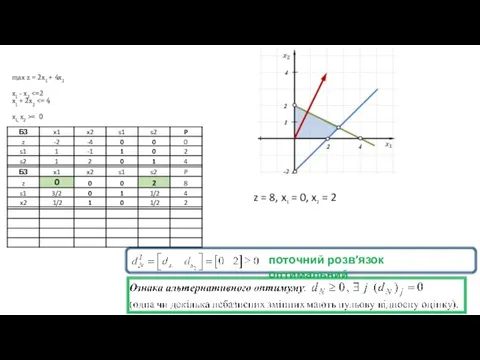
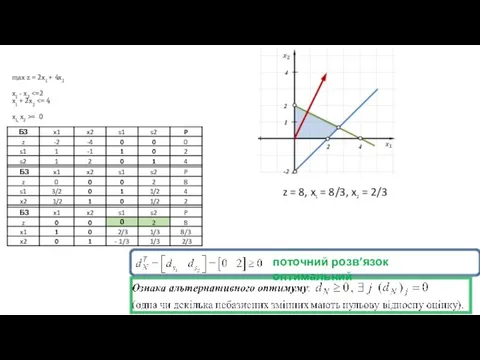
- 7. max z = 2x1 + 4x2 x1 - x2 = 0 z = 8, x1 =
- 8. max z = 2x1 + 4x2 x1 - x2 = 0
- 9. max z = 2x1 + 4x2 x1 - x2 = 0 z = 8, x1 =
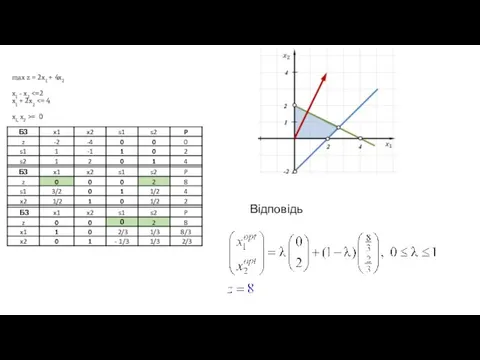
- 10. max z = 2x1 + 4x2 x1 - x2 = 0 Відповідь
- 11. Альтернативний оптимум Можливі три випадки: 1) альтернативний оптимум –(нескінчена) обмежена множина; 2) альтернативний оптимум – (нескінчена)
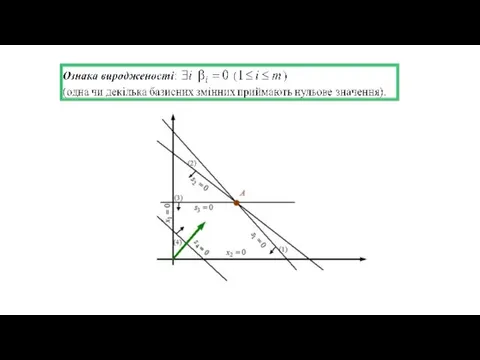
- 12. Виродженість
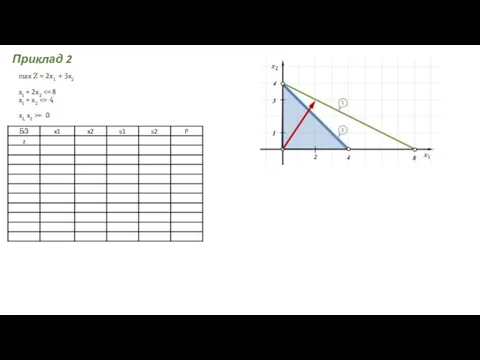
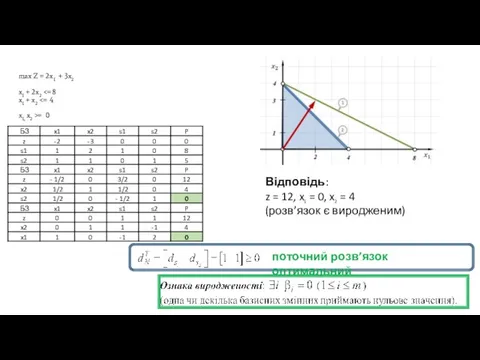
- 14. max Z = 2x1 + 3x2 x1 + 2x2 = 0 Приклад 2
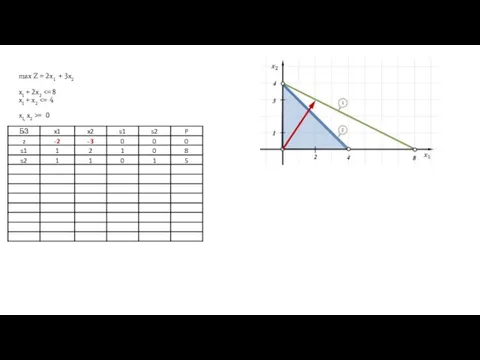
- 15. max Z = 2x1 + 3x2 x1 + 2x2 = 0
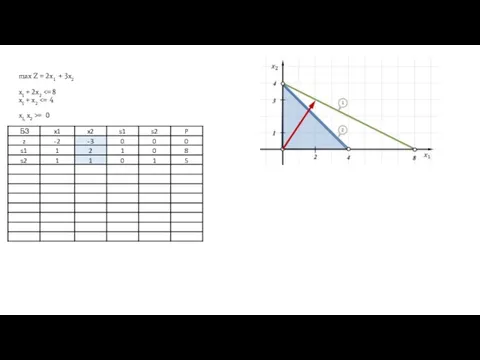
- 16. max Z = 2x1 + 3x2 x1 + 2x2 = 0
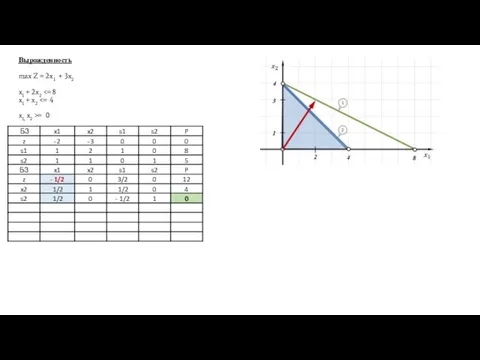
- 17. Вырожденность max Z = 2x1 + 3x2 x1 + 2x2 = 0
- 18. max Z = 2x1 + 3x2 x1 + 2x2 = 0 Відповідь: z = 12, x1
- 19. Необмеженість ЦФ
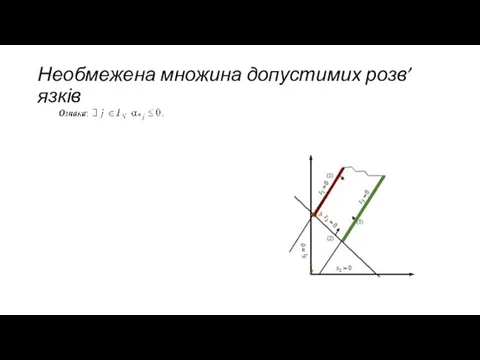
- 20. Необмежена множина допустимих розв’язків
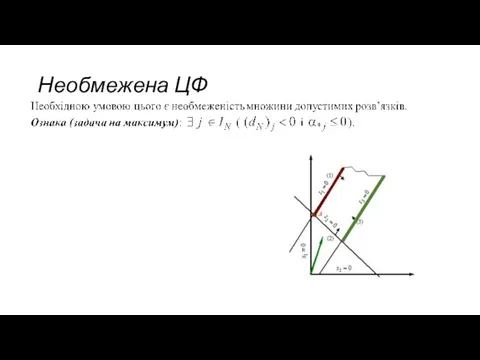
- 21. Необмежена ЦФ
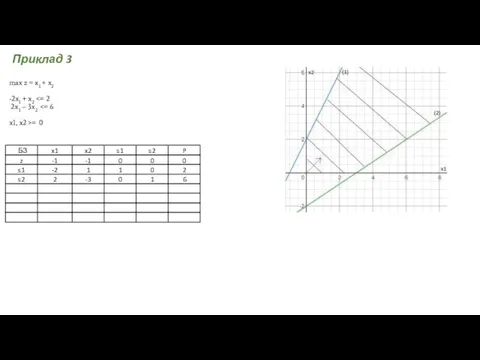
- 22. max z = x1 + x2 -2x1 + x2 = 0 Приклад 3
- 23. max z = x1 + x2 -2x1 + x2 = 0 Відповідь: Задача не має розв’язку,
- 24. Альтернативний оптимум –необмежена множина
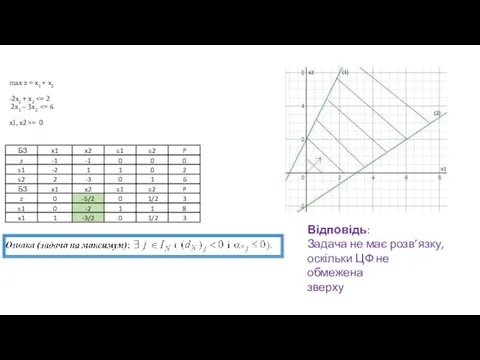
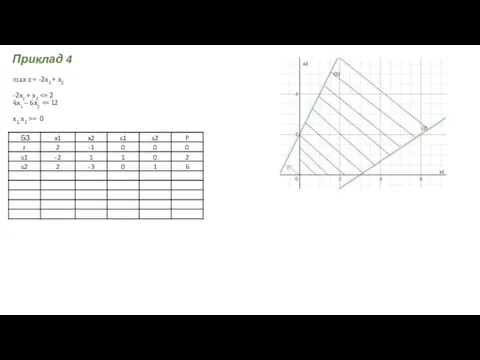
- 25. max z = -2x1 + x2 -2x1 + x2 = 0 Відповідь Приклад 4
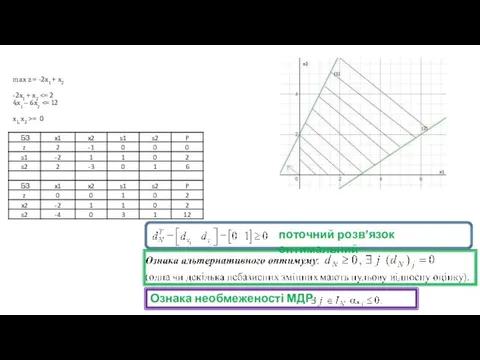
- 26. max z = -2x1 + x2 -2x1 + x2 = 0 Відповідь
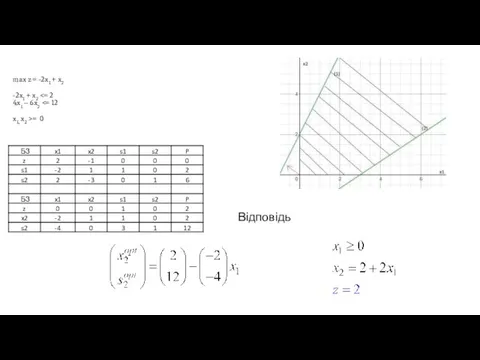
- 27. max z = -2x1 + x2 -2x1 + x2 = 0 Відповідь Відповідь
- 28. Приклади 5 - 9
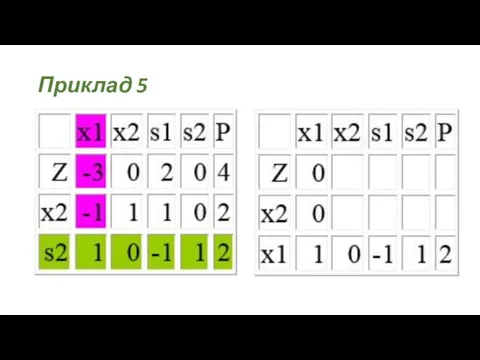
- 29. Приклад 5
- 30. Приклад 5
- 31. Приклад 5 (ДБР1)
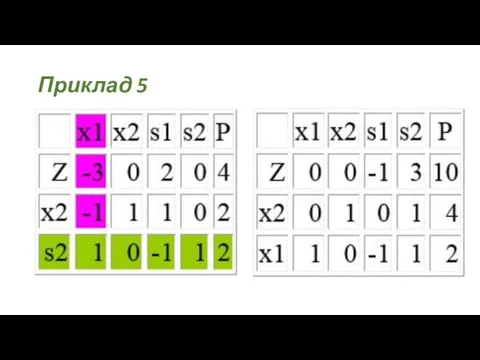
- 32. Приклад 5
- 33. Приклад 5
- 34. Приклад 5
- 35. Приклад 5
- 36. Приклад 5
- 37. Приклад 5
- 38. Приклад 5 (ДБР2)
- 39. Приклад 5
- 40. Приклад 5
- 41. Приклад 5
- 42. Приклад 5
- 43. Приклад 5
- 44. Приклад 5
- 45. Приклад 5 (ДБР3)
- 46. Приклад 5
- 47. Приклад 5 Відповідь: Задача не має розв’язку, оскільки ЦФ не обмежена зверху
- 48. Приклад 5 Усі виконані ітерації СМ можна було не робити, оскільки вже для першого ДБР виконувалась
- 49. Приклад 6
- 50. Приклад 6
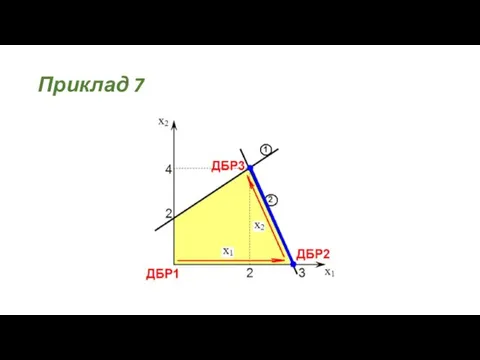
- 51. Приклад 7
- 52. Приклад 7
- 53. Приклад 7 Відповідь:
- 54. Приклад 7
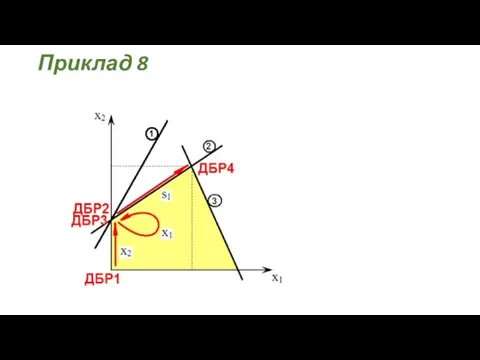
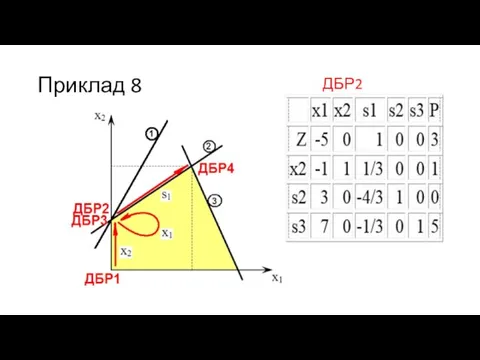
- 55. Приклад 8
- 56. Приклад 8
- 57. Приклад 8
- 58. Приклад 8 ДБР2
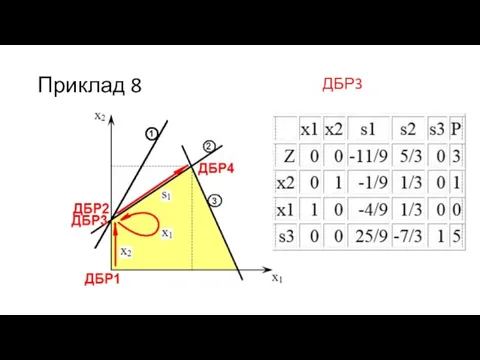
- 59. Приклад 8 ДБР3
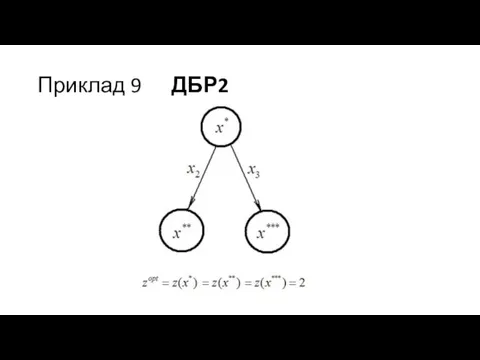
- 60. Приклад 9 (три оптимальні вершини)
- 61. Приклад 9
- 62. Приклад 9
- 63. Приклад 9 ДБР2
- 64. Приклад 9 ДБР2
- 65. Приклад 9
- 66. Приклад 9
- 67. Відсутність допустимих розв’язків
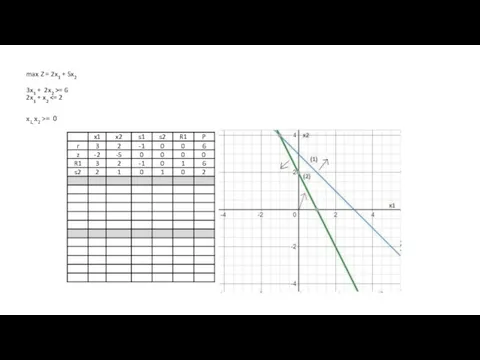
- 68. max Z = 2x1 + 5x2 3x1 + 2x2 >= 6 2x1 + x2 x1, x2
- 69. max Z = 2x1 + 5x2 3x1 + 2x2 >= 6 2x1 + x2 x1, x2
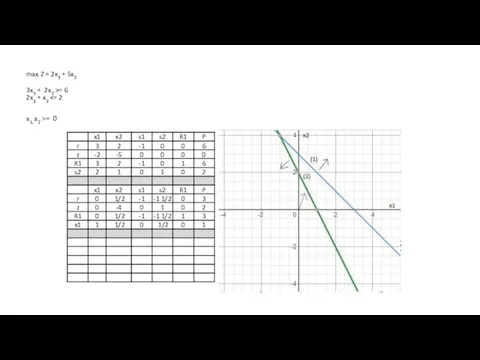
- 70. max Z = 2x1 + 5x2 3x1 + 2x2 >= 6 2x1 + x2 x1, x2
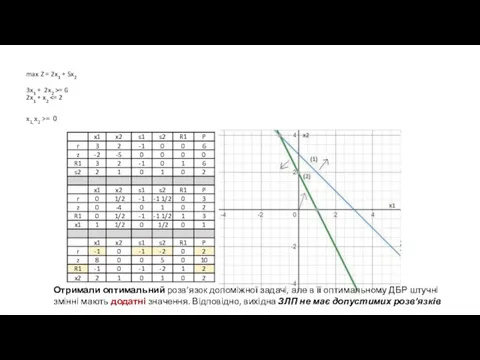
- 71. max Z = 2x1 + 5x2 3x1 + 2x2 >= 6 2x1 + x2 x1, x2
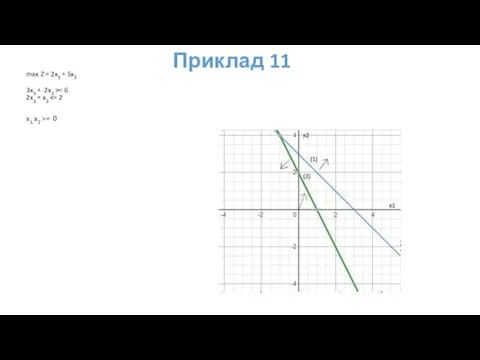
- 72. Приклад 12
- 74. Скачать презентацию








































 Презентация на тему ОБЪЁМ ТЕЛ
Презентация на тему ОБЪЁМ ТЕЛ  Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Решение уравнений: рациональных и иррациональных
Решение уравнений: рациональных и иррациональных Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Это страшное слово: Параметр
Это страшное слово: Параметр Математика и живопись
Математика и живопись Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Тела вращения
Тела вращения Математический кроссворд
Математический кроссворд Графический метод решения уравнений. Задания для устного счета
Графический метод решения уравнений. Задания для устного счета Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Проецирование
Проецирование Тригонометрические функции двойного угла
Тригонометрические функции двойного угла Распределительное свойство умножения
Распределительное свойство умножения Геометрические фигуры
Геометрические фигуры Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Математика, Устный счёт
Математика, Устный счёт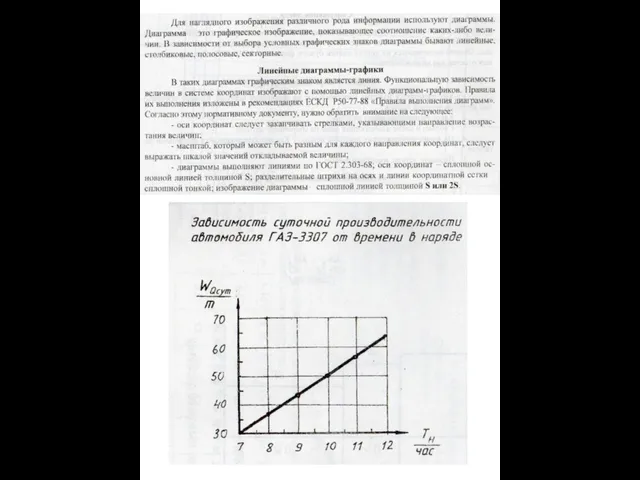 Графики и диаграммы
Графики и диаграммы Единицы измерения, масштабы шкал
Единицы измерения, масштабы шкал Некоторые методические приемы для работы с детьми ЗПР на уроках математики
Некоторые методические приемы для работы с детьми ЗПР на уроках математики Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности
Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Концентрация. Часть II
Концентрация. Часть II Отрицательные числа в географии
Отрицательные числа в географии