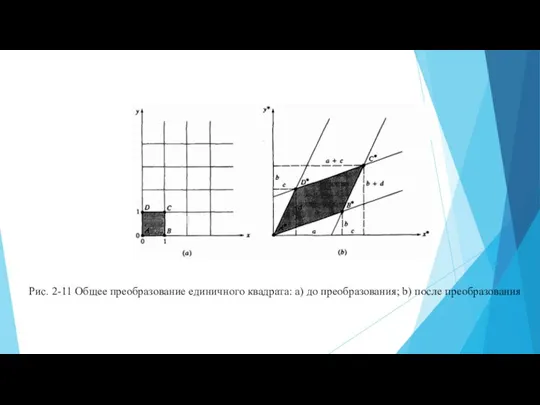
начало координат не подвергается преобразованию, т.е. . Далее отметим, что координаты равны первой строке матрицы преобразования, а координаты - второй. Таким образом, матрица преобразования является определенной, если определены координаты и (преобразование единичных векторов , ). Поскольку стороны единичного квадрата первоначально параллельны и ранее было показано, что параллельные линии преобразуются снова в параллельные, то результирующая фигура является параллелограммом.
Влияние элементов , , и матрицы может быть установлено отдельно. Элементы и , как видно из рис. 2-11b, вызывают сдвиг (см. разд. 2-4) исходного квадрата в направлениях и соответственно. Как отмечалось ранее, элементы и играют роль масштабных множителей. Таким образом, -матрица задает комбинацию сдвига и масштабирования.
Несложно определить также площадь параллелограмма из рис. 2-11b, которую можно вычислить следующим образом:








 Тема: Письменное умножение на двузначное число. Закрепление.
Тема: Письменное умножение на двузначное число. Закрепление. Дроби. 5 класс
Дроби. 5 класс Не ошибись! 56 = 78= 34= 60+4 80+6 90+3 30+60 10+40 50+20 77-7 48-8 26-6 50-40 60-20 80-10
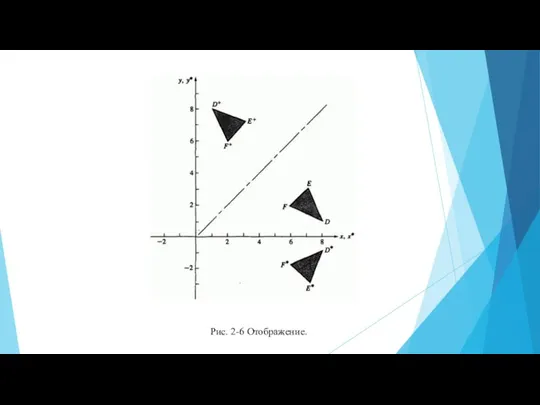
Не ошибись! 56 = 78= 34= 60+4 80+6 90+3 30+60 10+40 50+20 77-7 48-8 26-6 50-40 60-20 80-10 Задача 3. Построить матрицу поворота
Задача 3. Построить матрицу поворота Игра Музыкальная математика
Игра Музыкальная математика Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями
Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями Сумма_и_разность_дробей_с_одинаковыми_знаменателями
Сумма_и_разность_дробей_с_одинаковыми_знаменателями Системы линейных уравнений
Системы линейных уравнений Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Волшебная страна - Геометрия
Волшебная страна - Геометрия Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Математика. Зачем она нам в жизни
Математика. Зачем она нам в жизни Тригонометрические неравенства Слайды для урока по теме:
Тригонометрические неравенства Слайды для урока по теме: Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Статистическое изучение динамики общественных явлений. Лекция №8
Статистическое изучение динамики общественных явлений. Лекция №8 Организация поточного обучения по математике в МАОУ СОШ МАСТЕРГРАД
Организация поточного обучения по математике в МАОУ СОШ МАСТЕРГРАД Множества и операции над ними
Множества и операции над ними Формулы производной тангенса и котангенса
Формулы производной тангенса и котангенса 131024062328
131024062328 Занимательная математика (3 класс)
Занимательная математика (3 класс) Презентация на тему Признаки равенства и подобия треугольников
Презентация на тему Признаки равенства и подобия треугольников  mypresentation.ru
mypresentation.ru Статистические сравнения
Статистические сравнения Построение графиков функций при помощи геометрических преобразований
Построение графиков функций при помощи геометрических преобразований Квадратные уравнения
Квадратные уравнения Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Витамин В6: его формы, участие в рекакциях переаминирования и декарбоксилирования
Витамин В6: его формы, участие в рекакциях переаминирования и декарбоксилирования Учимся считать. Интерактивный тренажёр
Учимся считать. Интерактивный тренажёр