Площадь многоугольника

Задача №1
1. Через точку во внутренней области равностороннего треугольника проведены две прямые, параллельные двум сторонам треугольника. На какие фигуры разбивается этими прямыми данный треугольник?

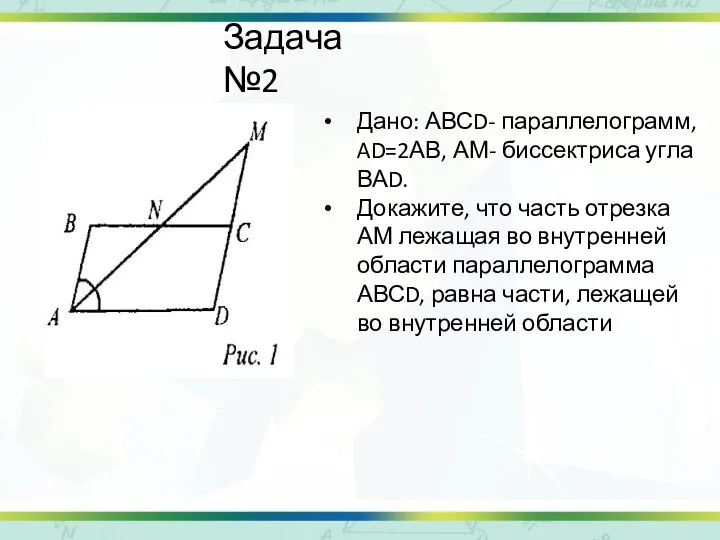
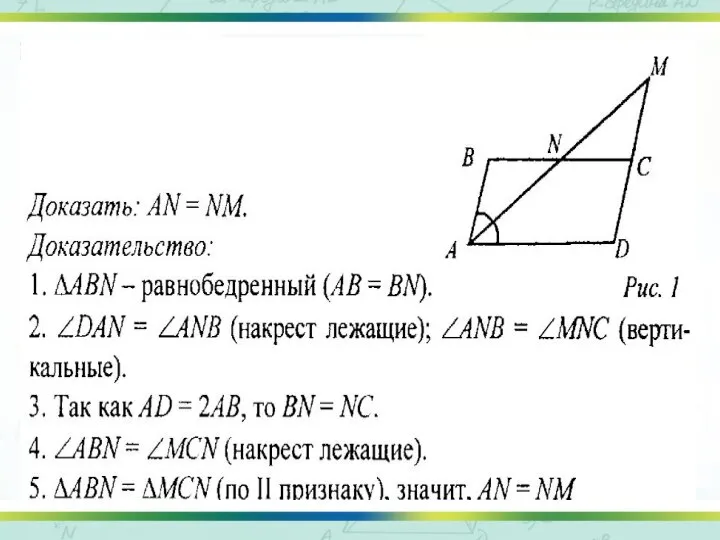
Задача №2
Дано: АВСD- параллелограмм, AD=2АВ, АМ- биссектриса угла ВАD.
Докажите, что часть отрезка АМ лежащая во внутренней области параллелограмма АВСD, равна части, лежащей во внутренней области

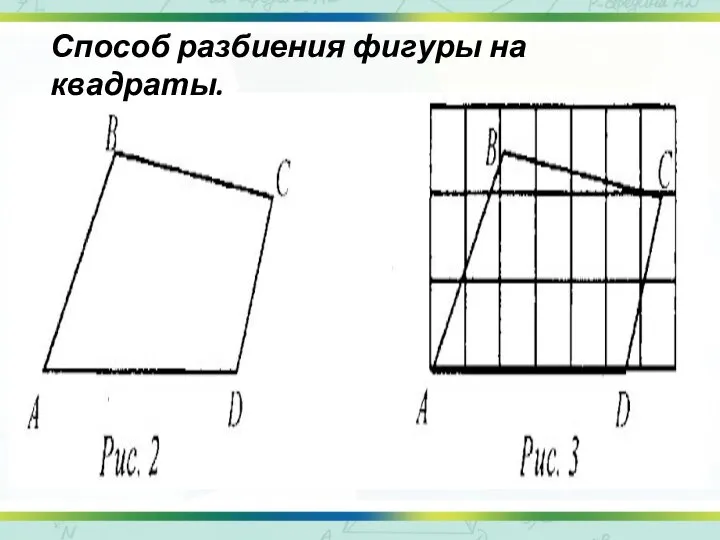
Способ разбиения фигуры на квадраты.

Свойства площадей.
Равные многоугольники имеют равные площади
Если многоугольник составлен из нескольких многоугольников,
то его площадь равна сумме площадей этих многоугольников
3. Площадь квадрата равна квадрату его сторон

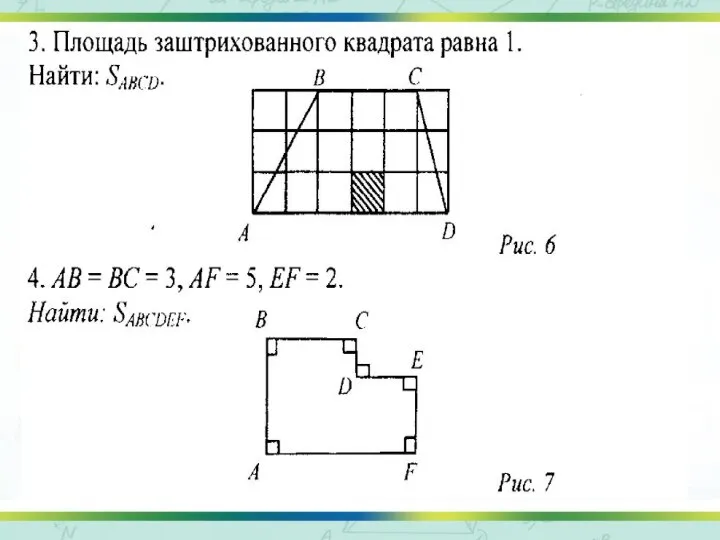
№ 449(в)
а= 3√2 м,
Sкв= а2
Sкв= (3√2) 2 =9*2=18 (м 2)
№ 450 (в)
а= √ Sкв
Sкв= 12 м2
а= √12= √4*3=2 √3(м)
Sкв
а

Самостоятельная работа

Проверка
№449(а)
а= 1,2 см,
Sкв= а2
Sкв= (1,2) 2 =1,44 (см 2)
№450(а)
а= √ Sкв
Sкв= 16 см2
а= √16= 4 (см)
№451
Sкв= 24 см2
а)Sкв= 24 см2 =24*100мм2 =2400мм2
1см2 =100мм2
б) Sкв= 24 см2 =24*0,01дм2 =0.24дм2
1см2 =0,01дм2

Рефлексия
Составьте синквейн к уроку.
Что нового узнали на уроке?