Содержание
- 2. Математическая статистика Задачи математической статистики: 1) определение способов сбора статистических данных, 2) разработка методов анализа статистических
- 3. Выборочный метод Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака. 1) Сплошное
- 4. Выборочный метод Генеральная совокупность – совокупность объектов, из которой производится отбор. Выборочная совокупность (выборка) - совокупность
- 5. Оценки параметров распределения Задача: нахождение оценок параметров распределения случайной величины на основании выборки. Случайная величина X
- 6. Оценки параметров распределения Виды оценок: 1) Точечная оценка ã параметра a определяется одним числом, наиболее близким
- 7. Точечные оценки Точечная оценка ã параметра a представляет собой случайную величину на множестве выборок из одной
- 8. Точечная оценка математического ожидания Точечной оценкой математического ожидания M(X) случайной величины X является выборочное среднее: Выборочное
- 9. Точечная оценка дисперсии Точечной оценкой дисперсии D(X) случайной величины X является выборочная дисперсия: Выборочная дисперсия является
- 10. Точечная оценка дисперсии Точечной оценкой дисперсии D(X) случайной величины X является исправленная дисперсия: Исправленная дисперсия является
- 11. Точечная оценка среднего квадратического отклонения Точечной оценкой среднего квадратического отклонения σ(X) случайной величины X является исправленное
- 12. Точечная оценка среднего квадратического отклонения Несмещенной точечной оценкой среднего квадратического отклонения σ(X) случайной величины X является
- 13. Точечная оценка ско среднего арифметического Точечная оценка среднего квадратического отклонения среднего арифметического одинаково распределенных независимых случайных
- 14. Интервальные оценки Интервальная оценка параметра a задается в виде доверительного интервала [ã1; ã2] и доверительной вероятности
- 15. Интервал для значений случайной величины При нормальном распределении случайной величины X с математическим ожиданием M(X) и
- 16. Доверительный интервал для математического ожидания При нормальном распределении случайной величины X с математическим ожиданием M(X) и
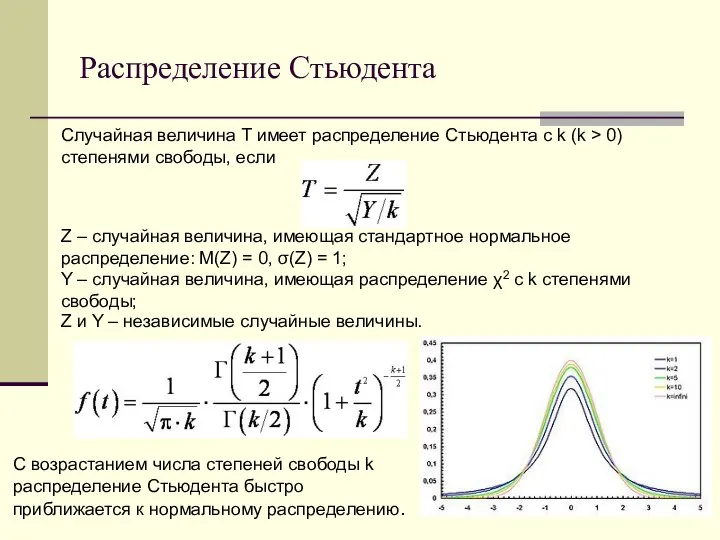
- 17. Распределение Стьюдента Случайная величина T имеет распределение Стьюдента с k (k > 0) степенями свободы, если
- 18. Доверительный интервал для среднего квадратического отклонения При нормальном распределении случайной величины X с ско σ(X) с
- 20. Скачать презентацию
















 Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? ttp_1
ttp_1 Блиц - турнир
Блиц - турнир Презентация на тему Диаграммы (6 класс)
Презентация на тему Диаграммы (6 класс)  Классификация измерений
Классификация измерений Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Начальные геометрические сведения (тест)
Начальные геометрические сведения (тест) Презентация на тему Делимое и делитель (2 класс)
Презентация на тему Делимое и делитель (2 класс) 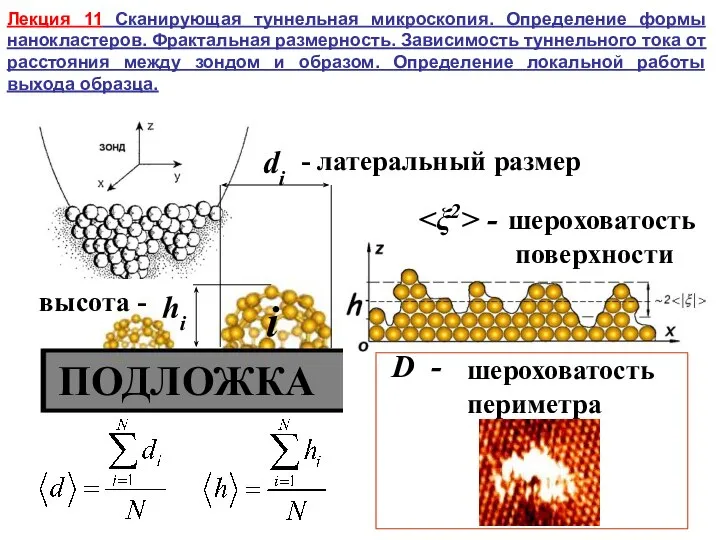 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Могла ли математика спасти Пахома, или Площадь
Могла ли математика спасти Пахома, или Площадь Квадратичная функция
Квадратичная функция Решение уравнений в целых числах
Решение уравнений в целых числах Приемы письменных вычислений
Приемы письменных вычислений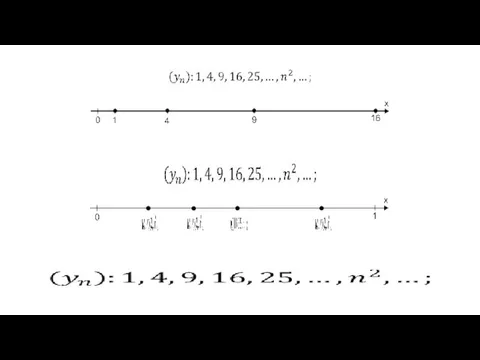 Пояснения к определению предела последовательности
Пояснения к определению предела последовательности Корни. Арифметический корень
Корни. Арифметический корень preobrazovanie
preobrazovanie Школьный портфель. Буква Ы. Счёт до 7
Школьный портфель. Буква Ы. Счёт до 7 Среднее арифметическое
Среднее арифметическое ЕГЭ 2020. Решение задания №9
ЕГЭ 2020. Решение задания №9 Степенные, показательные, логарифмические и тригонометрические функции
Степенные, показательные, логарифмические и тригонометрические функции Матричная алгебра. Лекция 2
Матричная алгебра. Лекция 2 Множества. 8 класс
Множества. 8 класс Геометрия прически
Геометрия прически Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Урок-экскурсия по государственному историко-культурному музею-заповеднику Московский Кремль
Урок-экскурсия по государственному историко-культурному музею-заповеднику Московский Кремль Решение уравнений «В мире звезд»
Решение уравнений «В мире звезд» Построение сечений многогранников. Задачи
Построение сечений многогранников. Задачи