Слайд 2СВОЙСТВА МЕДИАНЫ ТРЕУГОЛЬНИКА
Ключевые задачи
В треугольнике медианы пересекаются в одной точке и делятся

в отношении 2:1, считая от вершины.
Медиана делит треугольник на два равновеликих треугольника, а три медианы – на шесть равновеликих треугольников.
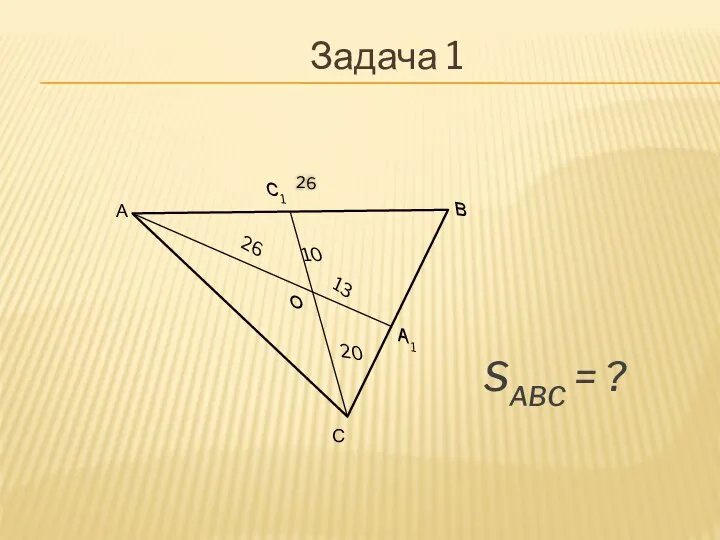
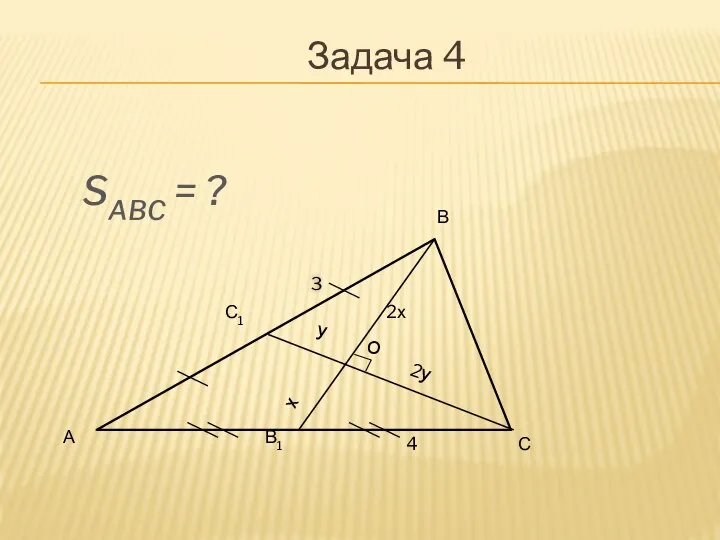
Если О – точка пересечения медиан треугольника АВС, то SАВС = 3SАОВ = 3SАОС = 3SВОС .
Слайд 7ДЛИНА МЕДИАНЫ ТРЕУГОЛЬНИКА
Ключевая задача
В треугольнике АВС со сторонами АВ=с, АС=b и ВС=а
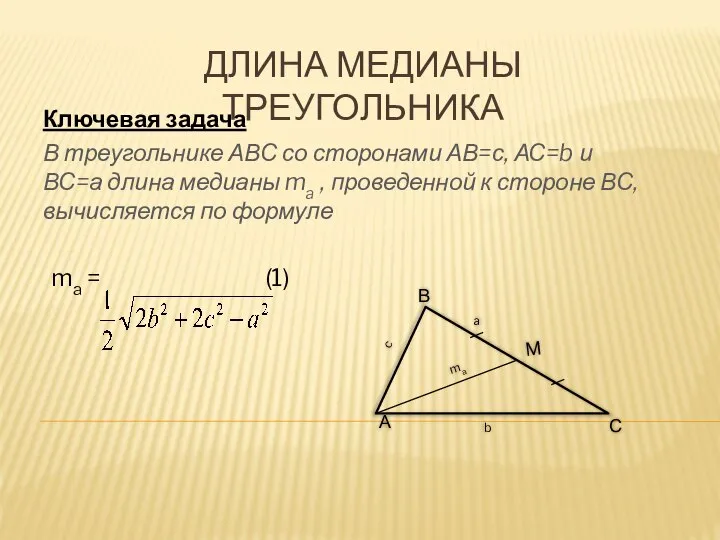
длина медианы ma , проведенной к стороне ВС, вычисляется по формуле
ma = (1)
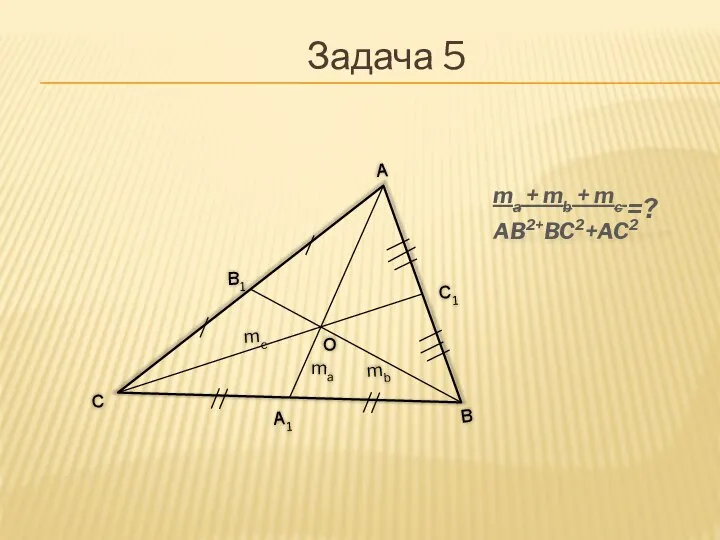
Слайд 8ma + mb + mc =?
AB2+BC2+AC2
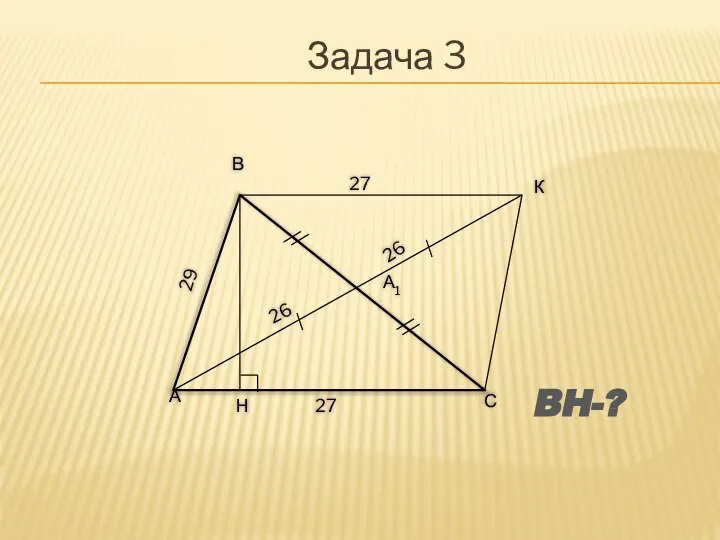
Задача 5



 Число 10
Число 10 Сумма углов в треугольнике
Сумма углов в треугольнике Перестановочные тесты и бутстреп анализ
Перестановочные тесты и бутстреп анализ Старинные меры длины на Руси
Старинные меры длины на Руси Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Устный счёт для дошкольников
Устный счёт для дошкольников Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности
Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности Графическое решение уравнений
Графическое решение уравнений Презентация на тему Типы параллелепипеда
Презентация на тему Типы параллелепипеда  Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Трапеция. Задачи по готовым чертежам
Трапеция. Задачи по готовым чертежам Морфизмы алгебр
Морфизмы алгебр Дополни до 10
Дополни до 10 Решение уравнений (2 класс)
Решение уравнений (2 класс) Задачи. вариант 3
Задачи. вариант 3 Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Стереометрические задачи повышенной сложности
Стереометрические задачи повышенной сложности Векторы
Векторы Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Взаимное пересечение двух поверхностей. Лекция 9
Взаимное пересечение двух поверхностей. Лекция 9 Начальные понятия геометрии
Начальные понятия геометрии Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни
Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни Преобразование обыкновенных дробей в десятичные
Преобразование обыкновенных дробей в десятичные Числа 1,2. Цифры 1,2
Числа 1,2. Цифры 1,2 Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Презентация на тему Арифметические действия с десятичными дробями
Презентация на тему Арифметические действия с десятичными дробями  Деление дробей
Деление дробей