Параллелепипед

Параллелепипед

Цели обучения:
10.1.2 знать определение и свойства прямоугольного параллелепипеда;
10.3.7 выводить свойства прямоугольного параллелепипеда и применять их при решении задач;

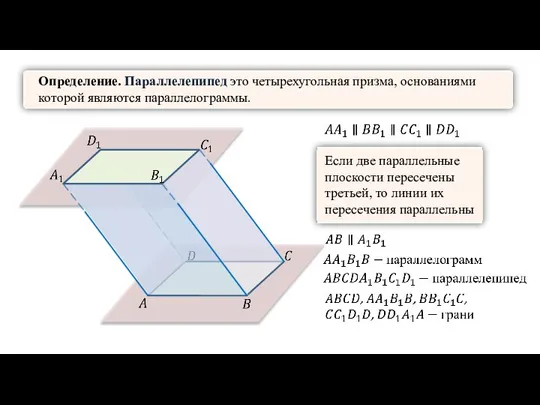
Определение. Параллелепипед это четырехугольная призма, основаниями которой являются параллелограммы.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

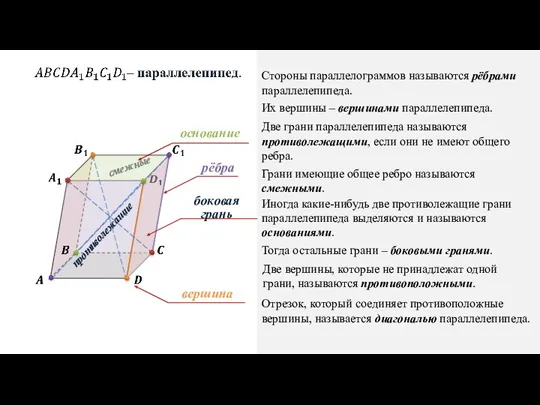
Стороны параллелограммов называются рёбрами параллелепипеда.
Их вершины – вершинами параллелепипеда.
Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра.
вершина
основание
рёбра
Грани имеющие общее ребро называются смежными.
противолежащие
смежные
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями.
Тогда остальные грани – боковыми гранями.
боковая
грань
Отрезок, который соединяет противоположные
вершины, называется диагональю параллелепипеда.
Две вершины, которые не принадлежат одной грани, называются противоположными.

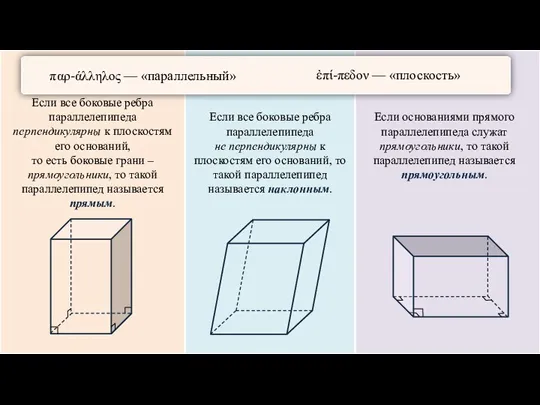
Если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований,
то есть боковые грани – прямоугольники, то такой параллелепипед называется прямым.
Если все боковые ребра параллелепипеда
не перпендикулярны к плоскостям его оснований, то такой параллелепипед называется наклонным.
Если основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
παρ-άλληλος — «параллельный»
ἐπί-πεδον — «плоскость»

1°. В прямоугольном параллелепипеде 6 граней и все они являются прямоугольниками.
2°. Противоположные грани попарно равны и параллельны.
3°. Все двугранные углы – прямые.
4°. Диагонали прямоугольного параллелепипеда равны.
5°. Прямоугольный параллелепипед имеет 4 диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6°. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7°. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8°. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Свойства прямоугольного параллелепипеда

Дано: АВСDА1В1С1D1 — параллелепипед
Доказать: теорема 1
Доказательство:
1) АВСD — параллелограмм ⇒ BC ∥ AD
2) АВВ1А1 — параллелограмм ⇒ ВВ1 ∥ AA1
4) ВС = АD, ВВ1 = АА1
5) ∠В1ВС = ∠А1АD
B
A
D
C
B1
C1
D1
A1
Ч.т.д
Теорема 1. Противоположные грани параллелепипеда параллельны и равны.

Дано: АВСDА1В1С1D1 — параллелепипед
Доказать: теорема 2
Доказательство:
1) ВB1 = AA1, ВB1 ∥ AA1
АА1 = DD1, АА1 ∥ DD1
4) BC1D1A — параллелограмм ⇒
2) ВВ1 = АА1, АА1 = DD1 ⇒ ВВ1 = DD1
Ч.т.д
A
D
C
B
A1
C1
B1
D1
В1D, BD1 — диагонали ВВ1D1D
ВВ1 ∥ АА1, АА1 ∥ DD1 ⇒ ВВ1 ∥ DD1 (если две прямые в пространстве параллельны третьей прямой, то они параллельны)
⇒ BB1D1D — параллелограмм ⇒
⇒ В1D ∩ BD1 = О,
В1О = ОD, BO = OD1 (диагонали параллелограмма пересекаются и точкой пересечения делятся пополам)
⇒ C1A ∩ BD1 = O,
C1O = OA, BO = OD1
O
Теорема 2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Задача 1
Дано: АВСDА1В1С1D1 — параллелепипед
Доказать: ALMDNB1C1P — параллелепипед
BL = CM = A1N = D1P
1) ВВ1А1А — параллелограмм ⇒ ВВ1 = АА1, ВВ1 ∥ АА1
4) MC1PD – параллелограмм (аналогично п. 3)
5) ∠LB1N = ∠MC1P
Доказательство:
A
B
C
D
D1
B1
C1
L
M
N
P
A1
⇒ LB1 = NA, LB1 ∥ NA
⇒ LB1NA — параллелограмм
8) A1N = D1P ⇒ NA1D1P — параллелограмм ⇒ A1D1 ∥ NP ∥ AD
9) (ABB1A1) ∥ (DCC1D1) ⇒ B1C1 = LM = AD = NP
10) ANPD, NB1C1P, LB1C1M, ALMD — параллелограммы
ALMDNB1C1P — параллелепипед
Что требовалось доказать

Доказательство.
Что и требовалось доказать.

Решение.

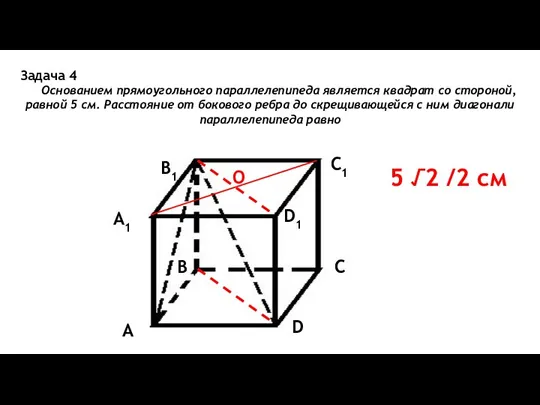
Задача 4
Основанием прямоугольного параллелепипеда является квадрат со стороной, равной 5 см. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно
A
B
C
D
A1
B1
C1
D1
5 √2 /2 см
О

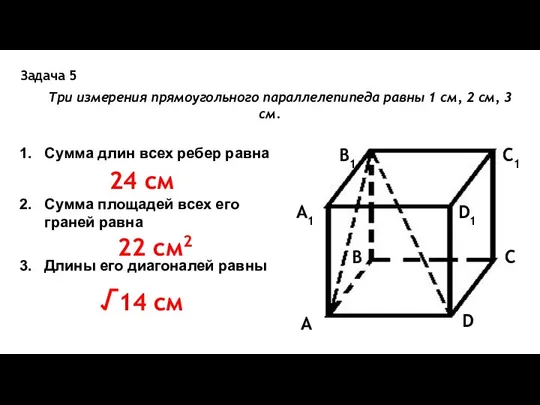
Задача 5
Три измерения прямоугольного параллелепипеда равны 1 см, 2 см, 3 см.
A
B
C
D
A1
B1
C1
D1
Сумма длин всех ребер равна
Сумма площадей всех его граней равна
Длины его диагоналей равны
24 см
22 см2
√14 см

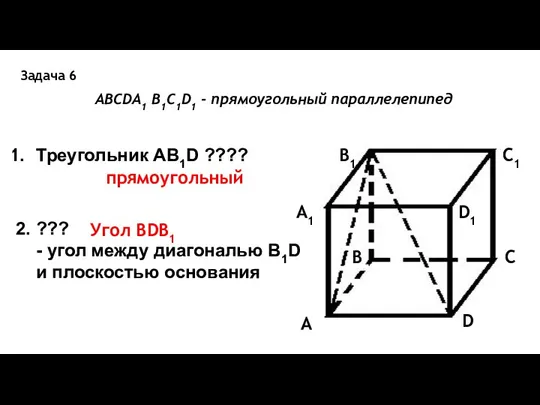
Задача 6
ABCDA1 B1C1D1 - прямоугольный параллелепипед
A
B
C
D
A1
B1
C1
D1
Треугольник AB1D ????
2. ???
- угол между диагональю B1D и плоскостью основания
прямоугольный
Угол BDB1