Слайд 2Цели урока
обучающая: сформулировать понятие параллельного проектирования; формировать у учащихся умение применять понятия

и свойства параллельного проектирования к решению задач;
развивающая: развивать абстрактное мышление, пространственное воображение и интуицию;
воспитательная: содействовать формированию и развитию ответственности, познавательного интереса к изучаемой дисциплине.
Слайд 3Параллельное проектирование
Пусть π - некоторая плоскость, l - пересекающая ее прямая.
a//l
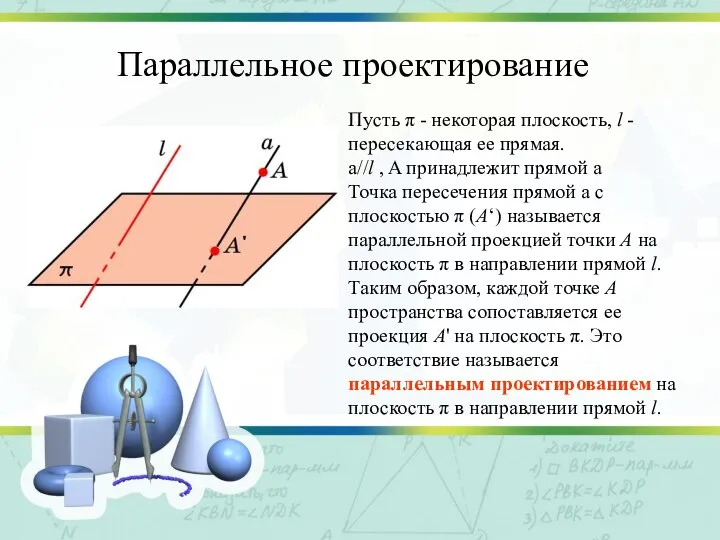
, A принадлежит прямой a
Точка пересечения прямой a с плоскостью π (A‘) называется параллельной проекцией точки A на плоскость π в направлении прямой l.
Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость π. Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l.
Слайд 4Свойство №1
Если прямая параллельна или совпадает с прямой l, то ее проекцией
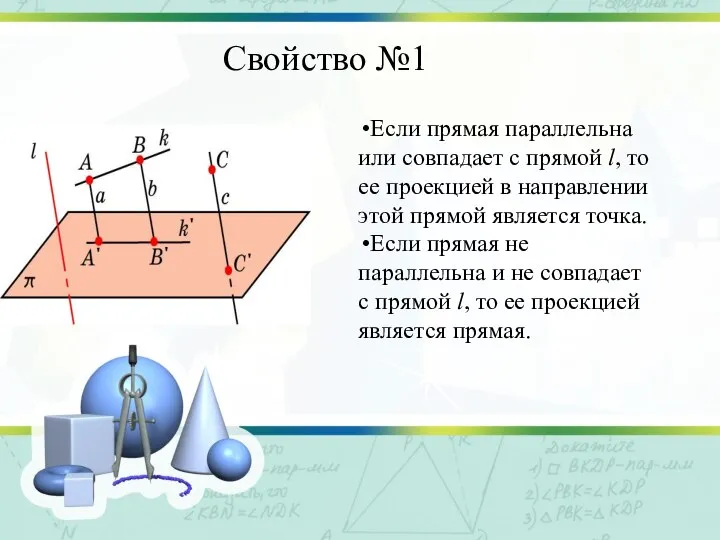
в направлении этой прямой является точка.
Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Слайд 5Свойство №2
Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой.
В
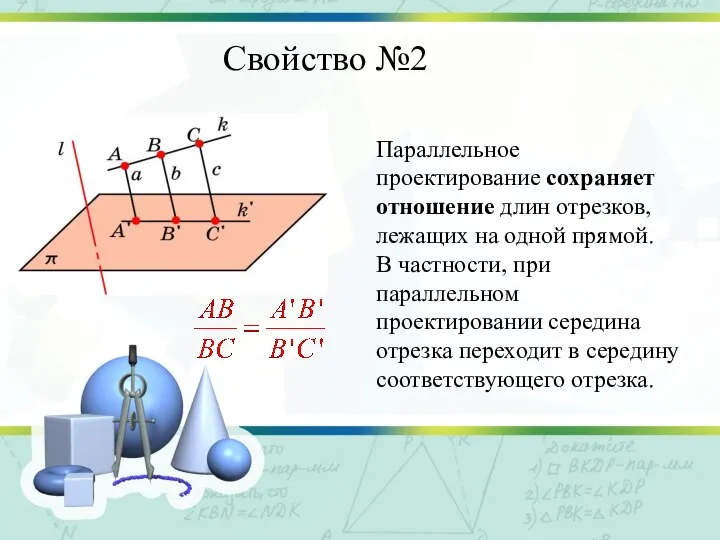
частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
Слайд 6Свойство №3
Если две параллельные прямые не параллельны прямой l, то их проекциями
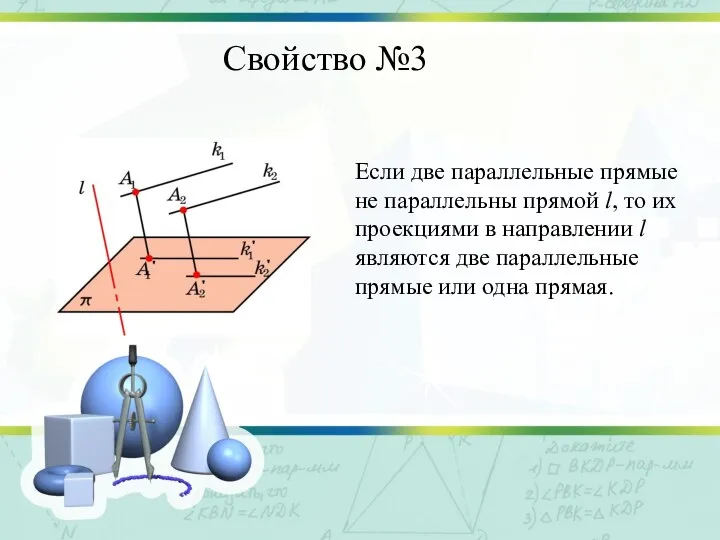
в направлении l являются две параллельные прямые или одна прямая.
Слайд 7Ортогональная проекция точки
Ортогональной проекцией точки А на данную плоскость называется проекция точки
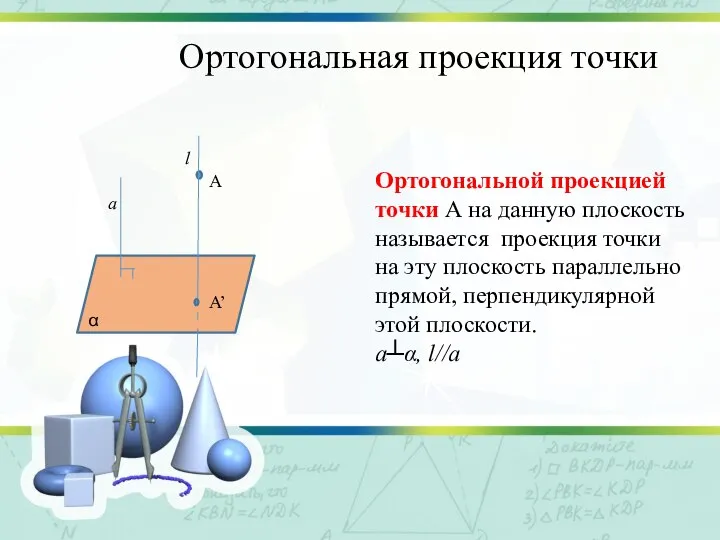
на эту плоскость параллельно прямой, перпендикулярной этой плоскости.
a┴α, l//a
Слайд 8Ортогональная проекция фигуры
Ортогональной проекцией фигуры на данную плоскость состоит из ортогональных проекций
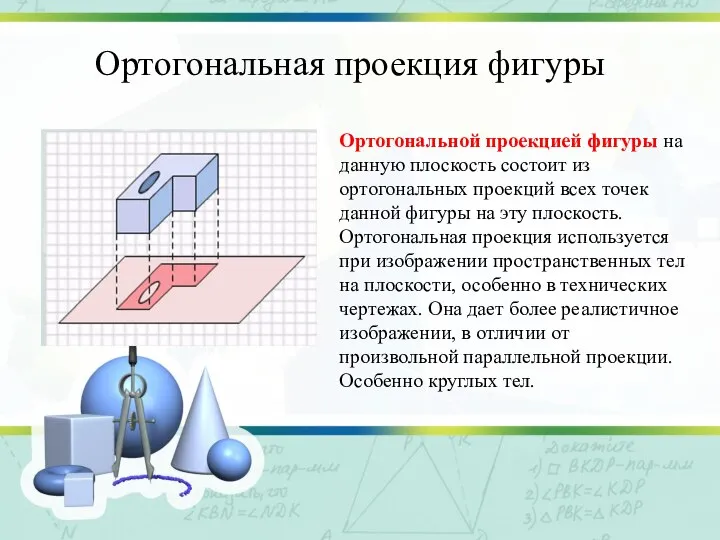
всех точек данной фигуры на эту плоскость. Ортогональная проекция используется при изображении пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистичное изображении, в отличии от произвольной параллельной проекции. Особенно круглых тел.
Слайд 9Соотношения пространственных фигур
их изображениям на плоскости
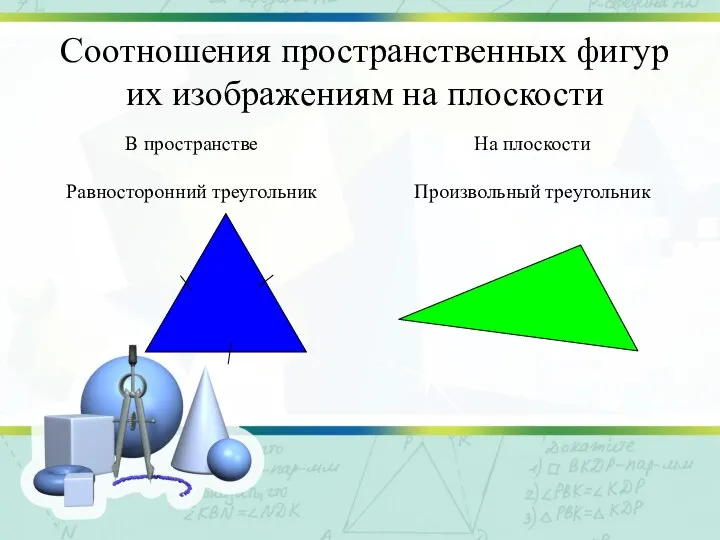
Слайд 10Соотношения пространственных фигур
их изображениям на плоскости
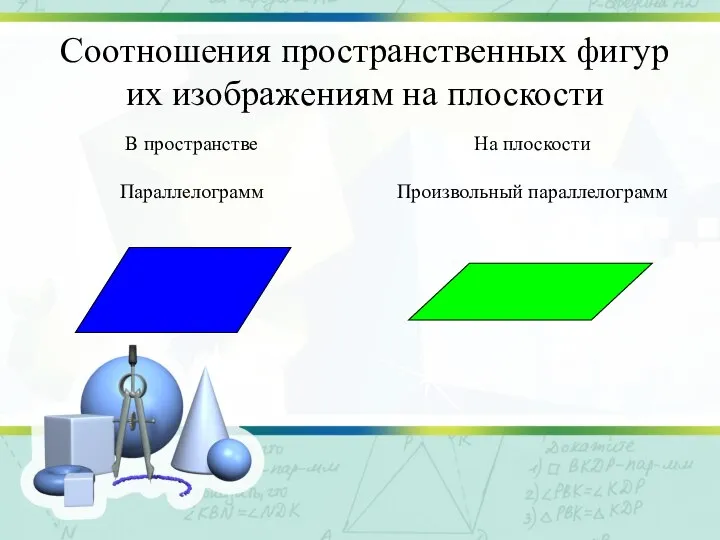
Слайд 11Соотношения пространственных фигур
их изображениям на плоскости
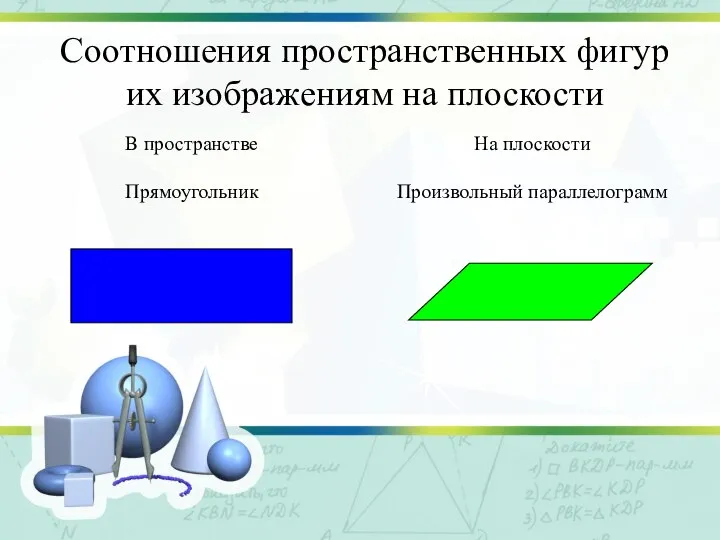
Слайд 12Соотношения пространственных фигур
их изображениям на плоскости
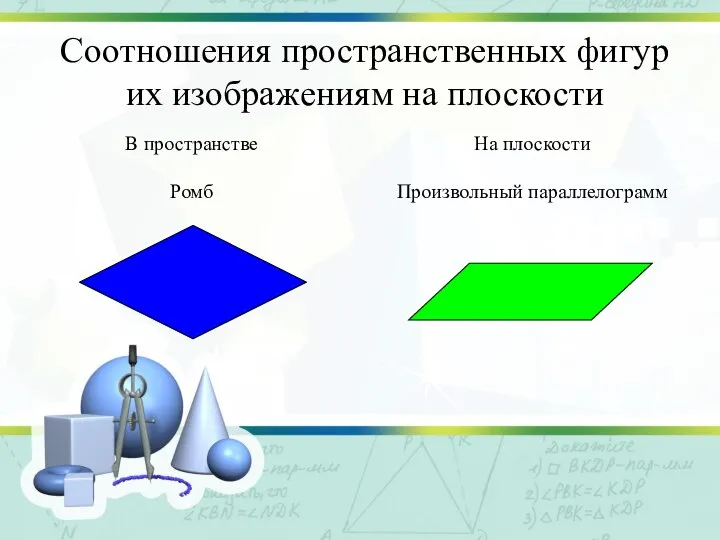
Слайд 13Соотношения пространственных фигур
их изображениям на плоскости
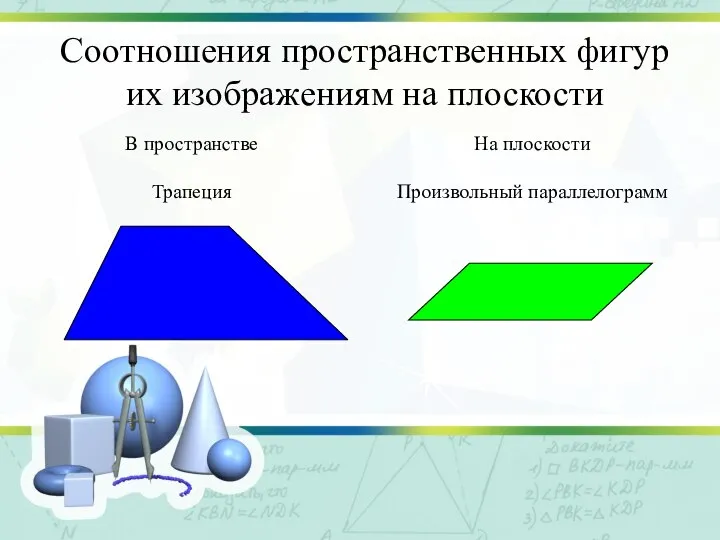
Слайд 14Соотношения пространственных фигур
их изображениям на плоскости
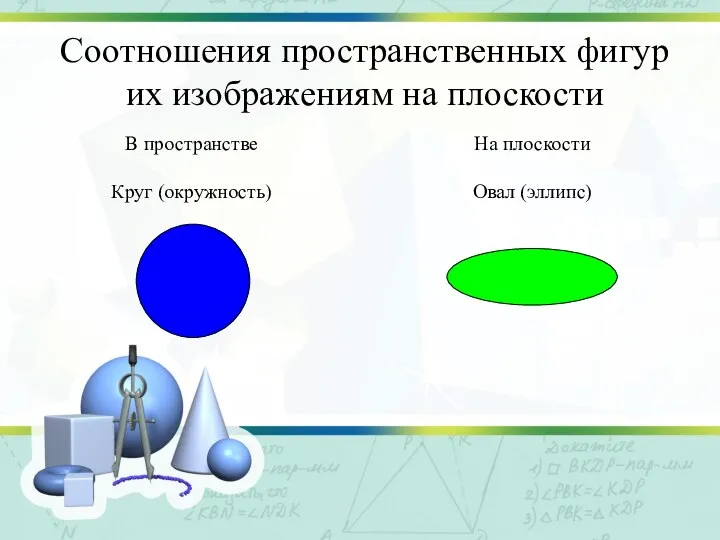
Слайд 15Алгоритм построения изображения пирамиды
Изображение пирамиды всегда начинают с изображения ее основания. Вершины
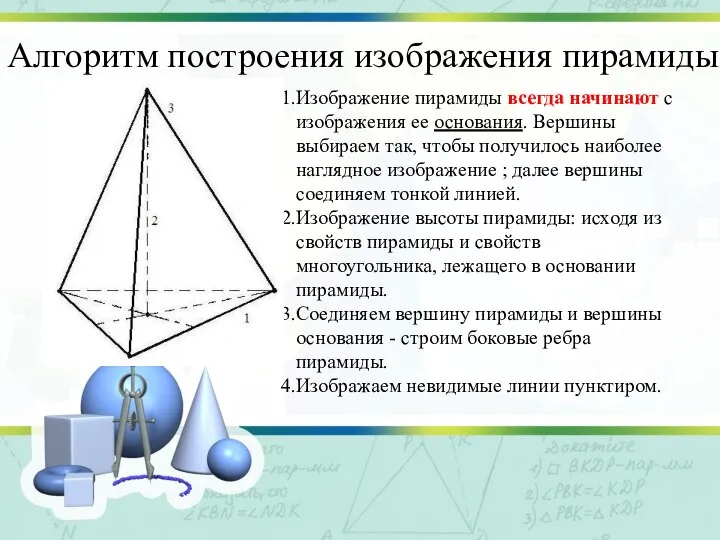
выбираем так, чтобы получилось наиболее наглядное изображение ; далее вершины соединяем тонкой линией.
Изображение высоты пирамиды: исходя из свойств пирамиды и свойств многоугольника, лежащего в основании пирамиды.
Соединяем вершину пирамиды и вершины основания - строим боковые ребра пирамиды.
Изображаем невидимые линии пунктиром.
Слайд 16Алгоритм изображения призмы
Изображение призмы всегда начинают с изображения ее основания. Вершины выбираем
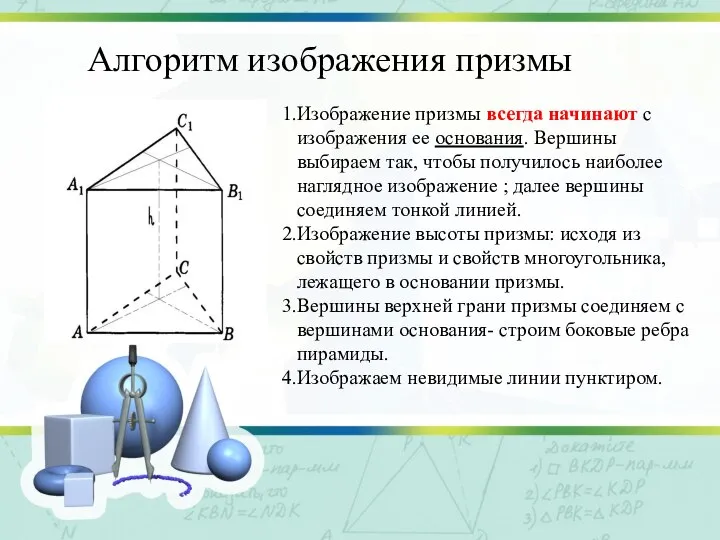
так, чтобы получилось наиболее наглядное изображение ; далее вершины соединяем тонкой линией.
Изображение высоты призмы: исходя из свойств призмы и свойств многоугольника, лежащего в основании призмы.
Вершины верхней грани призмы соединяем с вершинами основания- строим боковые ребра пирамиды.
Изображаем невидимые линии пунктиром.















 Задачи и примеры
Задачи и примеры Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Формулы приведения
Формулы приведения Решение задач. Линейные динамические системы
Решение задач. Линейные динамические системы Марионетки на нашем уроке математики
Марионетки на нашем уроке математики Объемы. Объем параллелепипеда
Объемы. Объем параллелепипеда Тренажёр. Табличное умножение. В сказочном лесу
Тренажёр. Табличное умножение. В сказочном лесу Вертикальные углы равны
Вертикальные углы равны Многозначные числа. Тест
Многозначные числа. Тест Презентация на тему Квадратные корни. Арифметический квадратный корень
Презентация на тему Квадратные корни. Арифметический квадратный корень  Презентация на тему Сложение чисел с разными знаками
Презентация на тему Сложение чисел с разными знаками  Распознавание и называние геометрических фигур
Распознавание и называние геометрических фигур Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.)
Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.) Дополнительные свойства вычисления пределов для дробно - рациональных функций
Дополнительные свойства вычисления пределов для дробно - рациональных функций Конус. Основные элементы конуса
Конус. Основные элементы конуса 1 замечательный предел
1 замечательный предел Презентация на тему Старинные меры длины
Презентация на тему Старинные меры длины  Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств АЛГОРИТМ ЕВКЛИДА
АЛГОРИТМ ЕВКЛИДА Цифры (дойти до апельсина)
Цифры (дойти до апельсина) Презентация на тему Подготовка к ГИА 2013
Презентация на тему Подготовка к ГИА 2013  Симметрия в окружающем мире
Симметрия в окружающем мире Таблица умножения с числом 3
Таблица умножения с числом 3 Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 О треугольниках
О треугольниках Додавання, редагування та формування таблиць
Додавання, редагування та формування таблиць Рациональные и иррациональные числа
Рациональные и иррациональные числа Решение систем неравенств (9 класс)
Решение систем неравенств (9 класс)