Содержание
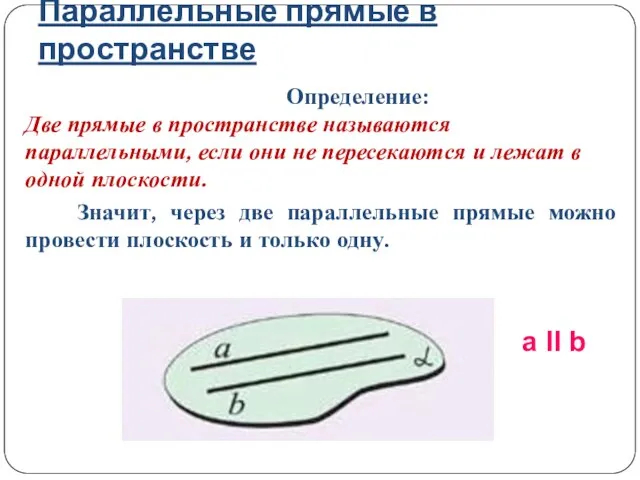
- 2. Параллельные прямые в пространстве Определение: Две прямые в пространстве называются параллельными, если они не пересекаются и
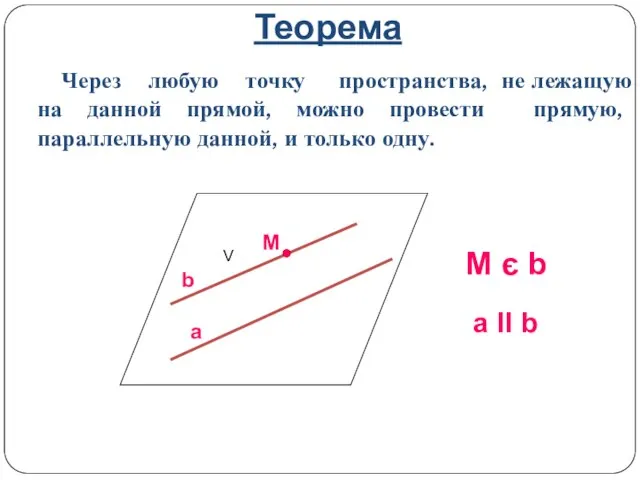
- 3. Теорема Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и
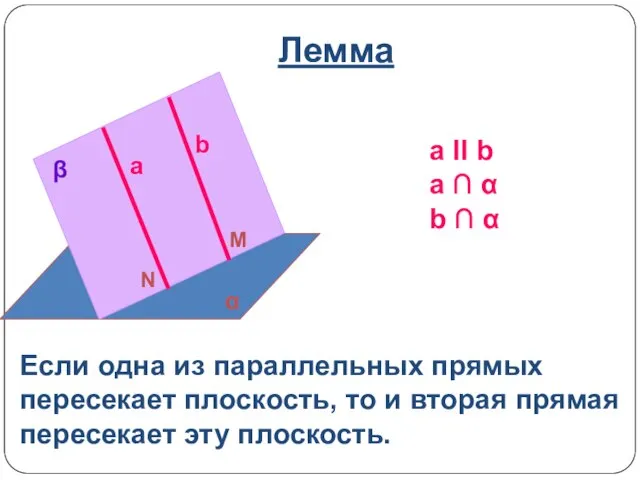
- 4. Лемма a ΙΙ b a ∩ α b ∩ α Если одна из параллельных прямых пересекает
- 5. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Если две прямые параллельны третьей прямой, то они параллельны между собой. a ΙΙ
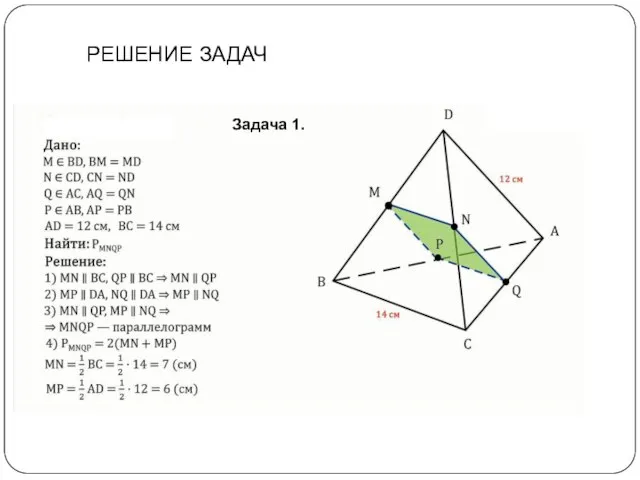
- 6. Задача 1. РЕШЕНИЕ ЗАДАЧ
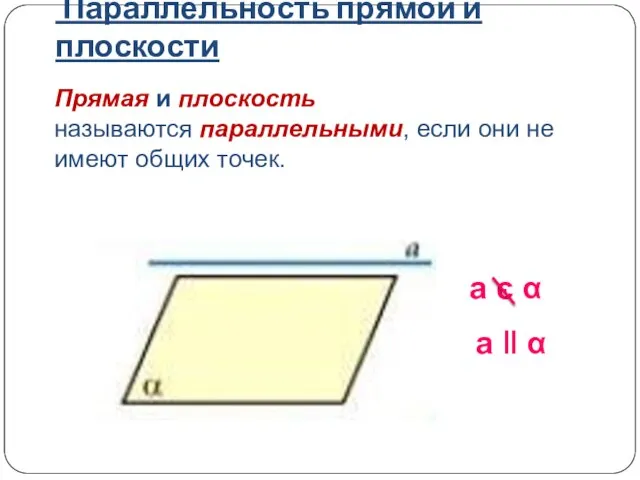
- 7. Прямая и плоскость называются параллельными, если они не имеют общих точек. a є α a ǁ
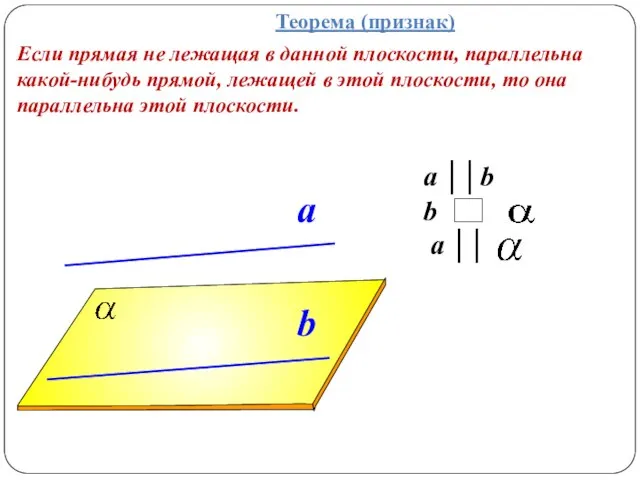
- 8. a ││b b a ││ a b Теорема (признак) Если прямая не лежащая в данной плоскости,
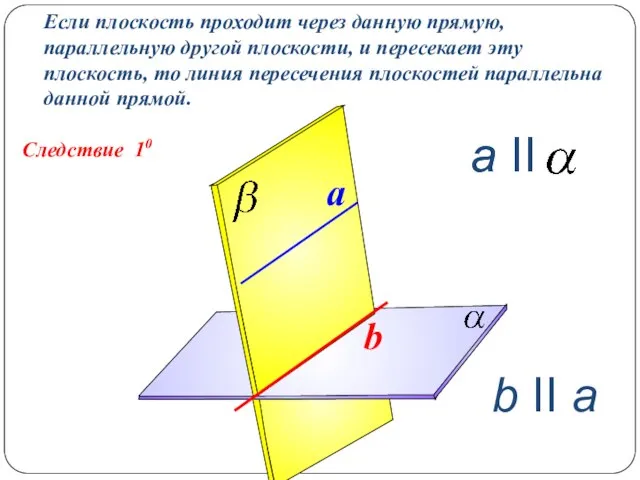
- 9. Следствие 10 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то
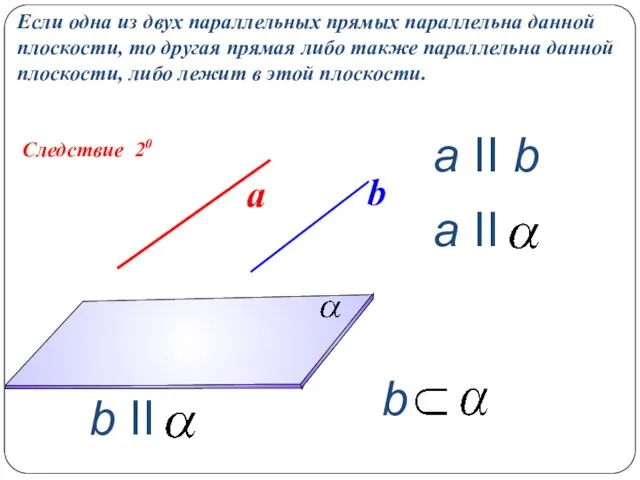
- 10. Следствие 20 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также
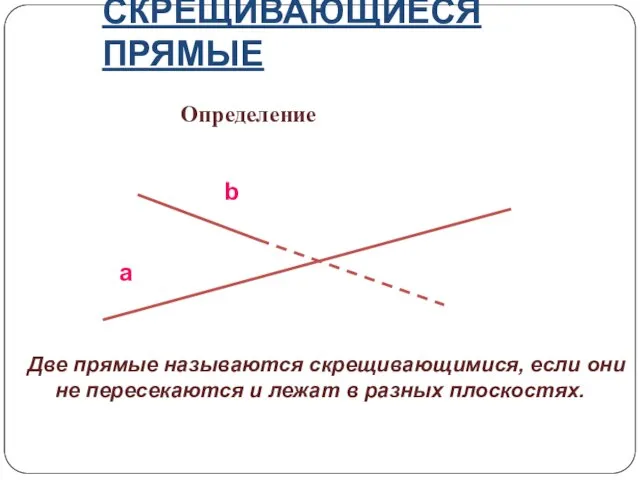
- 11. СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Определение a b Две прямые называются скрещивающимися, если они не пересекаются и лежат в
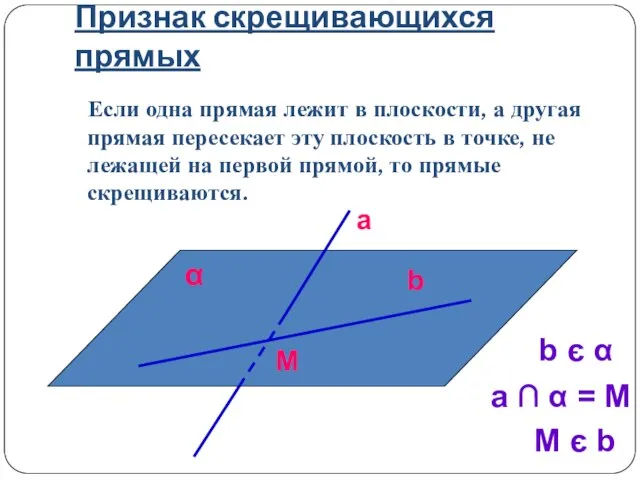
- 12. Признак скрещивающихся прямых Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в
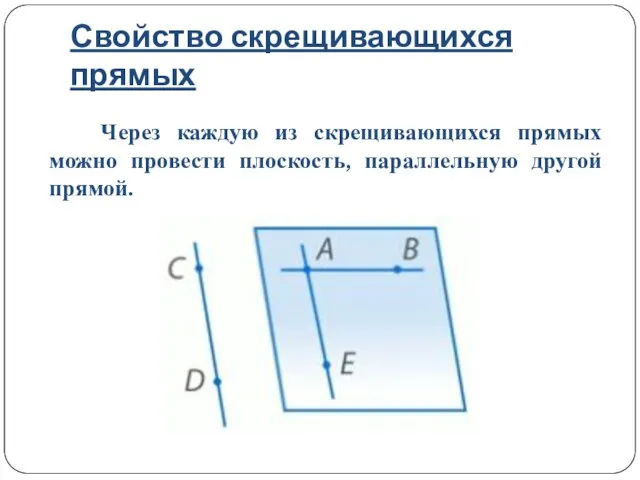
- 13. Свойство скрещивающихся прямых Через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
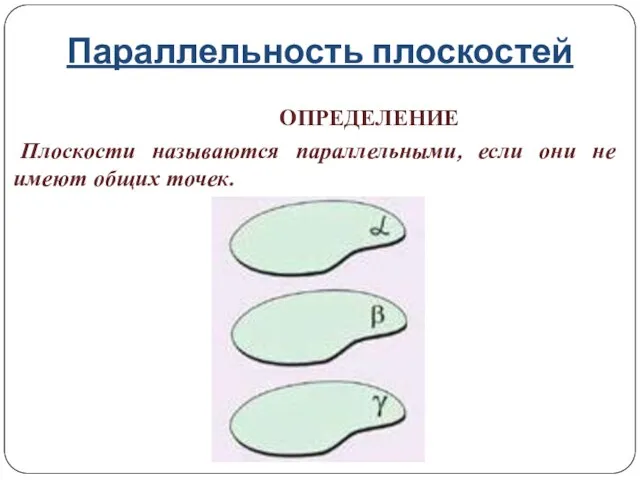
- 14. Параллельность плоскостей ОПРЕДЕЛЕНИЕ Плоскости называются параллельными, если они не имеют общих точек.
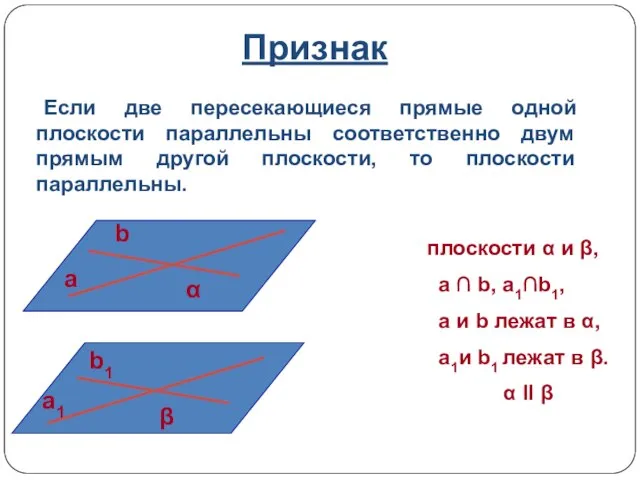
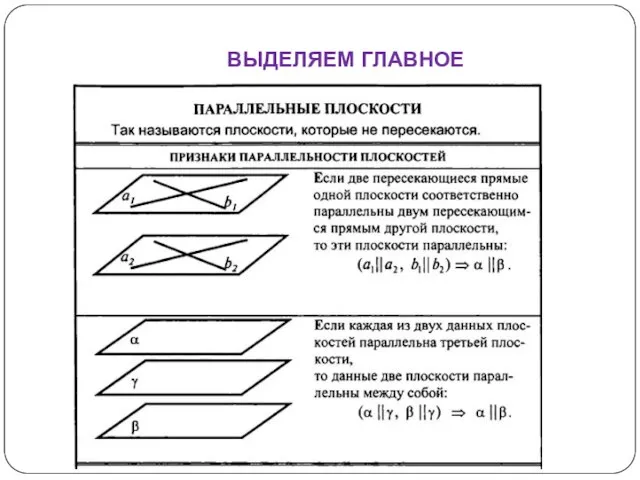
- 15. Признак плоскости α и β, a ∩ b, a1∩b1, a и b лежат в α, a1и
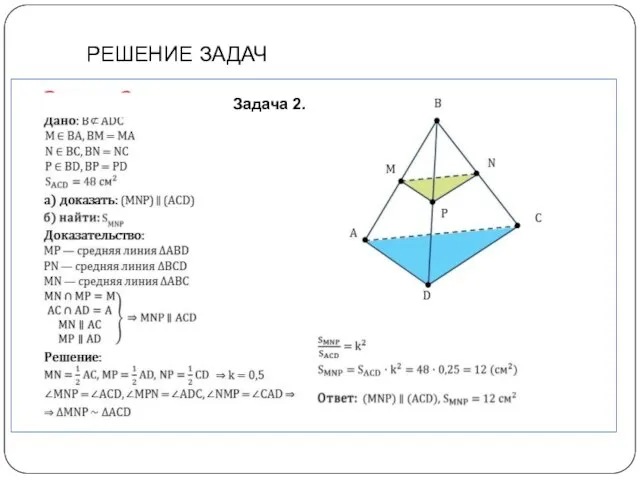
- 16. РЕШЕНИЕ ЗАДАЧ Задача 2.
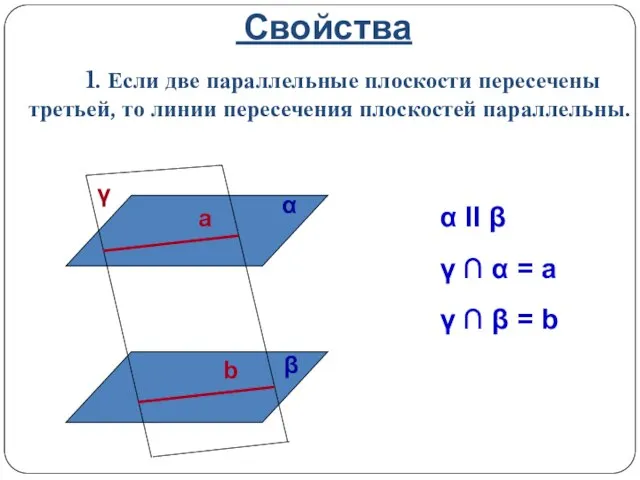
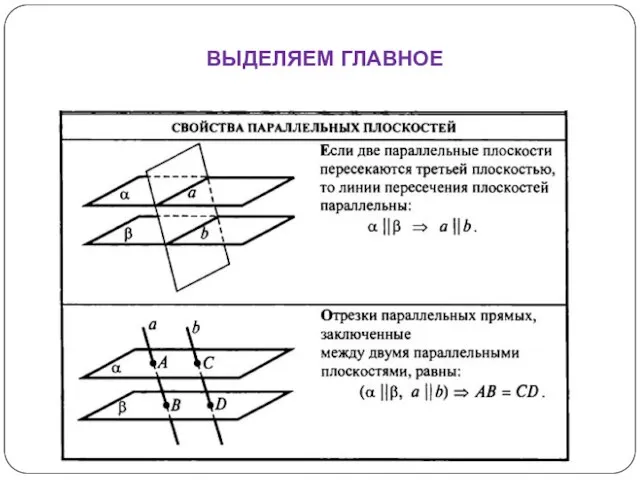
- 17. Свойства 1. Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны. α II β
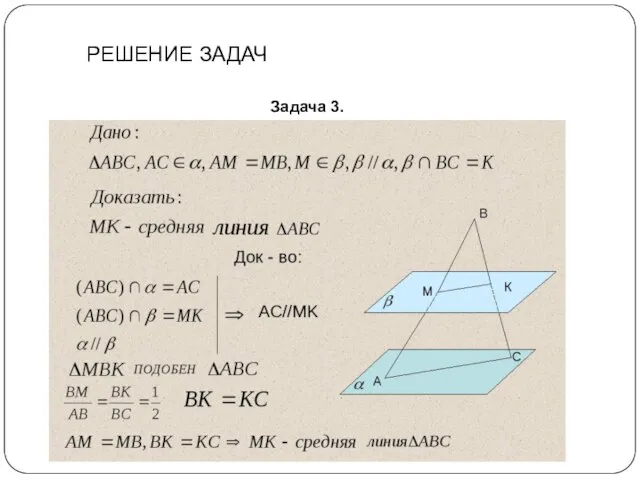
- 18. Задача 3. РЕШЕНИЕ ЗАДАЧ
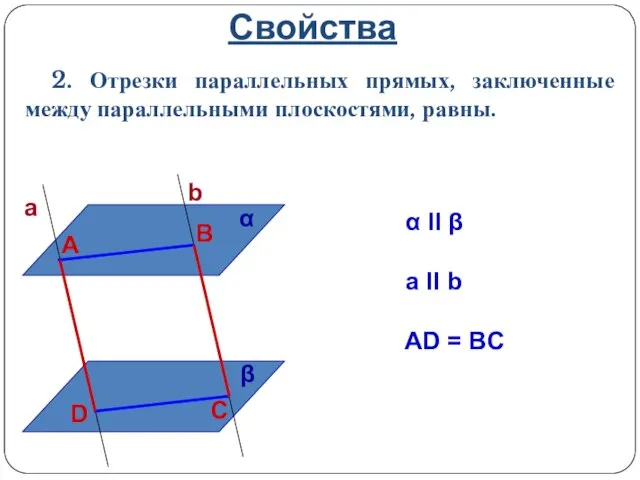
- 19. Свойства 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. α II β a II b
- 20. ВЫДЕЛЯЕМ ГЛАВНОЕ
- 21. ВЫДЕЛЯЕМ ГЛАВНОЕ
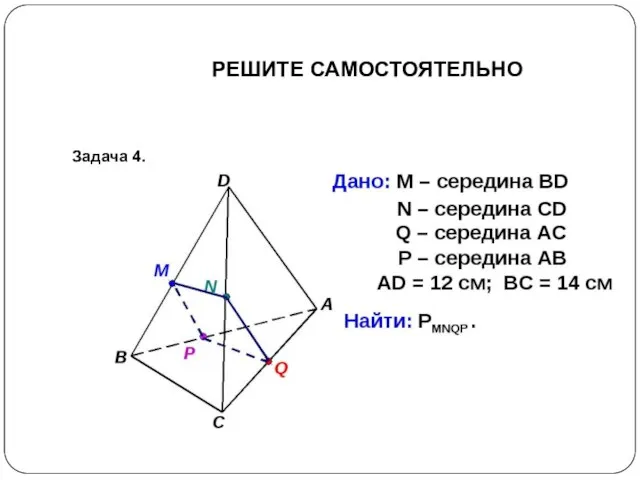
- 22. РЕШИТЕ САМОСТОЯТЕЛЬНО Задача 4.
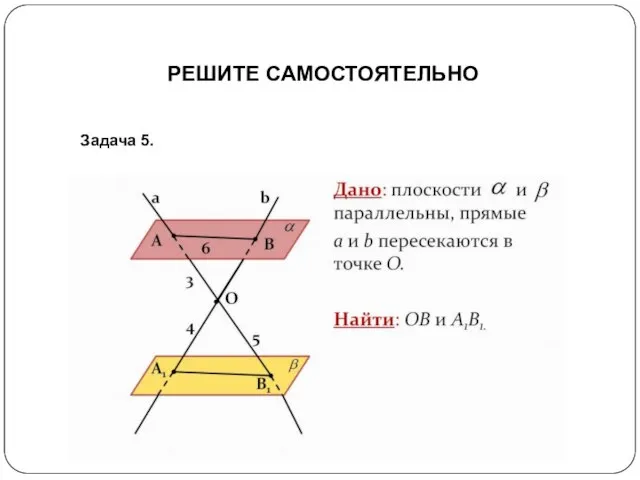
- 23. РЕШИТЕ САМОСТОЯТЕЛЬНО Задача 5.
- 25. Скачать презентацию

 Окружность. Теоремы
Окружность. Теоремы Понятие предиката и кванторы. Логические операции над предикатами
Понятие предиката и кванторы. Логические операции над предикатами Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА
Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА  Формула суммы п первых членов геометрической прогрессии
Формула суммы п первых членов геометрической прогрессии Решаем примеры
Решаем примеры Точки экстремума функции
Точки экстремума функции Сечения пространственных фигур
Сечения пространственных фигур Логарифмы. Свойства логарифмов
Логарифмы. Свойства логарифмов д.з
д.з Как можно сравнивать размеры больших и малых тел
Как можно сравнивать размеры больших и малых тел Вписанная и описанная окружности
Вписанная и описанная окружности Галерея великих имён
Галерея великих имён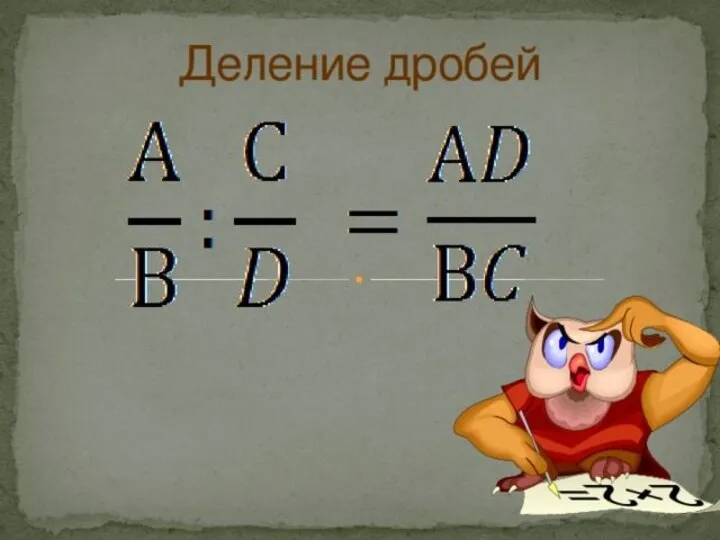 Деление дробей
Деление дробей Реляционная алгебра
Реляционная алгебра Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Конические сечения и их применения в технике
Конические сечения и их применения в технике Сокращение дробей. Тождество
Сокращение дробей. Тождество Презентация на тему Геометрия и лист бумаги 7 класс
Презентация на тему Геометрия и лист бумаги 7 класс  Обеспечение условий для максимально возможного раскрытия потенциала учащихся средствами математики
Обеспечение условий для максимально возможного раскрытия потенциала учащихся средствами математики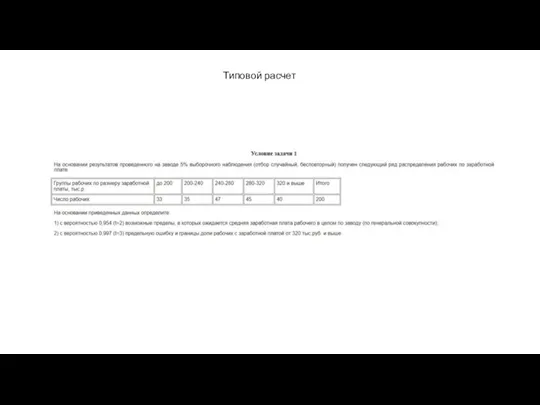 Типовой расчет. Часть 1
Типовой расчет. Часть 1 Дециметр
Дециметр Знакопостоянные числовые ряды. Лекция 1
Знакопостоянные числовые ряды. Лекция 1 Построение треугольника
Построение треугольника Автоматизация ректификационной колонны К-2 установки сернокислотного алкилирования Л-25/7
Автоматизация ректификационной колонны К-2 установки сернокислотного алкилирования Л-25/7 Взаимно-обратные задачи. 2 класс
Взаимно-обратные задачи. 2 класс Вычисления с многозначными числами
Вычисления с многозначными числами Прямоугольный параллелепипед
Прямоугольный параллелепипед Число 10. Запись числа 10
Число 10. Запись числа 10