Содержание
- 2. теоремы Пифагора По следам
- 3. Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни. О ней писали
- 4. Теорема Пифагора - одна из главных теорем геометрии. Если дан нам треугольник И при том с
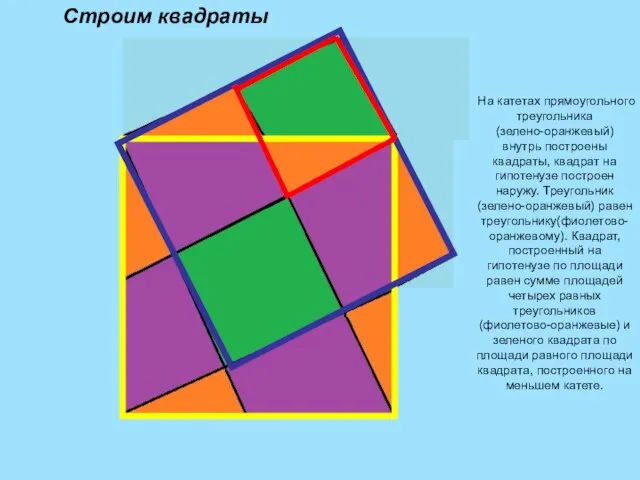
- 5. Строим квадраты На катетах прямоугольного треугольника (зелено-оранжевый) внутрь построены квадраты, квадрат на гипотенузе построен наружу. Треугольник
- 6. Строим квадраты D Из рисунка видно, что два квадрата, построенных на двух катетах и квадрат, построенный
- 7. Доказательство теоремы Пифагора в картинках. Красной краски, затраченной на то, чтобы покрасить квадрат, построенный на гипотенузе
- 8. Итак, в прямоугольном треугольнике a² + b² = c² Если есть фигуры А,В и С, площади
- 9. c a b c b c a b c a b c b b b b
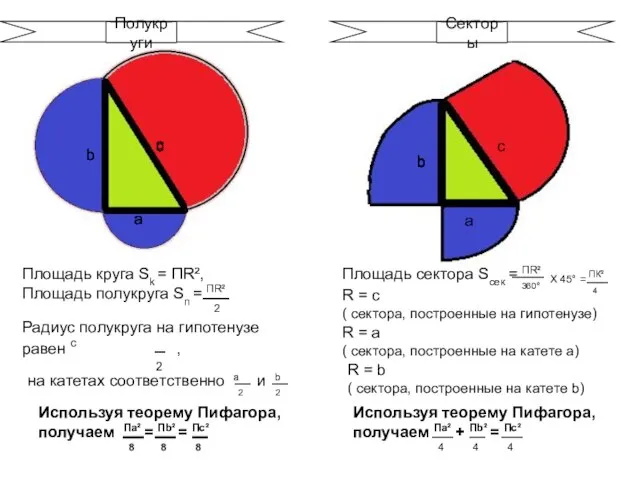
- 10. На рис. 10, 11, 12 изображены по три равновеликие фигуры.
- 11. Мобильная связь Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в
- 13. Скачать презентацию








 Свойства логарифмов
Свойства логарифмов Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Координатная плоскость
Координатная плоскость Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Справочник по геометрии
Справочник по геометрии Презентация на тему Высказывания со словами: есть, существует, некоторые
Презентация на тему Высказывания со словами: есть, существует, некоторые  Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши)
Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши) Решение задач по теме: Объем цилиндра 11 класс
Решение задач по теме: Объем цилиндра 11 класс Распределительное свойства умножения
Распределительное свойства умножения Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Задания по геометрии
Задания по геометрии Составление алгоритма
Составление алгоритма Конус
Конус Логарифмические уравнения
Логарифмические уравнения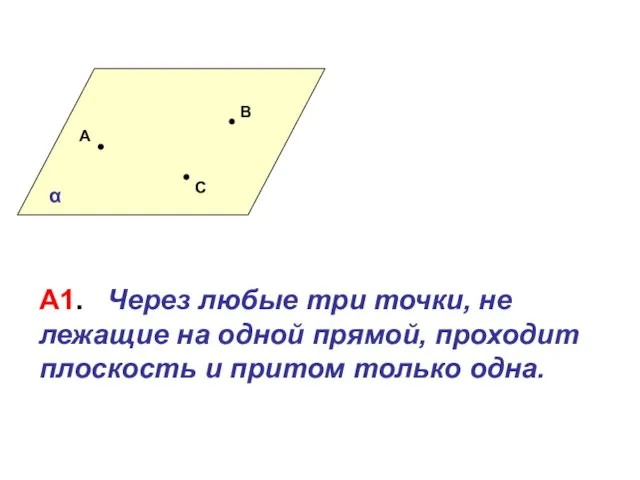 Плоскости
Плоскости Комплексные числа и действия над ними
Комплексные числа и действия над ними Найди значение выражений
Найди значение выражений Размерность. Единицы измерения
Размерность. Единицы измерения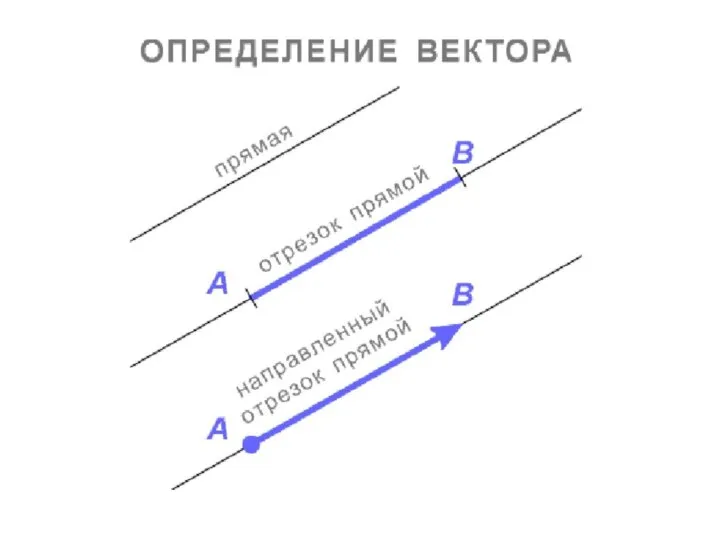 Определение вектора
Определение вектора Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Понятие цилиндра
Понятие цилиндра Коэффициент корреляции
Коэффициент корреляции Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Системы степенных неравенств
Системы степенных неравенств