Теория вероятностей. Поток событий

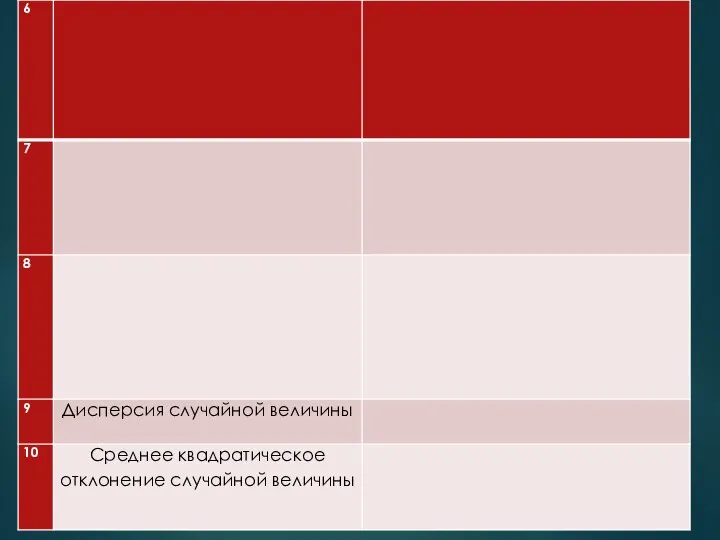
Характеристики случайной величины Χ(t0, τ)

С какой вероятностью:
1. За ноябрь месяц поступит в компанию 6 требований?
2. За декабрь месяц поступит в компанию 6 требований?
3. За январь месяц поступит не менее пяти требований?
4. За первые две недели ноября не поступит ни одного требования?
5. За вторую и третью недели декабря поступит хотя бы одно требование?
6. Интервал времени между двумя соседними поступлениями требований будет не менее трёх дней, если первое из них поступило в первый день второй недели января?
7. Интервал времени между двумя соседними поступлениями требований будет меньше двух дней, если первое из них поступило в начале третьей недели декабря?

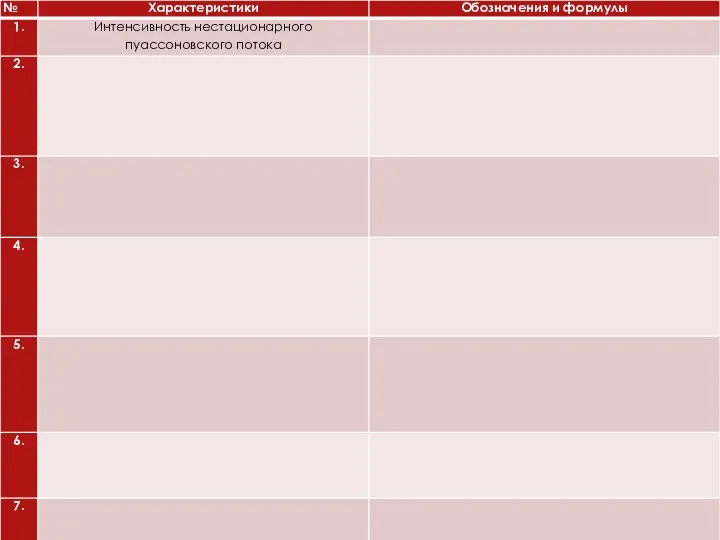
Пусть П - поток требований по выплатам, поступающих в страховую компанию. Поток П без последствий и ординарен, т.е является пуассоновским . Но в отличие от потока в предыдущей задаче данный поток уже не будет стационарным и, следовательно, не будет простейшим.

Решение
Месяцы, разбитые на недели, в которые анализируется поток поступлений в страховую компанию требований по выплатам.