Содержание
- 2. Содержание Первообразная Интеграл а) неопределённый б) определённый
- 3. Первообразная
- 4. Определение Функция F(х) называется первообразной функции f(х) на промежутке Х, если На практике промежуток Х обычно
- 5. Теорема 1 Если функция f(х) непрерывна при , то для f(х) существует первообразная F(х) на Х.
- 6. Теорема 2 Если F(x) одна из первообразных функции f(x), на промежутке Х, то у функции у
- 7. Таблица первообразных Зная формулы для нахождения производных, можно составить таблицу для нахождения первообразных
- 8. Правила нахождения первообразных Первообразная суммы равна сумме первообразных Если F(x) – первообразная для f(x), то к·F(x)
- 9. Найдём одну из первообразных Если f(x) равно: 1) f(x)=2х+х³ 2) f(x)=4х-2 3) f(x)=х³-3х²+х-1 4) f(x)=4х⁵+2х+е 5)
- 10. Ответить на вопрос: какая функция является перообразной для функции f(x)= 2sinx – cosx? А) cosx -
- 11. Выберите ответ, при котором предложение будет верно. Функция F(x) является первообразной для функции f(x), если: А)
- 12. Ответить на вопрос: для какой функции первообразной является функция F(x)=2x³+6x²+x-9? А) f(x) = 1/4·x⁴+2x³+x²-9x Б) f(x)
- 13. Ответить на вопрос: производная какой из функций равна у = 4х - 3х²? А) F(x) =
- 14. Задание №1. Найдите первообразную функции f(x), график которой проходит через точку А. а) f(x)=5х+х², А(0;3) б)
- 15. б) f(x)=3х - 5, А(4;10) Решение. F(x)= 3х²⁄2-5х+С, где С – произв. число. F(4)= 3·4²⁄2-5·4+С=24-20+С=4+С и
- 16. Самостоятельно Найдите первообразную функции f(x), график которой проходит через точку А, если: 1) f(x)=х²-5, А(3;4) 2)
- 17. Проверим ответы 1) F(x)= х³⁄3 - 5х + 10 2) F(x)= 2х³⁄3 + 3х + 6(1/3)
- 18. Задание №2. Найдите первообразную функции f(x), значение которой при х = х₀ равно у₀. а) f(x)=10х⁴+х;
- 19. б) f(x)=2sin3x+4cos(x/2); х₀=π⁄3; у₀=0 Решение. F(x)=-2·1/3·cos3x+4·2 sin(x/2)+С= =-2/3·cos3x+8· sin(x/2)+С, где С- пр. ч. Найдём С. Т.к.
- 20. в) f(x)=4+6х²; х₀=2; у₀ Решение. F(x)= 4х+6х³⁄3+С, где С-п.ч. Найдём С: т.к. F(х₀)= у₀ , то
- 21. г) f(x)=2х³+х²+3; х₀=1; у₀>0 Решение. F(x)= 2х⁴⁄4+х³⁄3+3х+С, где С- пр.ч. Найдём С. F(1)= 2·1⁴⁄4+1³⁄3+3·1+С = 3(5/6)+С,
- 22. Задание №3. Найдите множество первообразных функции f(x). а) f(x) =sin²x б) f(x) = sin5x·cos6x Решение. а)
- 23. б) f(x) = sin5x·cos6x Решение. т.к. f(x) = sin5x·cos6x = =1/2·(sin11x-sinx), то множество всех первообразных данной
- 24. ИНТЕГРАЛЫ
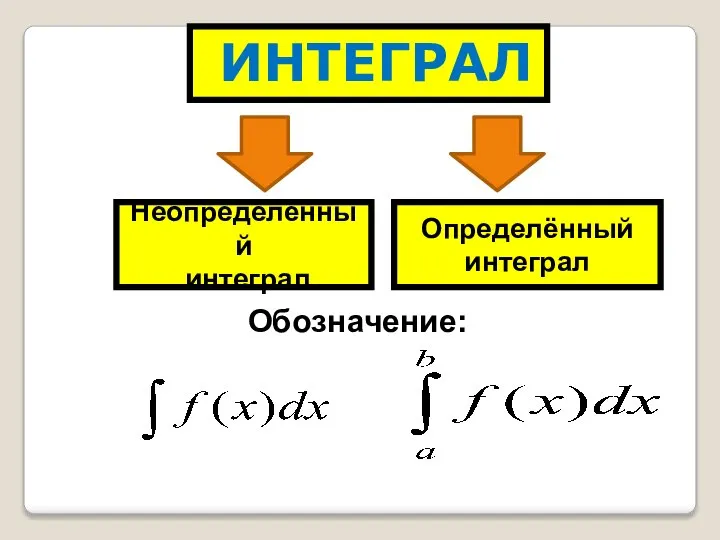
- 25. ИНТЕГРАЛ Неопределённый интеграл Определённый интеграл Обозначение:
- 26. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- 27. Определение: Множество всех первообразных функции f(x) на некотором промежутке называется неопределенным интегралом от функции f(x) на
- 28. Основные свойства неопределенного интеграла. т.е. постоянный множитель можно выносить за знак интеграла
- 29. Основные свойства неопределенного интеграла.
- 30. Таблица основных неопределённых интегралов
- 32. Таблица интегралов
- 33. Определение Процесс нахождения интеграла называется интегрированием Интегрирование является операцией, обратной дифференцированию
- 34. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- 35. Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и пусть F(x) – некоторая ее
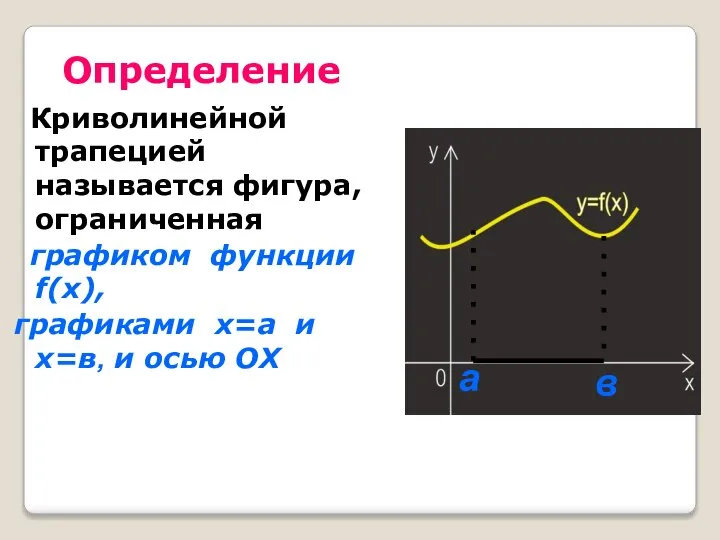
- 36. Определение Криволинейной трапецией называется фигура, ограниченная графиком функции f(x), графиками х=а и х=в, и осью ОХ
- 37. Формула Ньютона-Лейбница Теорема: если функция у = f(x) непрерывна на отрезке [а;в], то справедлива формула Опираясь
- 38. Свойства определенного интеграла
- 39. Свойства определенного интеграла
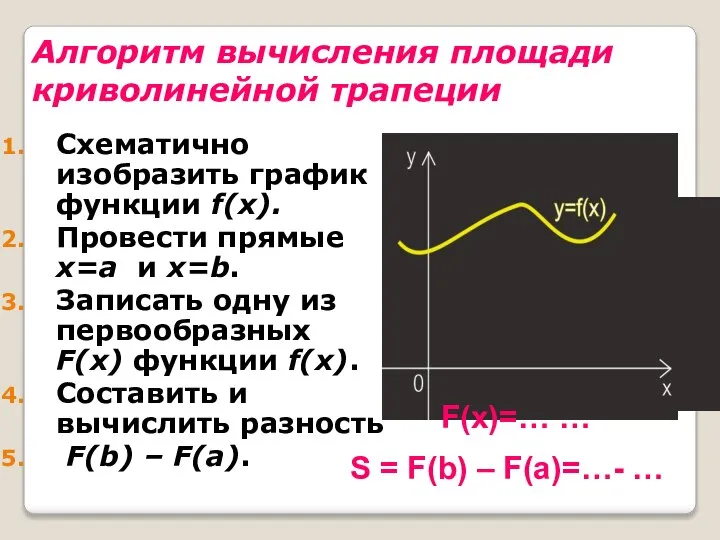
- 40. Алгоритм вычисления площади криволинейной трапеции Схематично изобразить график функции f(x). Провести прямые x=a и x=b. Записать
- 41. Вычислить площадь фигуры, ограниченной линиями, используя формулу Ньютона-Лейбница Вариант 1 f(x) = 2x – 3 y
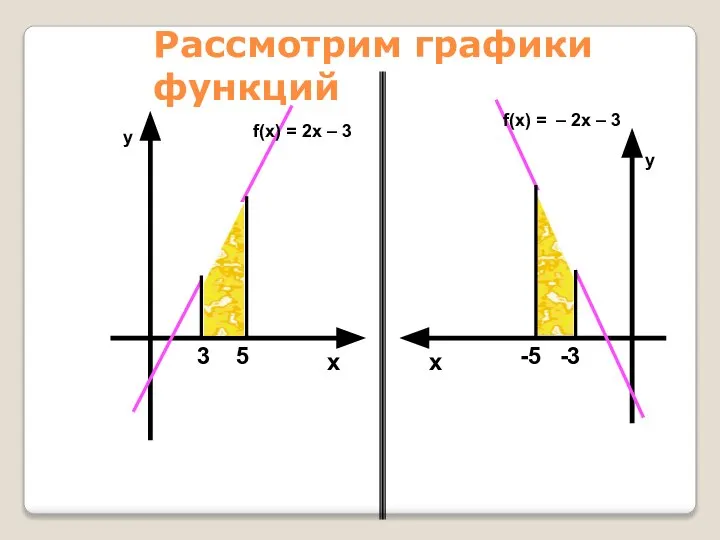
- 42. Рассмотрим графики функций f(x) = 2x – 3 f(x) = – 2x – 3 у у
- 43. Проверим решение Если f(x) = 2x – 3 Вариант 1.
- 44. Проверим решение Если f(x) = – 2x – 3 Вариант 2.
- 45. Вычисление площади плоских фигур с помощью определенного интеграла Площадь фигуры (S), ограниченной прямыми х = а
- 46. Например: Вычислить площадь фигуры, ограниченной графиками функций
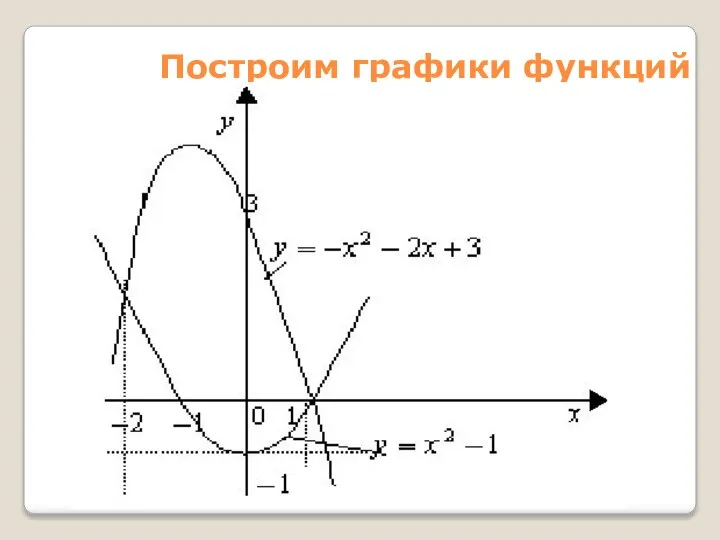
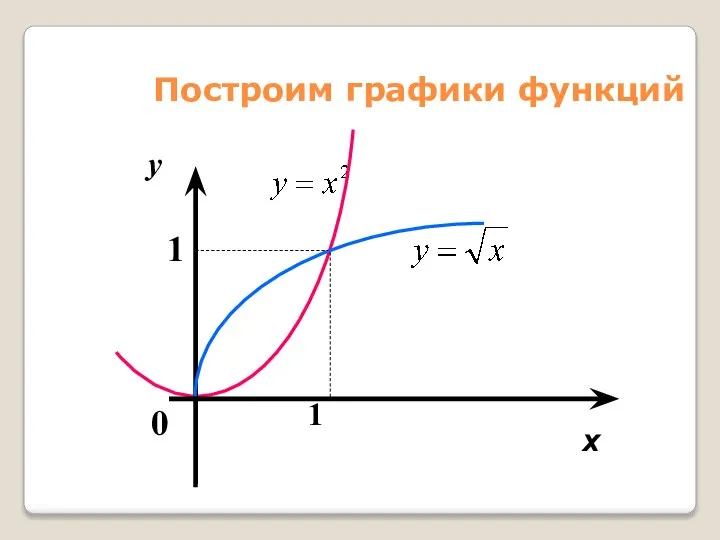
- 47. Построим графики функций
- 48. Значит Пределы интегрирования: от-2 до1 f(x)= - x²-2x+3 g(x)=x² - 1 Тогда =
- 49. =
- 50. Запомним Геометрический смысл определенного интеграла – это площадь криволинейной трапеции Физический смысл определенного интеграла – это…
- 51. Вычисление объема тела вращения Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой у
- 52. Например Найти объем тела, полученного вращением вокруг оси Ox криволинейных трапеций, ограниченных линиями у= х² и
- 53. Построим графики функций х
- 54. Решение Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox криволинейных трапеций, ограниченных
- 55. =
- 56. Применение интеграла Площадь фигуры Объем тела вращения Работа электрического заряда Работа переменной силы Масса Перемещение Дифференциальное
- 58. Скачать презентацию



























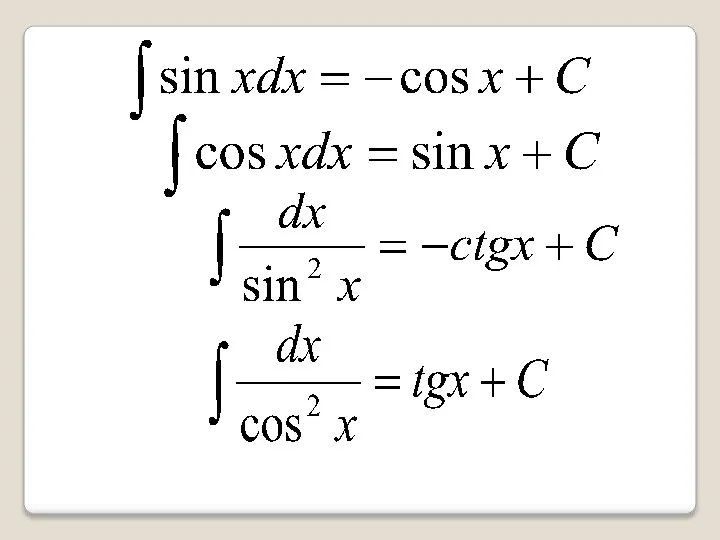



![Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и пусть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/918768/slide-34.jpg)
![Формула Ньютона-Лейбница Теорема: если функция у = f(x) непрерывна на отрезке [а;в],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/918768/slide-36.jpg)








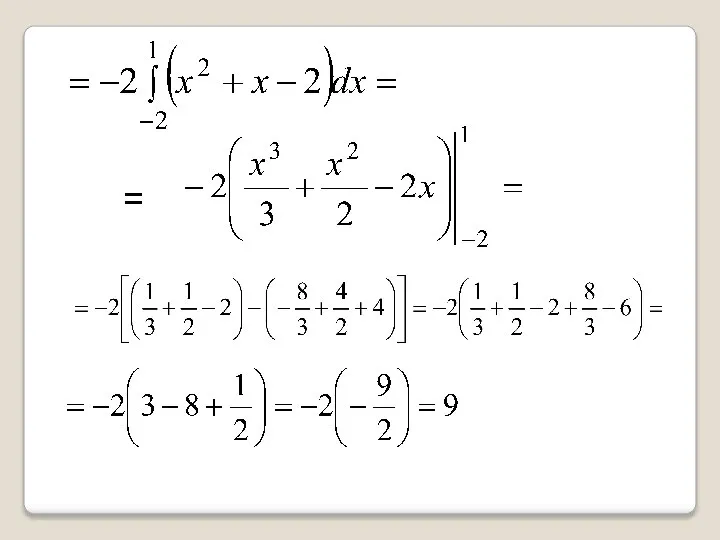




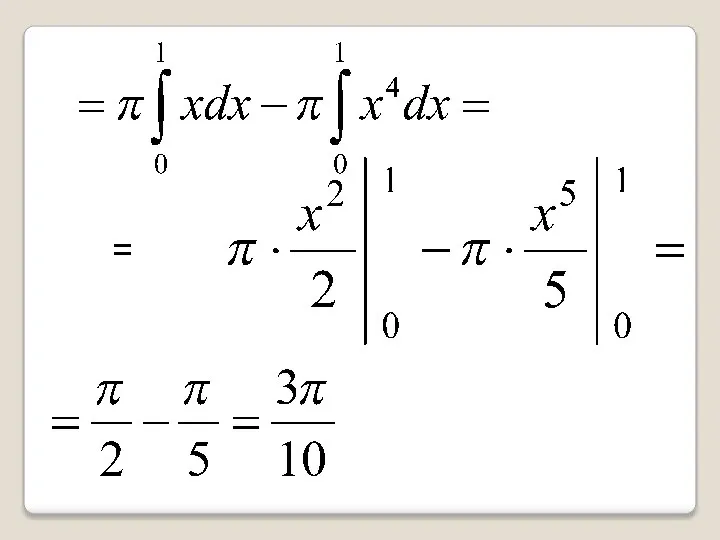

 Теорема Пифагора
Теорема Пифагора Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Плоскость касательной к сфере
Плоскость касательной к сфере Сложение и вычитание векторов. Демонстрационный материал. 9 класс
Сложение и вычитание векторов. Демонстрационный материал. 9 класс Презентация на тему Равнобедренная трапеция
Презентация на тему Равнобедренная трапеция  Оболочки отрицательной Гаусовой кривизны
Оболочки отрицательной Гаусовой кривизны Тест по теме Векторы в пространстве. 11 класс
Тест по теме Векторы в пространстве. 11 класс Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Свойства линейной функции и графическое изображение механического движения
Свойства линейной функции и графическое изображение механического движения Числа, кратные 3
Числа, кратные 3 Теория вероятностей и математическая статистика (Лекция 7)
Теория вероятностей и математическая статистика (Лекция 7) Площадь фигур - какие они
Площадь фигур - какие они Задачи на построение
Задачи на построение Решаем задачи
Решаем задачи Геометрия вокруг нас
Геометрия вокруг нас 11г 12.09
11г 12.09 Число или цифра 2
Число или цифра 2 Конус. Площадь поверхности конуса
Конус. Площадь поверхности конуса Ну, погоди!
Ну, погоди! Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника
Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника Очень жадный крокодил или больше, меньше, равно
Очень жадный крокодил или больше, меньше, равно Табличные случаи сложения и вычитания с переходом через разряд в пределах 20
Табличные случаи сложения и вычитания с переходом через разряд в пределах 20 Презентация на тему Скрещивающиеся прямые
Презентация на тему Скрещивающиеся прямые  Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Задания по математике (5 класс, часть 3)
Задания по математике (5 класс, часть 3) Числовые ряды
Числовые ряды Тест № 2 по теме Функция
Тест № 2 по теме Функция Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками
Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками