Содержание
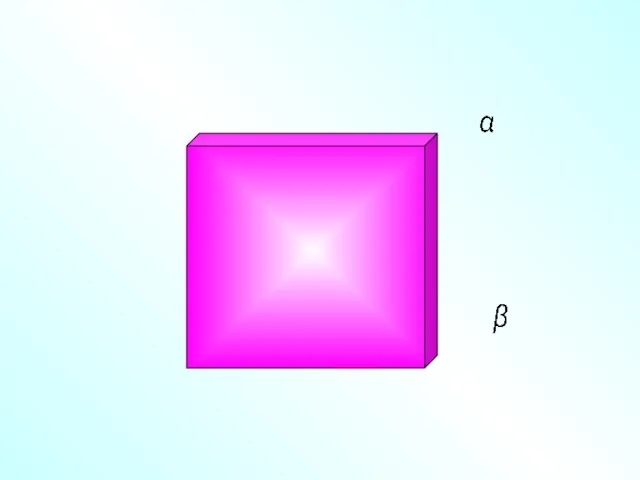
- 2. Расположение плоскостей в пространстве. α ∩ β α и β совпадают α ⎜⎜ β
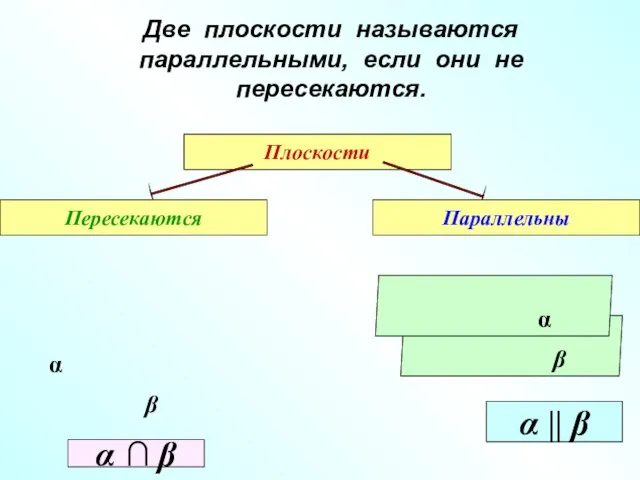
- 3. Две плоскости называются параллельными, если они не пересекаются. Плоскости Пересекаются Параллельны β α α || β
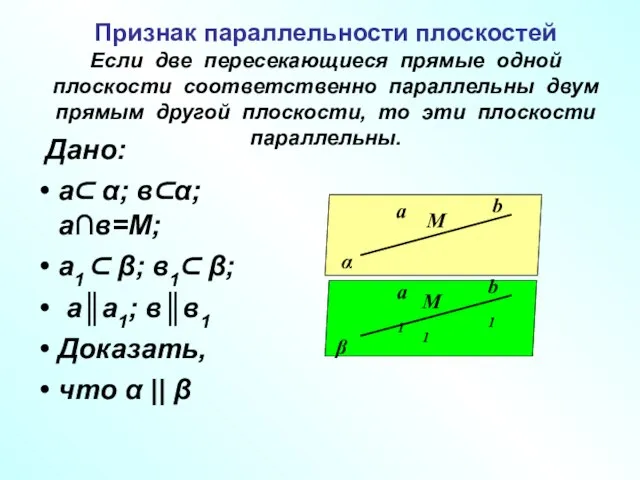
- 6. Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то
- 7. Доказательство от противного α β а b М b1 а1 М1 с а ⊂α; а1⊂ β;
- 8. Какие теоремы мы использовали при доказательстве признака?
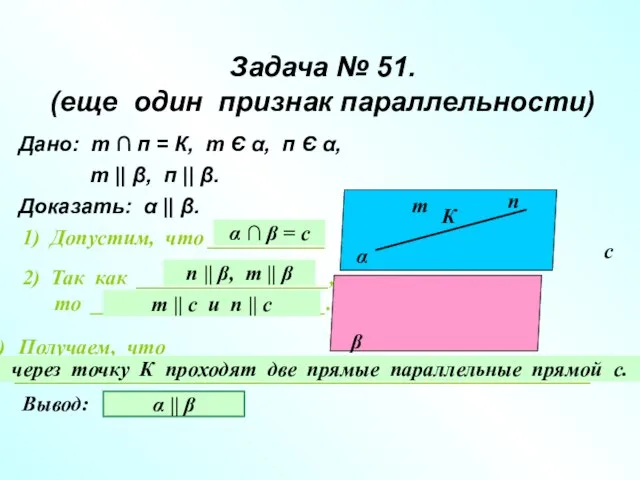
- 9. Задача № 51. (еще один признак параллельности) Дано: т ∩ п = К, т Є α,
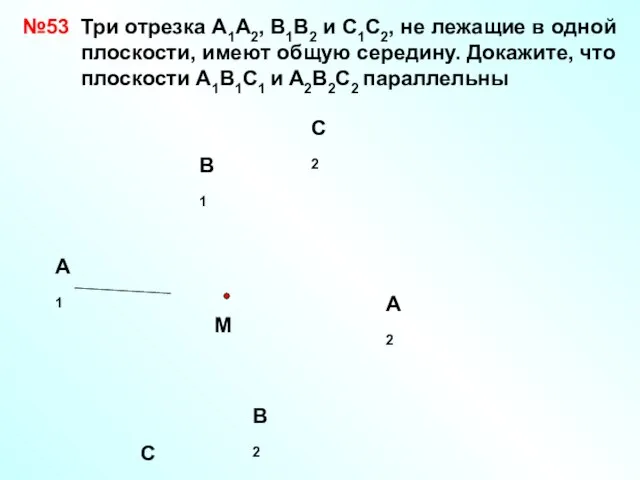
- 10. Задача № 53. Дано: отрезки А1А2, В1В2, С1С2 не лежат в одной плоскости и имеет общую
- 11. Отвечаем на вопросы Могут ли прямая и плоскость не иметь общих точек? Верно ли, что если
- 12. Проверяем свою работу Могут ли прямая и плоскость не иметь общих точек? Да Верно ли, что
- 13. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Свойства параллельных плоскостей. Дано: α
- 14. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Свойства параллельных плоскостей. Доказать: АВ = СD Дано:
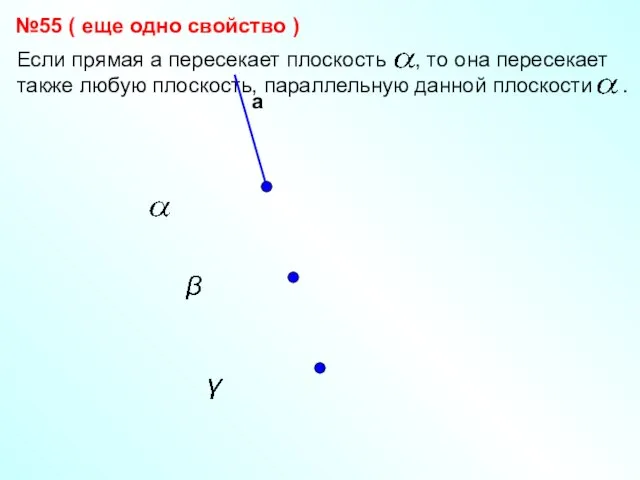
- 15. №55 ( еще одно свойство )
- 16. Решение задачи № 58.(еще одно свойство) Доказать: β пересекается с γ Дано: α ⎜⎜ β, α
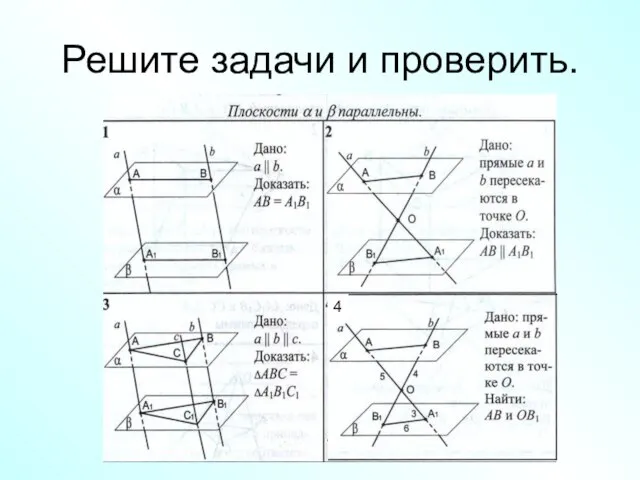
- 17. Решите задачи и проверить.
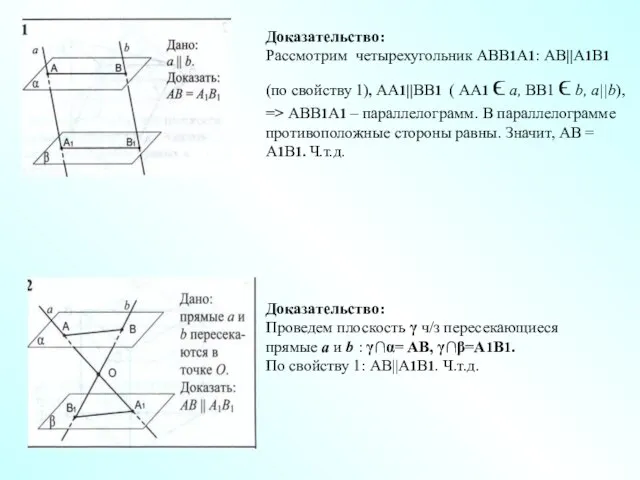
- 18. Доказательство: Рассмотрим четырехугольник АВВ1А1: АВ||А1В1 (по свойству 1), АА1||ВВ1 ( АА1 ϵ а, ВВ1 ϵ b,
- 19. 4 Доказательство: По свойствам 1 и 2 четырехугольники АСС1А1, ВСС1В1, АВВ1А1 – параллелограммы. В параллелограмме противоположные
- 20. №60 Если две плоскости и параллельны плоскости , то плоскости и параллельны. Признак параллельности трех плоскостей
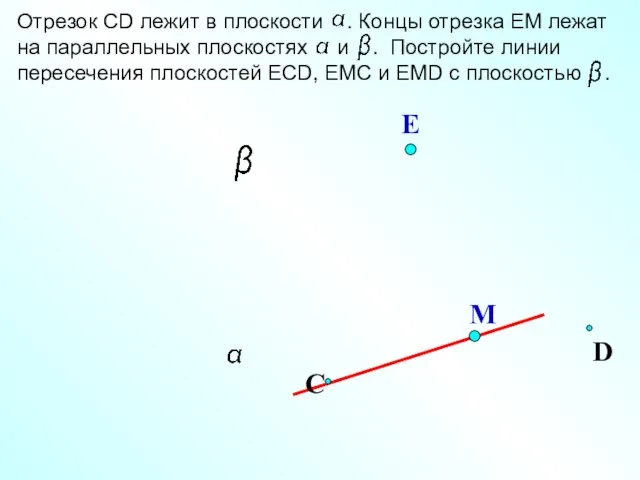
- 21. D Е М С
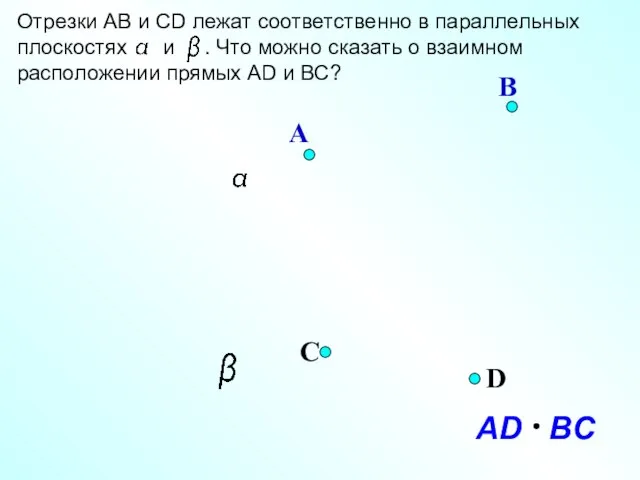
- 22. D А Концы отрезков АВ и СD лежат на параллельных плоскостях и . Постройте линии пересечения
- 23. D А В С
- 24. Плоскости и параллельны, прямые a и b пересекаются в точке М. Прямая a пересекает плоскости и
- 25. a a1 A A1 B
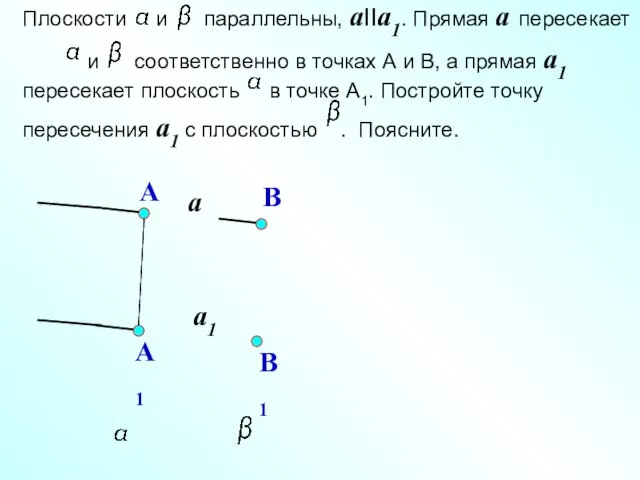
- 26. Плоскости и параллельны, прямая a пересекает плоскости и соответственно в точках А и В, а прямая
- 27. Плоскости и параллельны. Пересекающиеся в точке М прямые a и b пересекают плоскость соответственно в точках
- 28. А1 В1 С1 А2 С2 В2 №53 М Три отрезка А1А2, В1В2 и С1С2, не лежащие
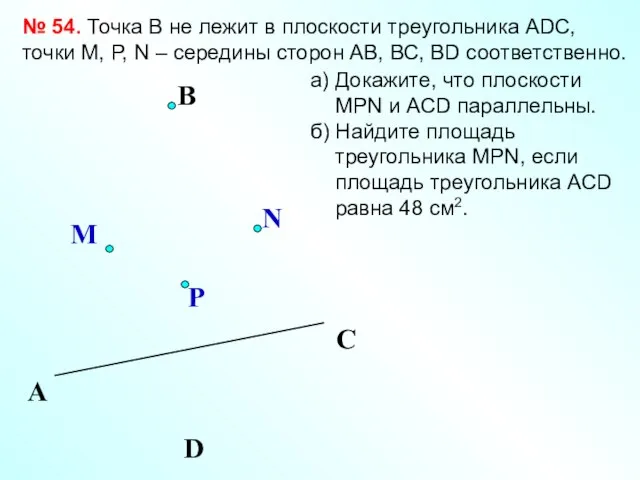
- 29. A D C № 54. Точка В не лежит в плоскости треугольника АDC, точки М, P,
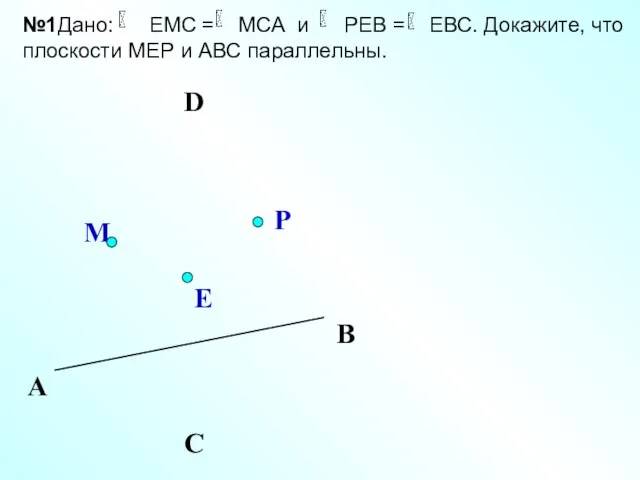
- 30. D Е М Р А С В №1Дано: ЕМС = МСА и РЕВ = ЕВС. Докажите,
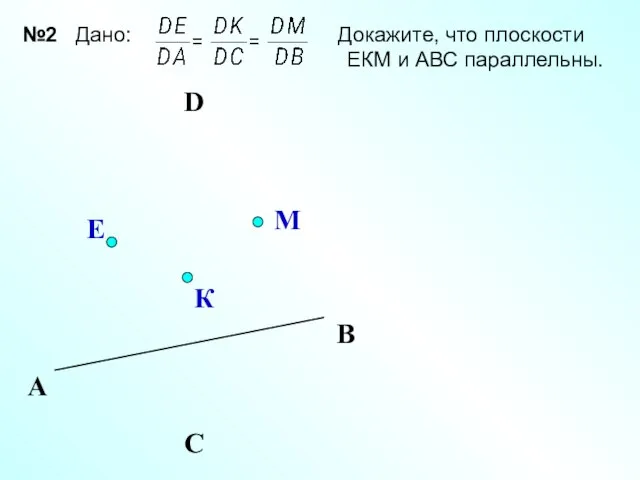
- 31. D К Е М А С В №2 Дано: Докажите, что плоскости ЕКМ и АВС параллельны.
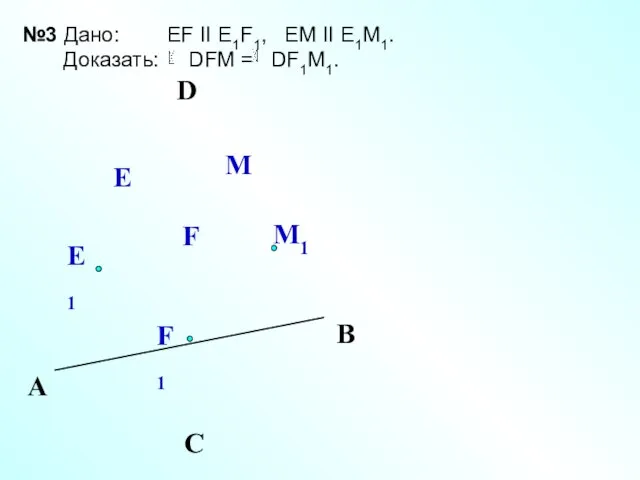
- 32. Е М1 А С В №3 Дано: EF II E1F1, EM II E1M1. Доказать: DFM =
- 33. C1 a b №4 Дано: a II b II c и не лежат в одной плоскости,
- 35. Скачать презентацию

















 Презентация на тему Прямоугольная система координат в пространстве (11 класс)
Презентация на тему Прямоугольная система координат в пространстве (11 класс)  Задачи на построение (геометрия, 7 класс)
Задачи на построение (геометрия, 7 класс) Решение показательных уравнений
Решение показательных уравнений Теорема Пифагора
Теорема Пифагора Теорема о площади треугольника
Теорема о площади треугольника Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)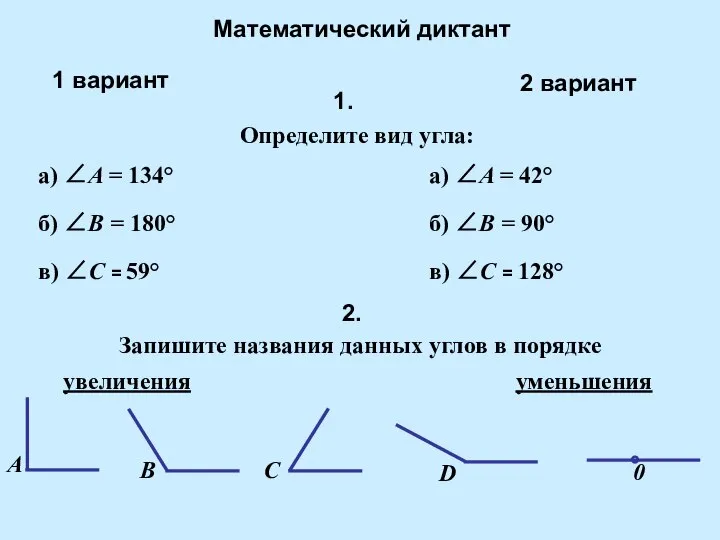 Математический диктант
Математический диктант Среднее арифметическое
Среднее арифметическое Арифметический пейзаж
Арифметический пейзаж Задачи на концентрацию
Задачи на концентрацию Подготовка к ГИА. Задания
Подготовка к ГИА. Задания Тригонометрия. ЕГЭ, задание 7
Тригонометрия. ЕГЭ, задание 7 Геометрические фигуры
Геометрические фигуры Презентация на тему Измеряем длину окружности
Презентация на тему Измеряем длину окружности  Куб. Формулы для куба
Куб. Формулы для куба Виды четырехугольников
Виды четырехугольников Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ  Задачи на увеличение числа в несколько раз
Задачи на увеличение числа в несколько раз Проверка вычитания
Проверка вычитания Цилиндр
Цилиндр Задания по геометрии
Задания по геометрии Повторение изученного. 1 класс
Повторение изученного. 1 класс Презентация на тему Миллиметр (2 класс)
Презентация на тему Миллиметр (2 класс)  Иррациональные уравнения и их системы. Иррациональные неравенства
Иррациональные уравнения и их системы. Иррациональные неравенства Натуральные числа (5 класс)
Натуральные числа (5 класс) Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Смешанные числа
Смешанные числа Космическая игра. Таблица умножения
Космическая игра. Таблица умножения