Содержание
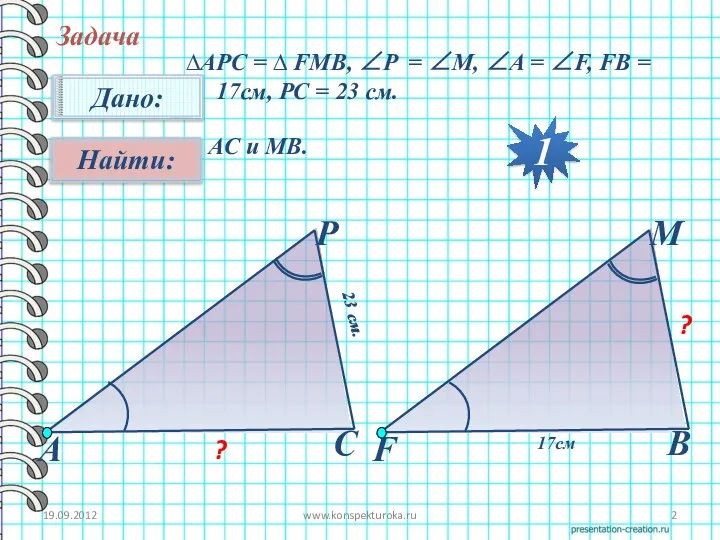
- 2. 19.09.2012 www.konspekturoka.ru Задача ∆АPC = ∆ FMB, ∠P = ∠M, ∠A = ∠F, FB = 17см,
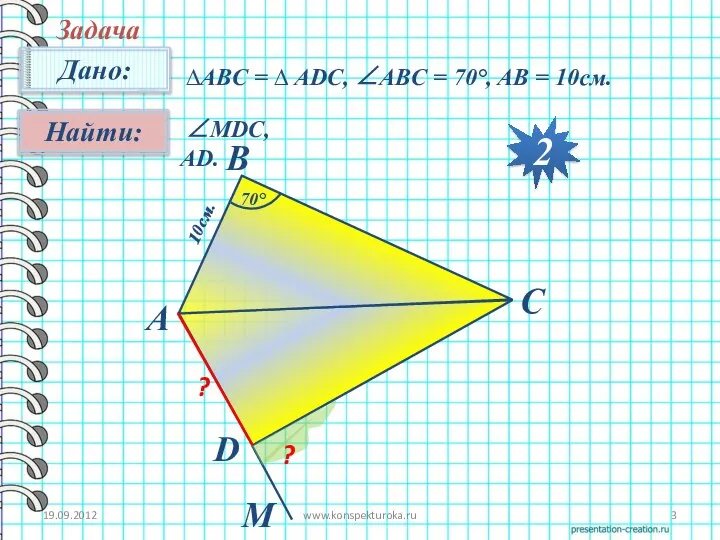
- 3. 19.09.2012 www.konspekturoka.ru Задача ∆АВC = ∆ ADC, ∠ABC = 70°, AB = 10см. 2 ∠MDC, AD.
- 4. 19.09.2012 www.konspekturoka.ru Какие условия должны выполняться для того чтобы ∆ АВС = ∆ MNK? стороны и
- 5. 19.09.2012 www.konspekturoka.ru Не нужно проверять равенство всех сторон и углов! Достаточно сравнить лишь три элемента одного
- 6. 19.09.2012 www.konspekturoka.ru Доказывать признаки нужно с помощью теоремы. Теорема - утверждение, справедливость которого устанавливается путем рассуждений).
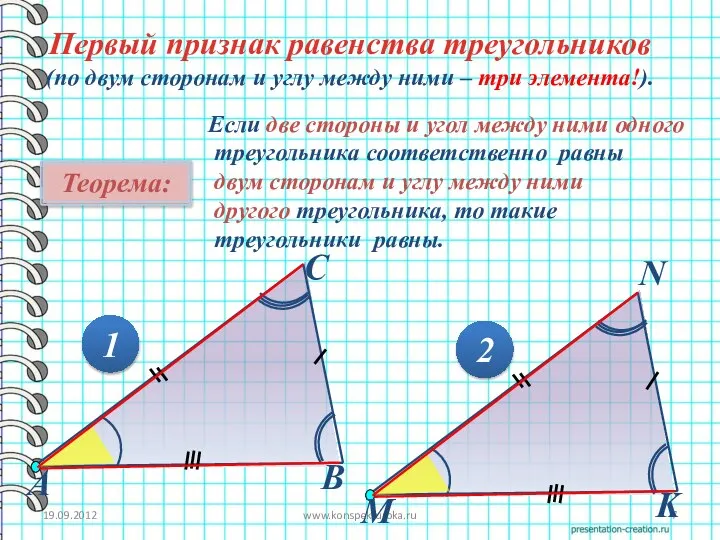
- 7. 19.09.2012 www.konspekturoka.ru Первый признак равенства треугольников (по двум сторонам и углу между ними – три элемента!).
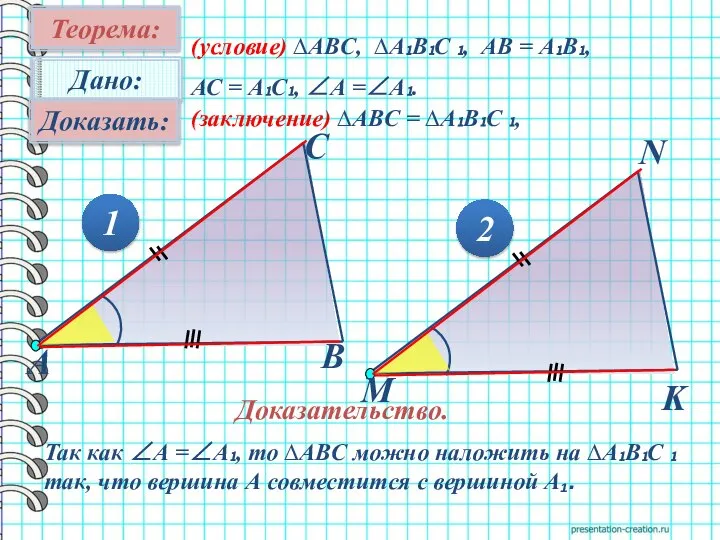
- 8. Теорема: 1 2 (условие) ∆АВC, ∆А₁В₁С ₁, АВ = А₁В₁, АС = А₁С₁, ∠А =∠А₁. (заключение)
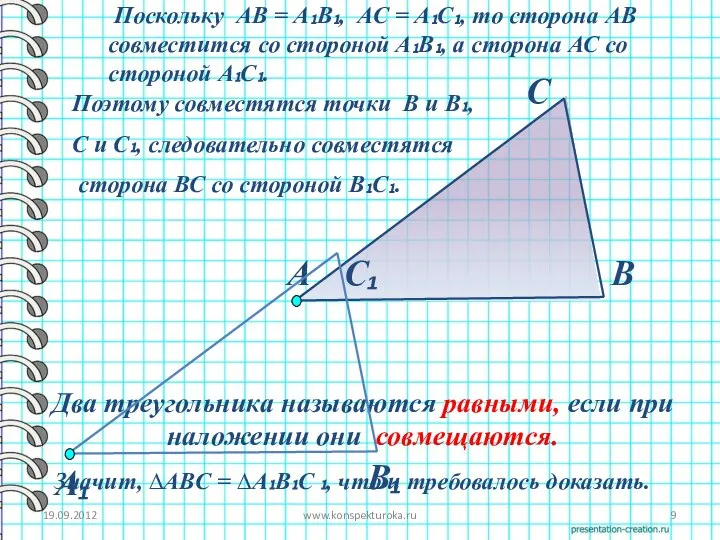
- 9. 19.09.2012 www.konspekturoka.ru Два треугольника называются равными, если при наложении они совмещаются. А В С Поскольку АВ
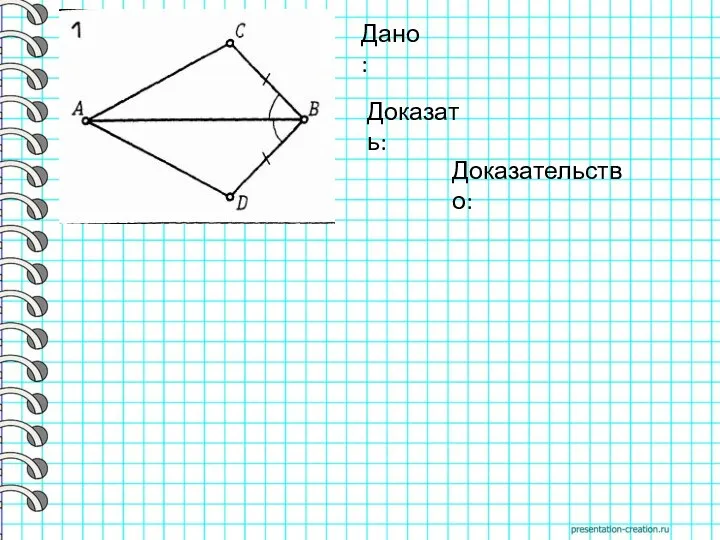
- 10. Дано: Доказать: Доказательство:
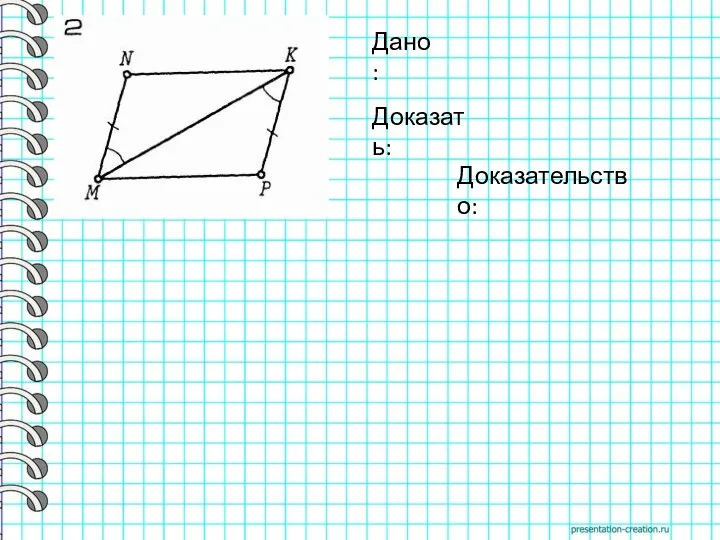
- 11. Дано: Доказать: Доказательство:
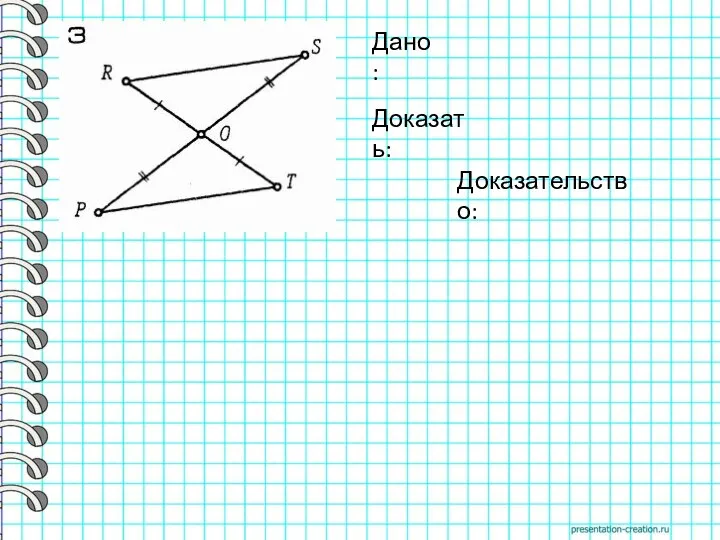
- 12. Дано: Доказать: Доказательство:
- 14. Скачать презентацию



 Использование современных программных комплексов в расчете строительных конструкций. Внешние силы. Объемные силы
Использование современных программных комплексов в расчете строительных конструкций. Внешние силы. Объемные силы Логарифмы
Логарифмы Памятки по математике
Памятки по математике Сложная функция. Производная сложной функции
Сложная функция. Производная сложной функции Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Погрешности измерений
Погрешности измерений Умножение дробей
Умножение дробей Устные и письменные приемы вычислений
Устные и письменные приемы вычислений Сравнение по длине
Сравнение по длине Деление окружности на равные части
Деление окружности на равные части Пирамида. Элементы пирамиды. Поверхность пирамиды
Пирамида. Элементы пирамиды. Поверхность пирамиды Понятие многогранник, призма
Понятие многогранник, призма Параллельность плоскостей определение
Параллельность плоскостей определение Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Проекции вектора на оси координат
Проекции вектора на оси координат Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Десятичные дроби в разных профессиях. 6 класс
Десятичные дроби в разных профессиях. 6 класс Rinjka liinija
Rinjka liinija Симметрия
Симметрия Интегралы. Неопределенный интеграл
Интегралы. Неопределенный интеграл Действия с десятичными дробями 5 класс
Действия с десятичными дробями 5 класс Средства измерений, классификация. Метрологические характеристики средств измерений
Средства измерений, классификация. Метрологические характеристики средств измерений Общие уравнения прямой. Уравнение (формула)
Общие уравнения прямой. Уравнение (формула) Разложение на простые множители
Разложение на простые множители Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Сечения в геометрии
Сечения в геометрии Прямоугольные треугольники
Прямоугольные треугольники Презентация. Ромб. Квадрат
Презентация. Ромб. Квадрат