Содержание
- 2. Пусть задан график функции y = f(x) Преобразование вида y = kf(x) Преобразование вида y =
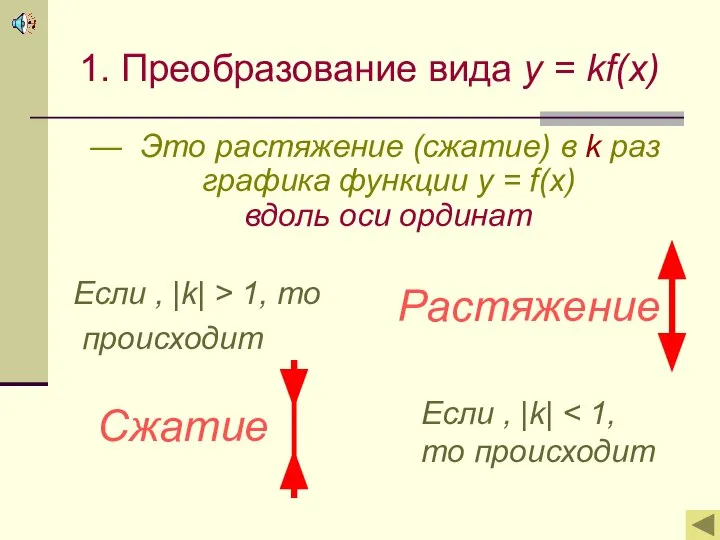
- 3. 1. Преобразование вида y = kf(x) — Это растяжение (сжатие) в k раз графика функции y
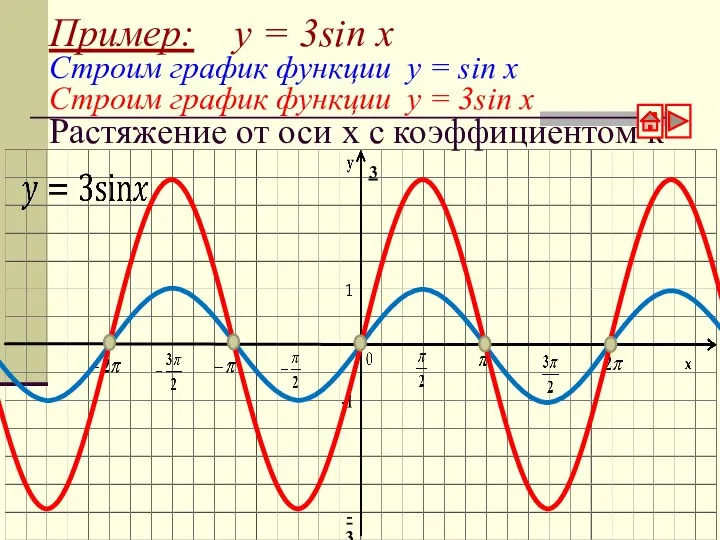
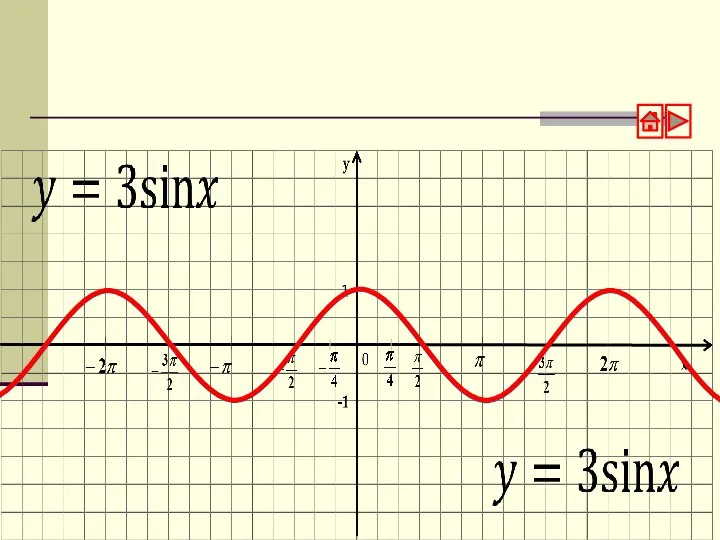
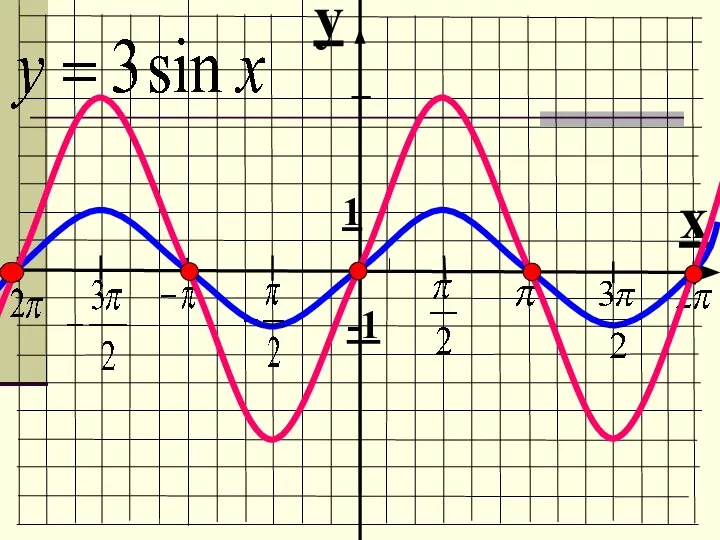
- 4. Пример: y = 3sin x Строим график функции у = sin x Строим график функции у
- 6. 2.Для построения графика функции y=-f(x) необходимо график функции y=f(x)симметрично отобразить относительно оси ОХ
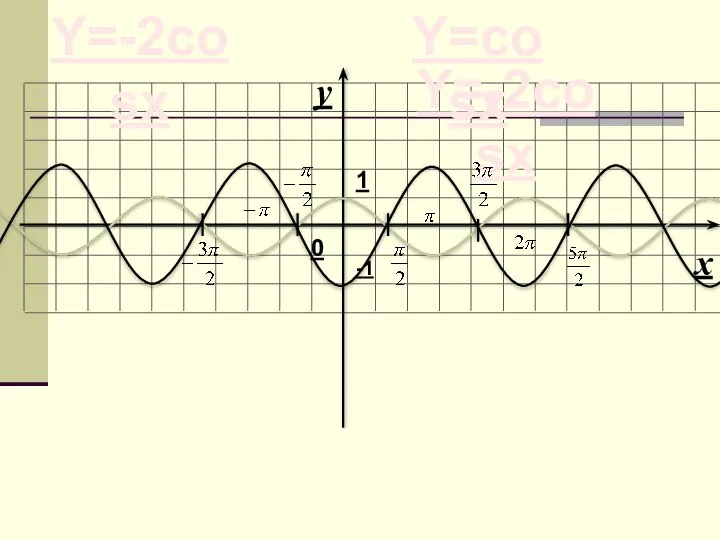
- 7. Y=cosx Y=-2cosx -1 Y=-2cosx
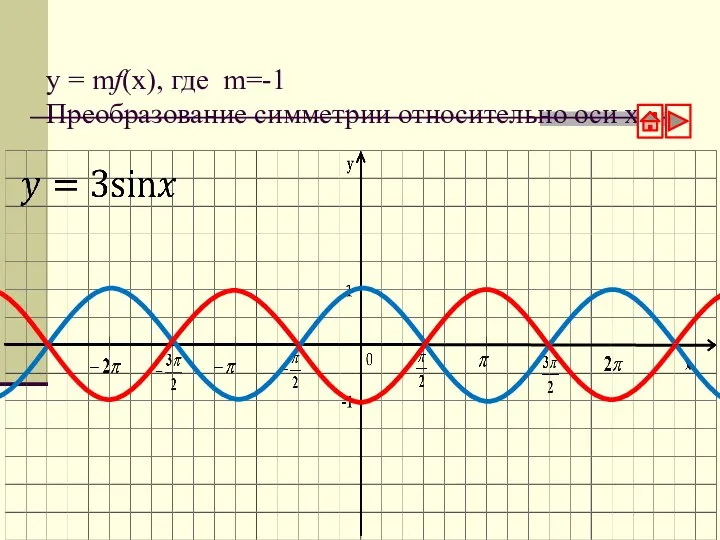
- 8. y = mf(x), где m=-1 Преобразование симметрии относительно оси х
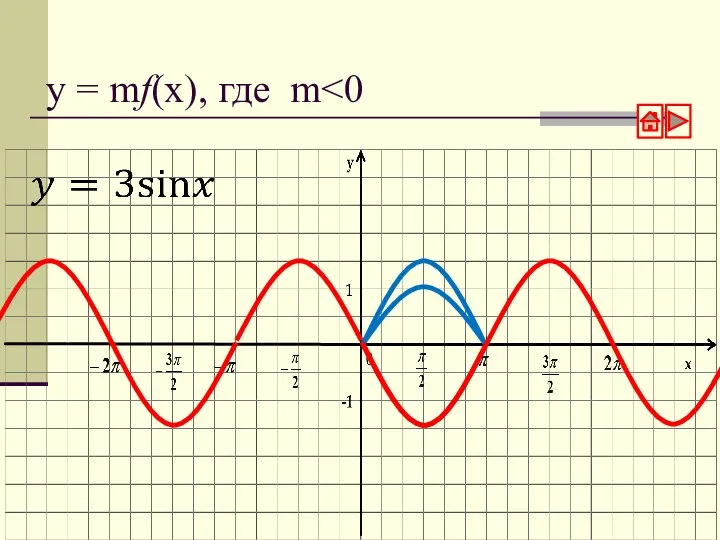
- 9. y = mf(x), где m
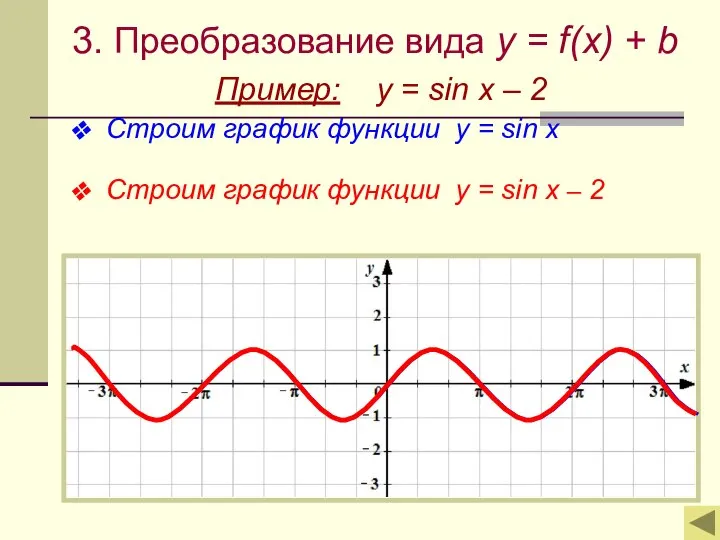
- 10. 3. Преобразование вида y = f(x) + b — Это параллельный перенос графика функции y =
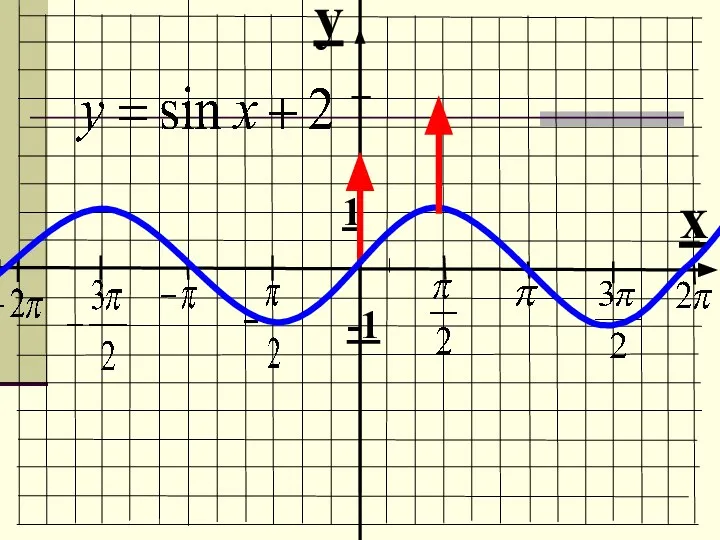
- 11. 3. Преобразование вида y = f(x) + b Пример: y = sin x – 2 Строим
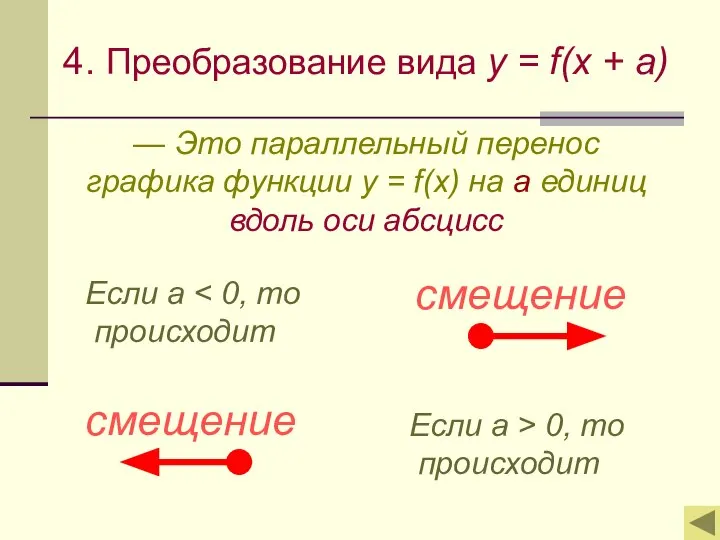
- 12. 4. Преобразование вида y = f(x + a) — Это параллельный перенос графика функции y =
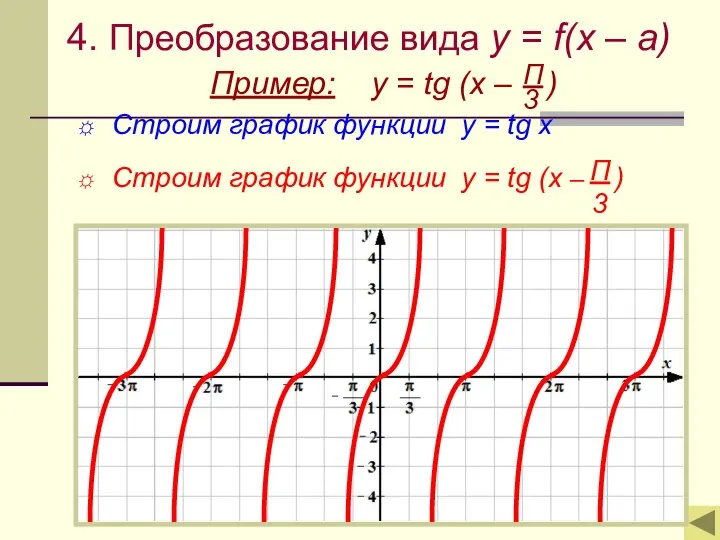
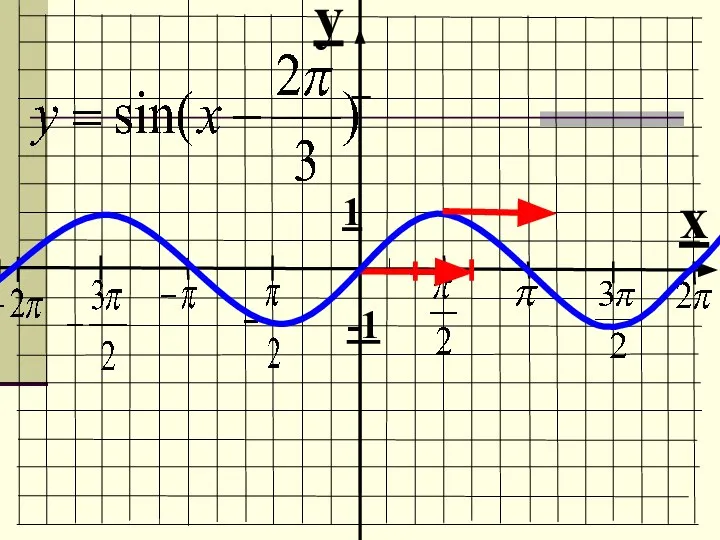
- 13. 4. Преобразование вида y = f(x – a) Пример: y = tg (x – ) Строим
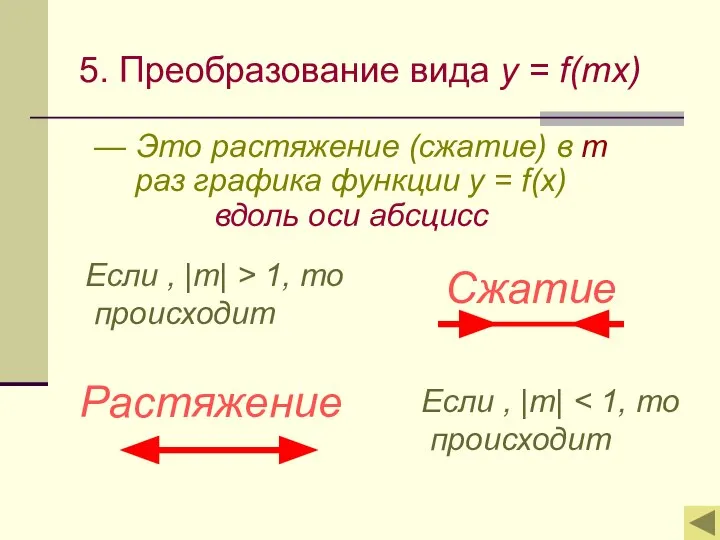
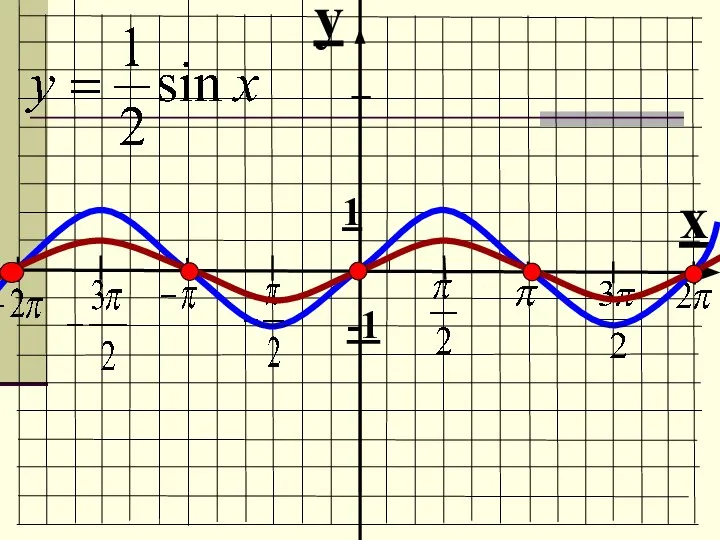
- 15. 5. Преобразование вида y = f(mx) — Это растяжение (сжатие) в m раз графика функции y
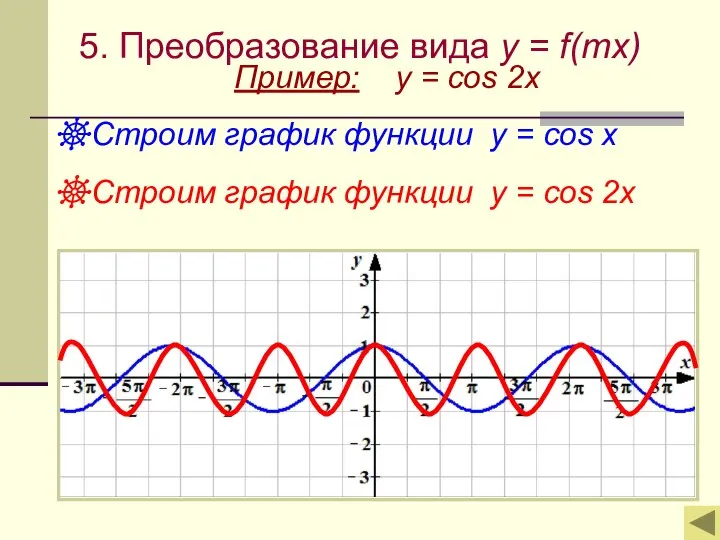
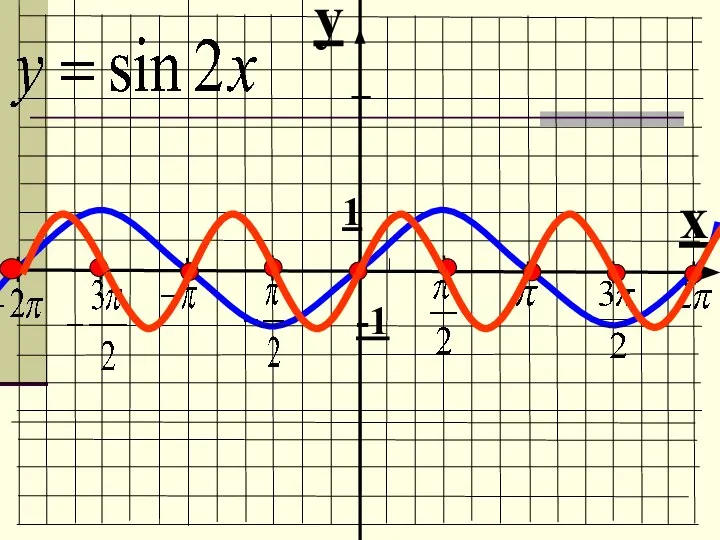
- 16. 5. Преобразование вида y = f(mx) Пример: y = cos 2x Строим график функции у =
- 17. 6. Преобразование вида y = |f(x)| — Это отображение нижней части графика функции y = f(x)
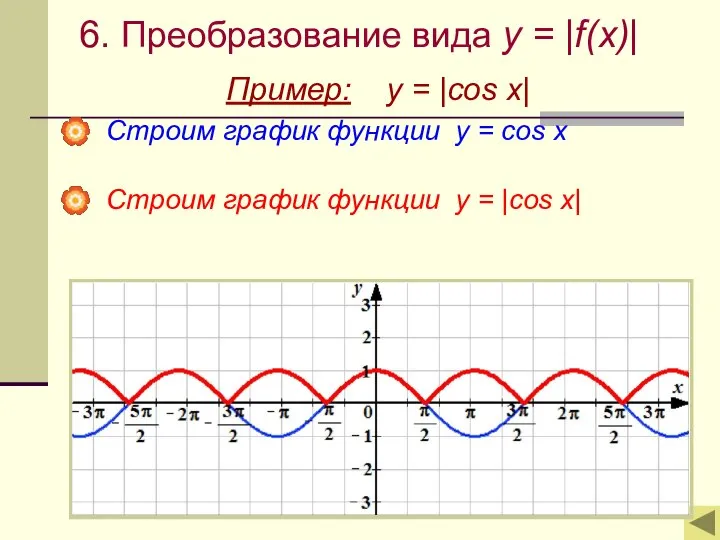
- 18. 6. Преобразование вида y = |f(x)| Пример: y = |cos x| Строим график функции у =
- 19. 7. Преобразование вида y = f (|x|) — Это отображение правой части графика функции y =
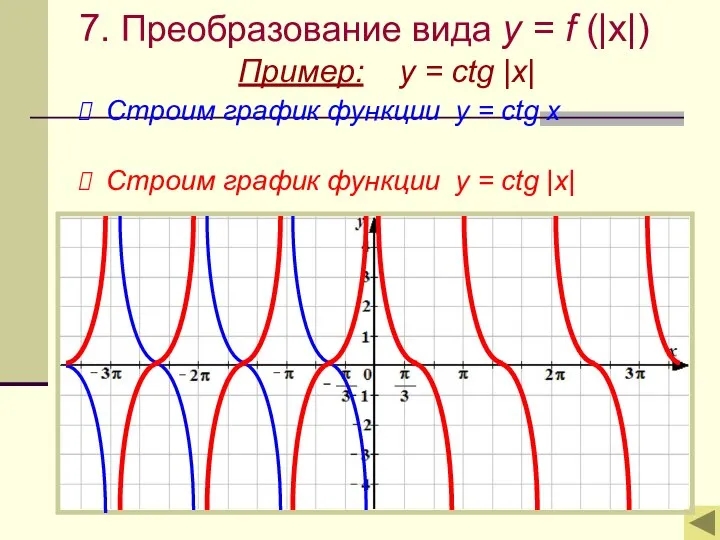
- 20. 7. Преобразование вида y = f (|x|) Пример: y = ctg |x| Строим график функции у
- 21. Составь алгоритм построения графиков
- 23. y x 1 -1
- 25. y x 1 -1
- 27. y x 1 -1
- 29. y x 1 -1
- 31. y x 1 -1
- 34. Скачать презентацию







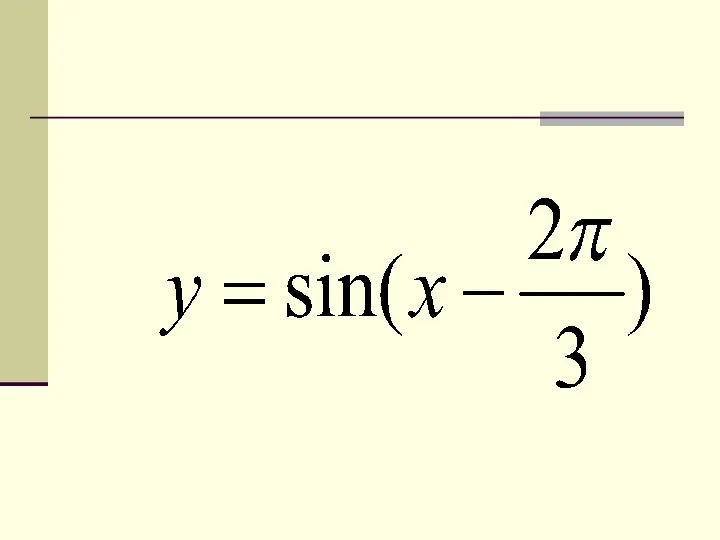
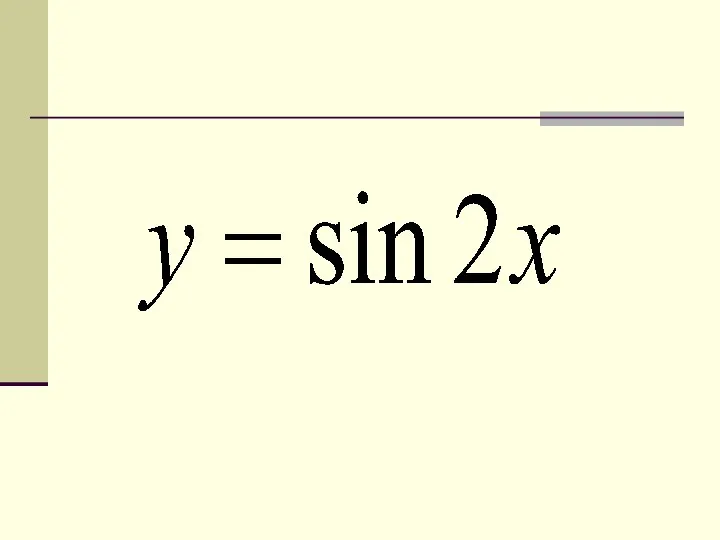
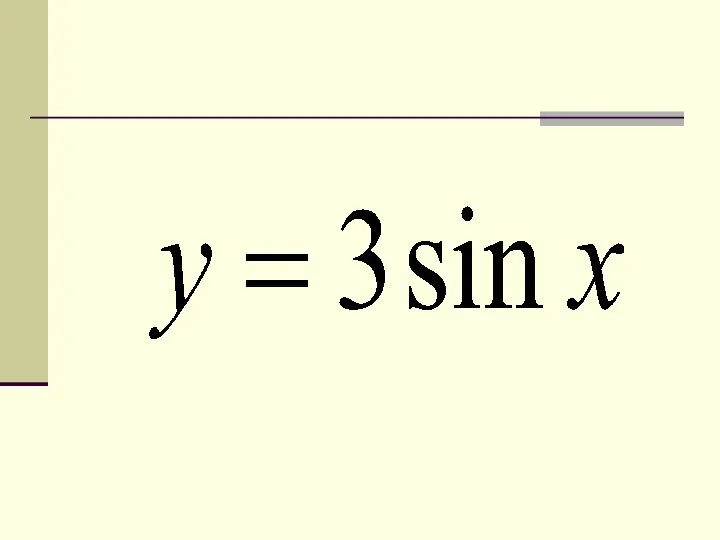
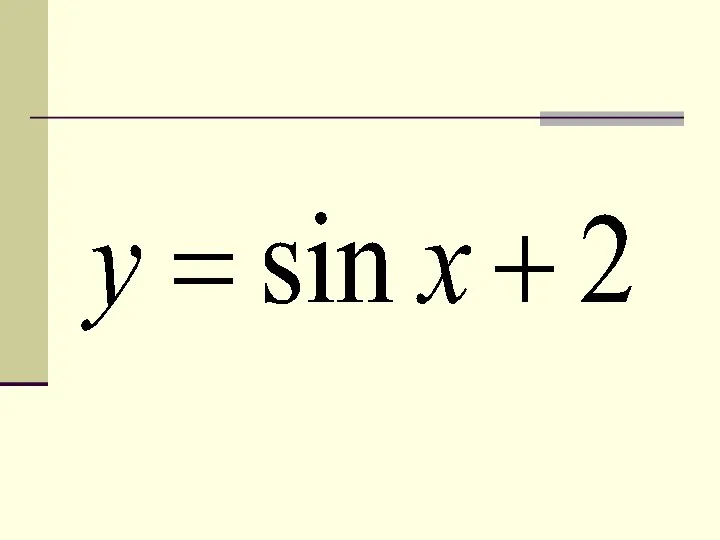
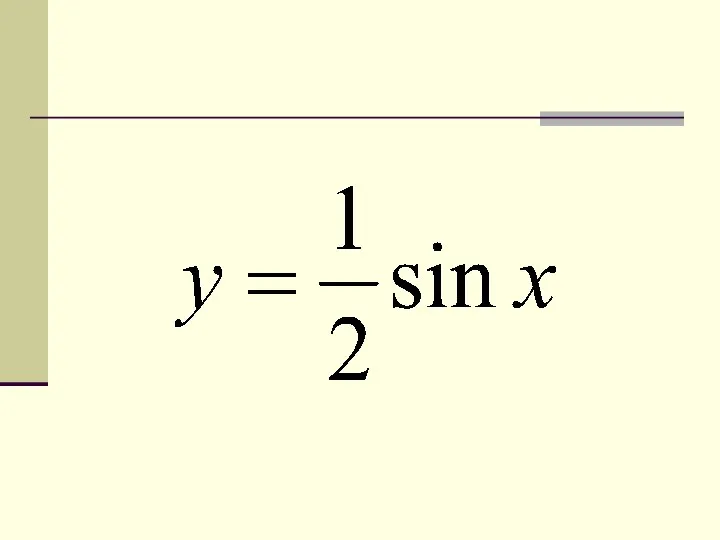
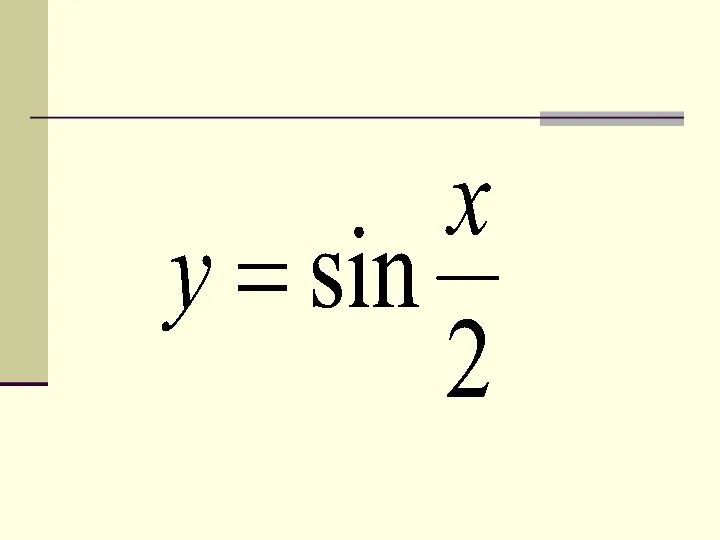
 Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Поліноми. Додавання поліномів
Поліноми. Додавання поліномів Решение задач
Решение задач Характеристическое свойство арифметической прогрессии
Характеристическое свойство арифметической прогрессии Параллелепипед. Виды параллелепипедов
Параллелепипед. Виды параллелепипедов Отрицательная степень числа. Контрольная работа
Отрицательная степень числа. Контрольная работа Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Взаимное расположение прямых и плоскостей
Взаимное расположение прямых и плоскостей Тригонометрически уравнения
Тригонометрически уравнения Лекция_04
Лекция_04 Что такое разложение на множители и зачем оно нужно
Что такое разложение на множители и зачем оно нужно Сумма углов треугольника
Сумма углов треугольника Решение иррациональных неравенств
Решение иррациональных неравенств Логарифм числа и его свойства
Логарифм числа и его свойства Сколько останется? Посчитай и назови ответ
Сколько останется? Посчитай и назови ответ Интегральное исчисление. Первообразная функция. Неопределённый интеграл. Методы интегрирования. Определенный интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл. Методы интегрирования. Определенный интеграл Презентация на тему Числовые и буквенные выражения (5 класс)
Презентация на тему Числовые и буквенные выражения (5 класс)  Кривые второго порядка
Кривые второго порядка Конструктивные объекты
Конструктивные объекты Задачи, обратные данной
Задачи, обратные данной Сложение вида +2, +3
Сложение вида +2, +3 З історії геометрії
З історії геометрії Декартова система координат
Декартова система координат Деление с остатком
Деление с остатком Виды углов.Измерение углов
Виды углов.Измерение углов Математика. Реши примеры
Математика. Реши примеры Бинарные отношения
Бинарные отношения Презентация на тему Одночлен
Презентация на тему Одночлен