Содержание
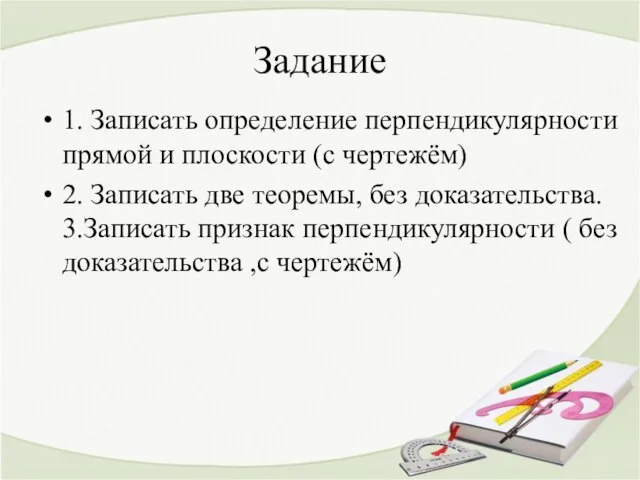
- 2. Задание 1. Записать определение перпендикулярности прямой и плоскости (с чертежём) 2. Записать две теоремы, без доказательства.
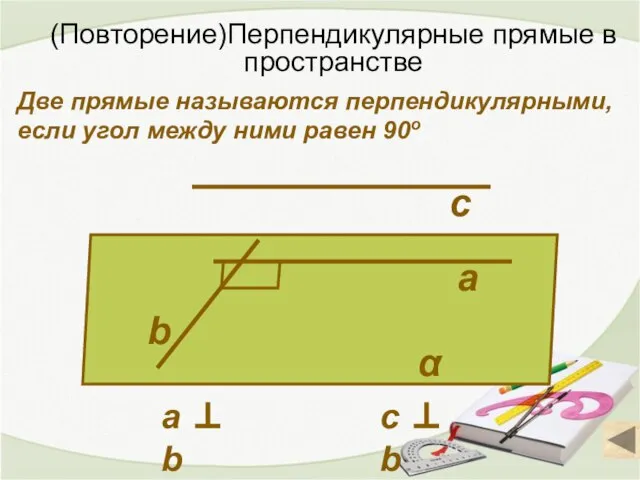
- 3. (Повторение)Перпендикулярные прямые в пространстве Две прямые называются перпендикулярными, если угол между ними равен 90о а b
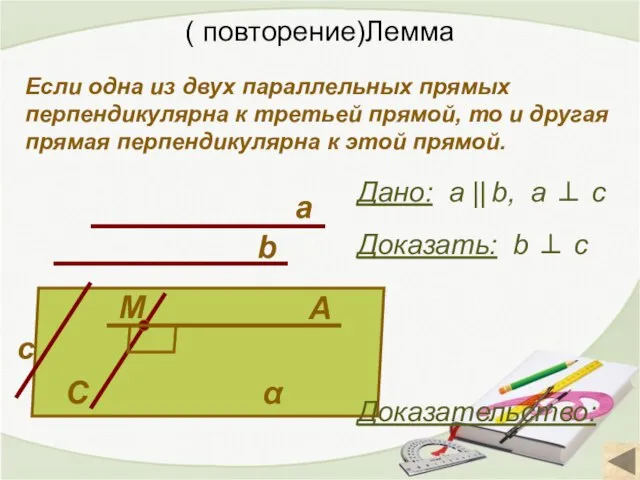
- 4. ( повторение)Лемма Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая
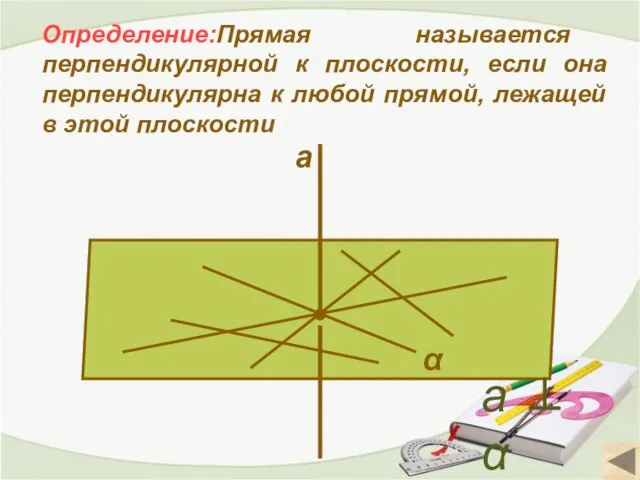
- 5. Определение:Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости α
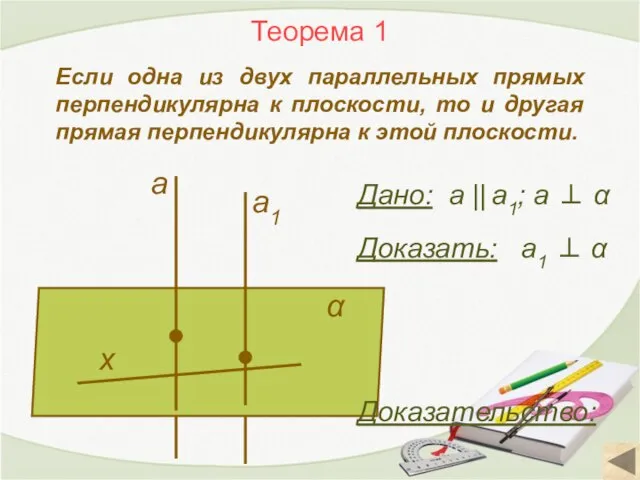
- 6. Теорема 1 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна
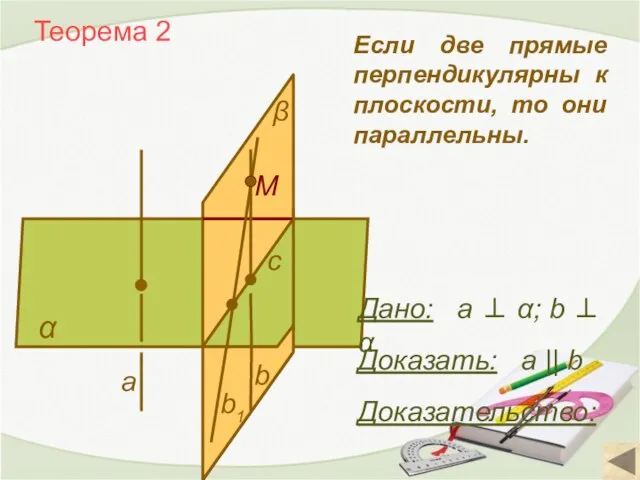
- 7. Теорема 2 α Доказать: а || b Доказательство: Если две прямые перпендикулярны к плоскости, то они
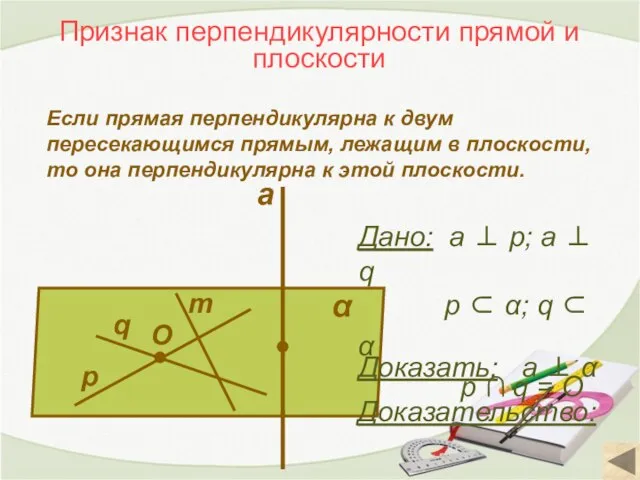
- 8. Признак перпендикулярности прямой и плоскости Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то
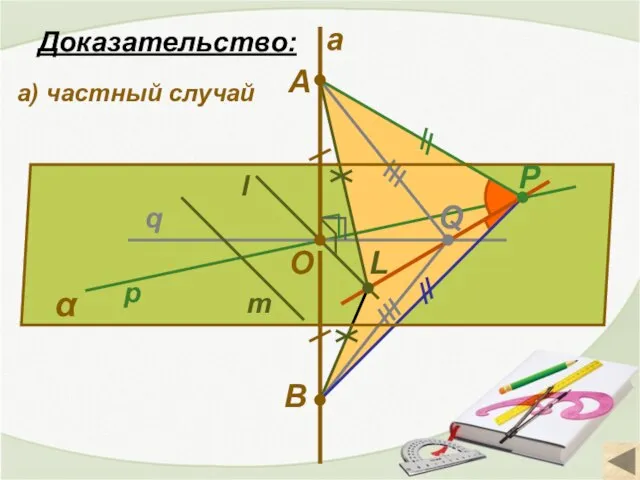
- 9. α q l m O a p B P Q Доказательство: L а) частный случай A
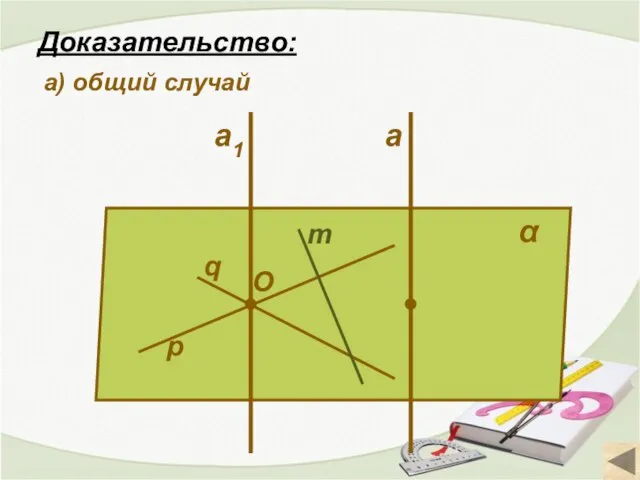
- 10. α q a p m O Доказательство: а) общий случай a1
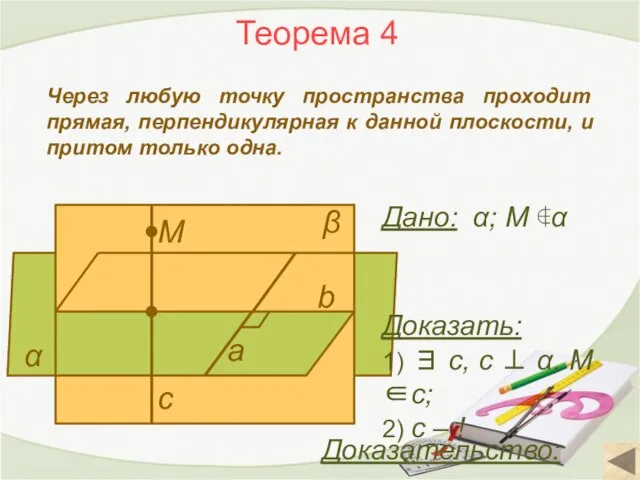
- 11. Теорема 4 Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
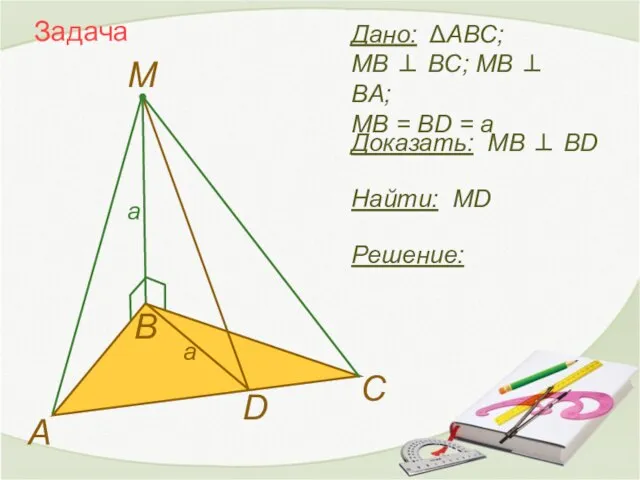
- 12. Задача Найти: MD А В D M Решение: Дано: ΔABC; MB ⊥ BC; MB ⊥ BA;
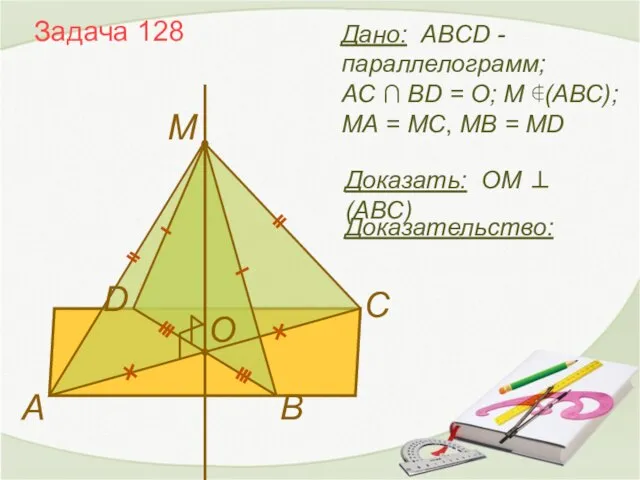
- 13. Задача 128 Доказать: OМ ⊥ (ABC) Дано: ABCD - параллелограмм; AC ∩ BD = O; М
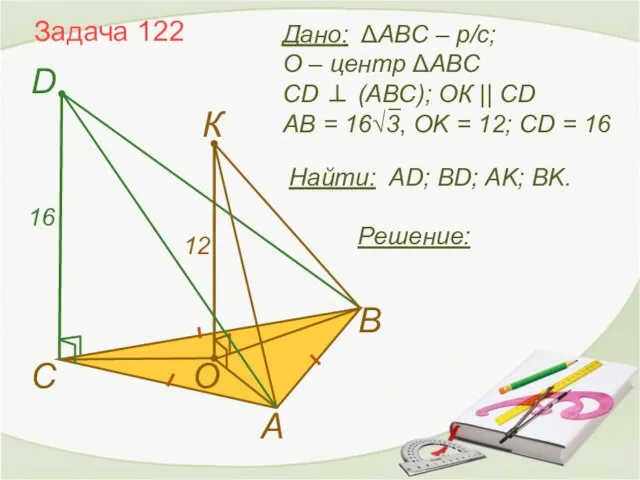
- 14. Задача 122 Найти: AD; BD; AK; BK. А В D C O К Решение: 12 16
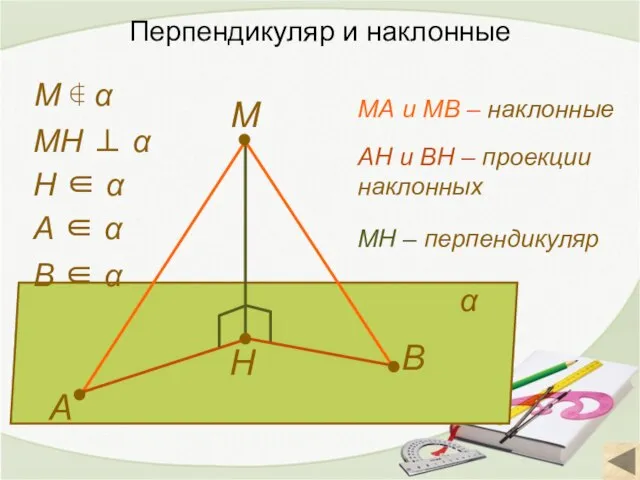
- 15. Перпендикуляр и наклонные М А В Н α МН ⊥ α А ∈ α В ∈
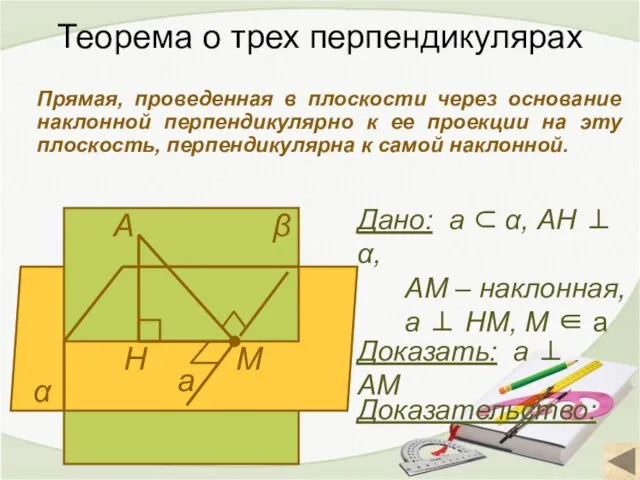
- 16. Теорема о трех перпендикулярах Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на
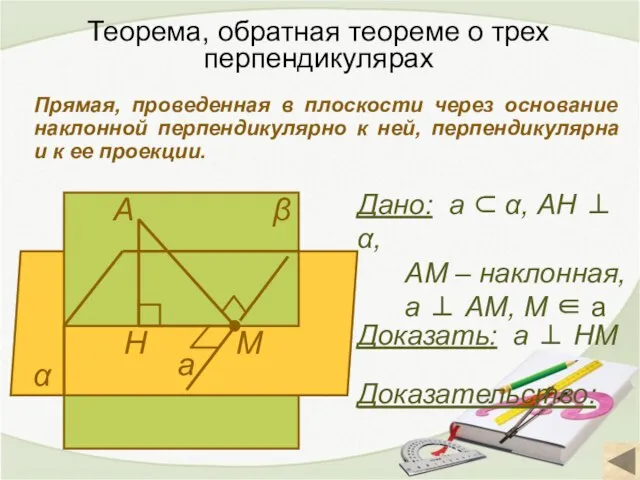
- 17. Теорема, обратная теореме о трех перпендикулярах Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
- 19. Скачать презентацию
 Урок математики в 1 классе
Урок математики в 1 классе Буквенные выражения
Буквенные выражения Дискретное преобразование Фурье (окончание)
Дискретное преобразование Фурье (окончание) Третий признак подобия треугольников
Третий признак подобия треугольников Линейная регрессия
Линейная регрессия Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Сфера и плоскость
Сфера и плоскость Уравнение. Корень уравнения
Уравнение. Корень уравнения Степень с натуральным показателем и ее свойства. Обобщение. 7 класс
Степень с натуральным показателем и ее свойства. Обобщение. 7 класс Противоположные числа. Устный счет
Противоположные числа. Устный счет Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов Теоремы синусов и косинусов. Тест
Теоремы синусов и косинусов. Тест Справочный материал. 9 класс
Справочный материал. 9 класс Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число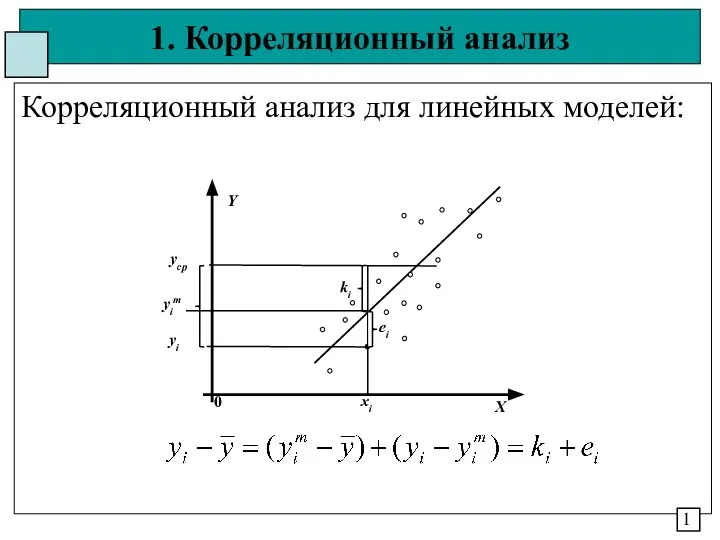 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Подготовка к ГИА по математике. Задания 6
Подготовка к ГИА по математике. Задания 6 Презентация на тему О числах
Презентация на тему О числах  Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)  Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Построение диаграмм и графиков
Построение диаграмм и графиков Тесты по математике
Тесты по математике Геометрическая прогрессия
Геометрическая прогрессия Параллелепипед и куб. 3 класс
Параллелепипед и куб. 3 класс Сумма углов треугольника
Сумма углов треугольника Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла Линии на плоскости
Линии на плоскости