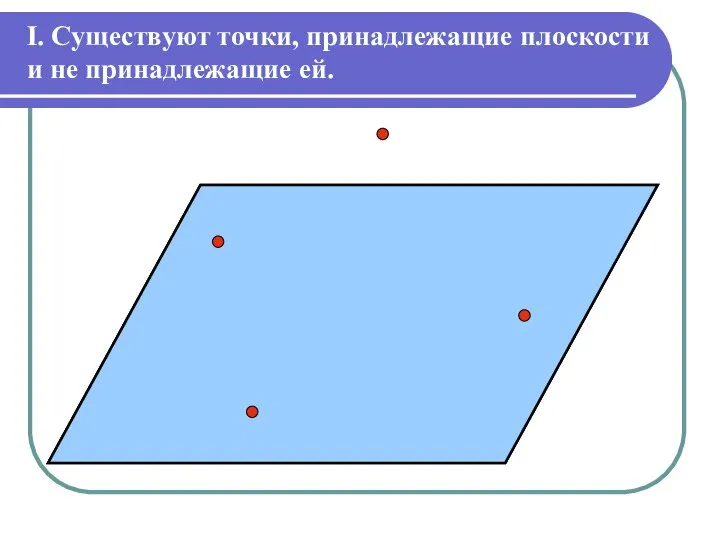
Слайд 2I. Существуют точки, принадлежащие плоскости
и не принадлежащие ей.
Слайд 3II. Если две различные точки принадлежат плоскости, то и вся прямая принадлежит
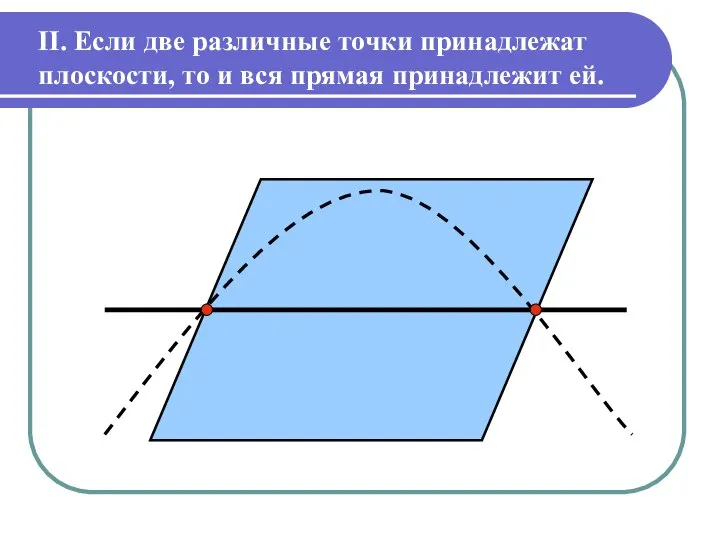
ей.
Слайд 4II. Если две различные точки принадлежат плоскости, то и вся прямая принадлежит
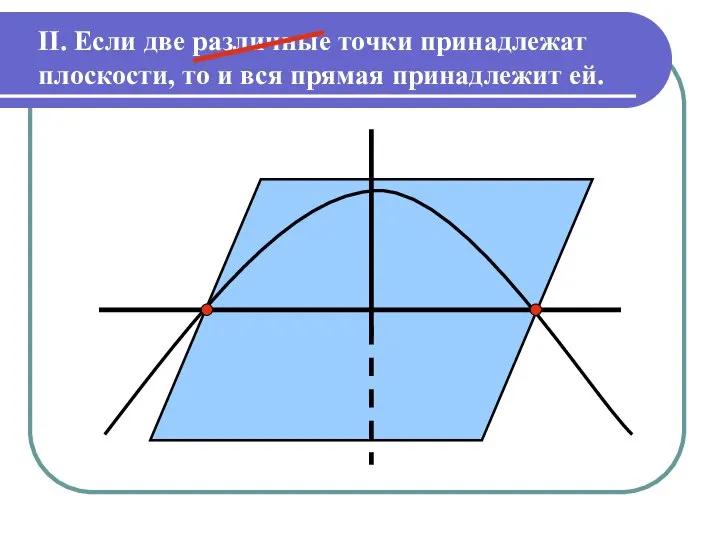
ей.
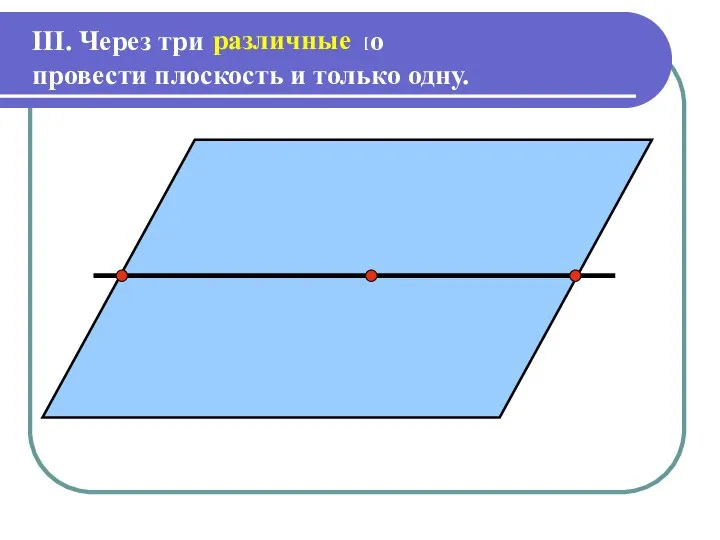
Слайд 5III. Через три
провести плоскость и только одну.
точки можно
различные
Слайд 6IV. Если две плоскости имеют одну общую точку, то они пересекаются по
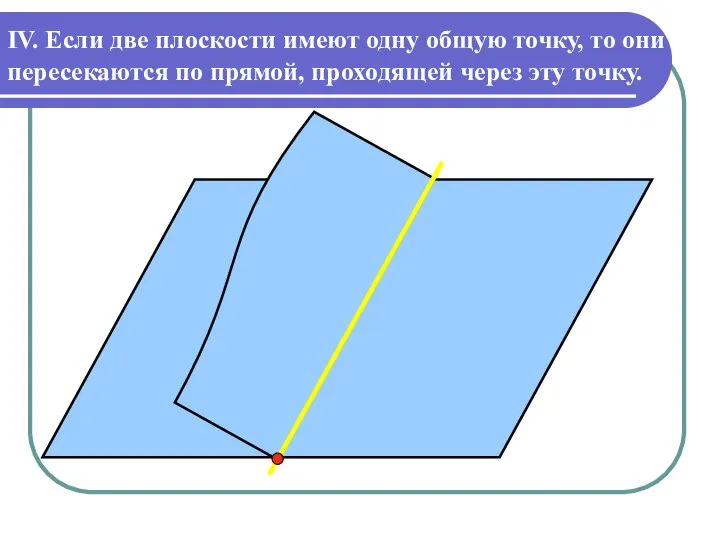
прямой, проходящей через эту точку.
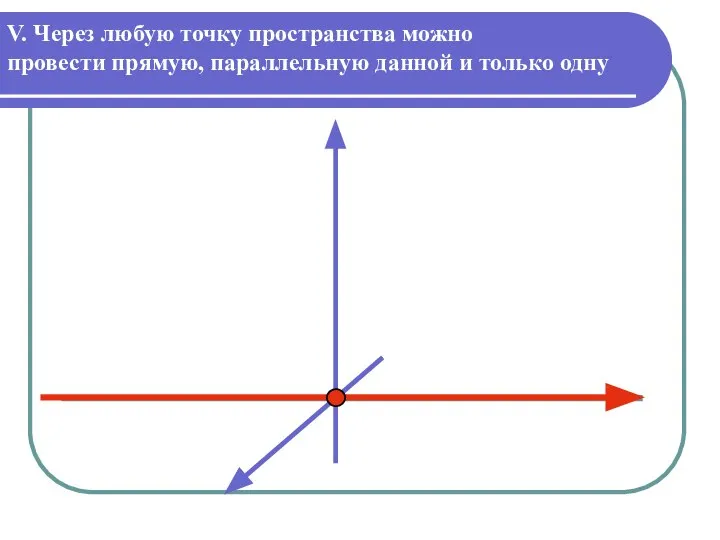
Слайд 7V. Через любую точку пространства можно
провести прямую, параллельную данной и только одну
Слайд 8V. Через любую точку пространства
провести прямую, параллельную данной и только одну
можно
вне
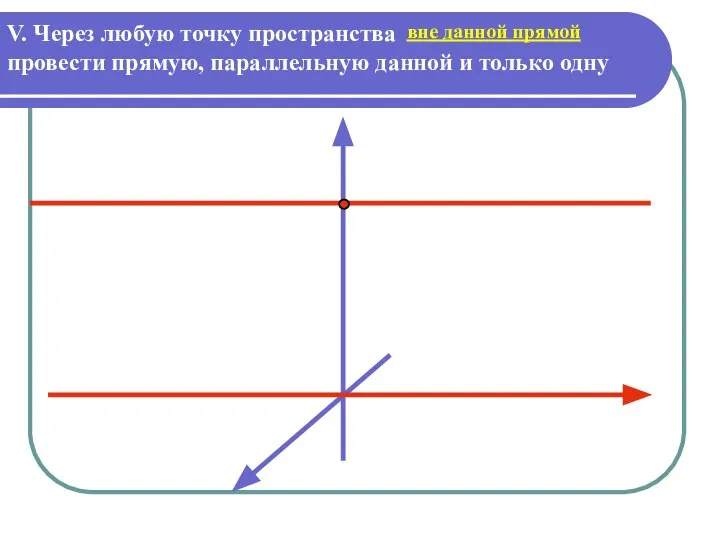
данной прямой
Слайд 9Следствия из аксиом
В этих теоремах формулируются
еще 3 способа построения плоскости
Плоскость можно провести

через:
прямую и не лежащую на ней точку
две пересекающиеся прямые
две параллельные прямые
Слайд 10Т.1 Через прямую и
провести плоскость и только одну.
точку можно
не лежащую на
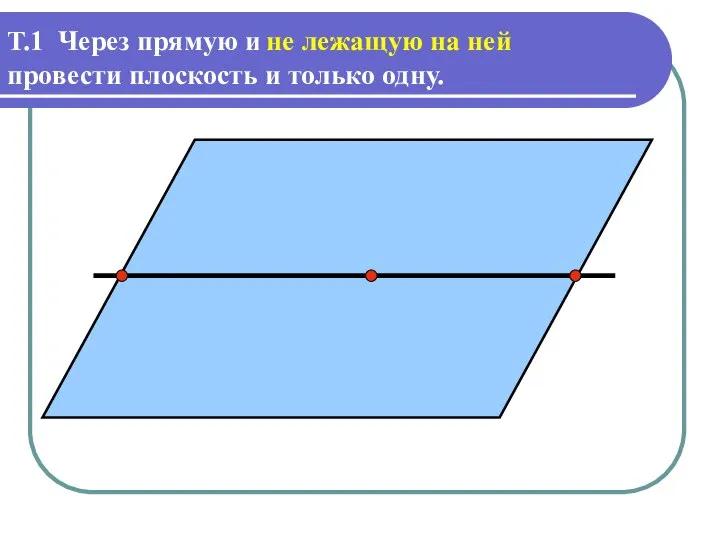
ней
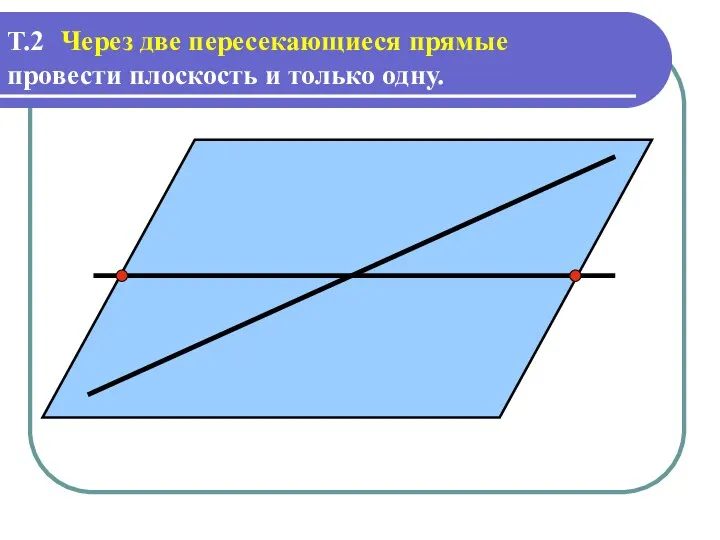
Слайд 11Т.2
провести плоскость и только одну.
можно
Через две пересекающиеся прямые










 Накопленная частота и др
Накопленная частота и др Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Симметрия в пространстве. Понятие правильного многогранника
Симметрия в пространстве. Понятие правильного многогранника Тема_5_2022
Тема_5_2022 Теоретический зачет по теме Начальные геометрические сведения
Теоретический зачет по теме Начальные геометрические сведения Квазистатическое моделирование в системе TALGAT
Квазистатическое моделирование в системе TALGAT Презентация на тему Прямоугольный параллелепипед и его свойства
Презентация на тему Прямоугольный параллелепипед и его свойства  Векторы в пространстве
Векторы в пространстве Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12
Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12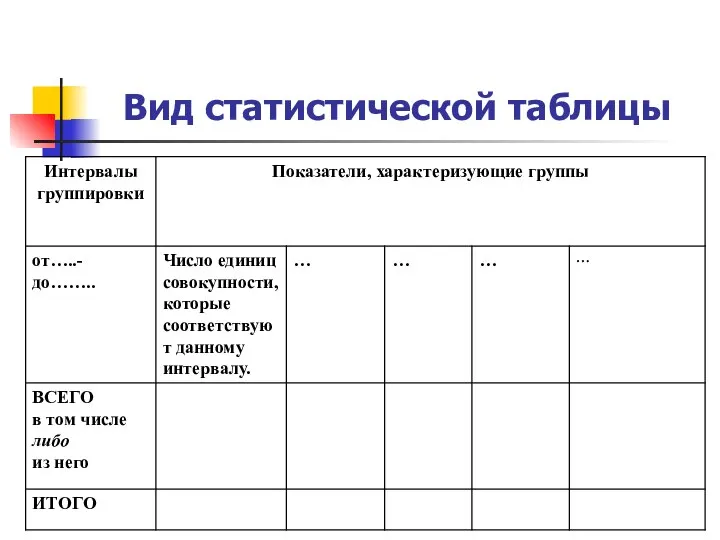 Вид статистической таблицы
Вид статистической таблицы Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей. Лекция 2
Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей. Лекция 2 Скалярное произведение векторов. 9 класс
Скалярное произведение векторов. 9 класс Решение типовой задачи
Решение типовой задачи ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел»
ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел» Восстанови ряд чисел
Восстанови ряд чисел Игра Музыкальная математика
Игра Музыкальная математика Показательное неравенство
Показательное неравенство Решение задач с помощью уравнений
Решение задач с помощью уравнений Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Геометрическая прогрессия. Формула n-го члена геометрической прогрессии Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Разряды чисел
Разряды чисел Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь Пифагор – основоположник современной геометрии
Пифагор – основоположник современной геометрии Разностные методы решения задач математической физики. Построение разностных схем интегро-интерполяционным методом
Разностные методы решения задач математической физики. Построение разностных схем интегро-интерполяционным методом Математические этюды
Математические этюды Мультиколлинеарность
Мультиколлинеарность Дифференциальные уравнения
Дифференциальные уравнения Множества и операции над ними
Множества и операции над ними