Слайд 2ПЛОСКАЯ ЛИНИЯ В R2
F(x, y)=0
Axkym
Ax+By+C=0

Слайд 3Уравнение прямой l по точке M0(x0,y0) и нормальному вектору ( ).
A(x-x0)+B(y-y0)=0

Слайд 4Уравнение прямой l по точке M0(x0,y0) и направляющему вектору ( )

Слайд 5Уравнение прямой l по двум точкам M1(x1,y1) и M2(x2,y2)

Слайд 6Уравнение прямой l по точке и угловому коэффициенту
(y-y0)=tg?(x-x0)
k= tg?
(y-y0)=k(x-x0)

Слайд 8Уравнение прямой с угловым коэффициентом
(прямая наклонена к OX под углом ?

и пересекает ось OY в точке (0; b)).
y=kx+b
1) если b=0, то уравнением примет вид y=kx. (уравнение прямой, проходящей через начало координат);
2) если k=0, то y=b (уравнение прямой, параллельной оси OX);
3) если k=b=0, то y=0 (уравнение оси OX).
Слайд 9Угол между двумя прямыми y=x+b1 и y=k2x+b2
Необходимое и достаточное условие параллельности двух

прямых:
l1||l2<=> k1= k2
Условием перпендикулярности двух прямых.
k1⋅k2 =-1=> l1⊥l2
Слайд 10ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ
Ax+By+C=0
С=0, Ax+By=0 (через начало координат)
А=0, В≠0 (параллельно оси ОХ)
А ≠

0, В=0 (параллельно оси ОУ)
А ≠ 0, В=0, С = 0 х=0 (уравнение оси ОУ)









 Площади. Тест 8 класс
Площади. Тест 8 класс Презентация на тему Знакомство с умножением
Презентация на тему Знакомство с умножением  Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей
Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей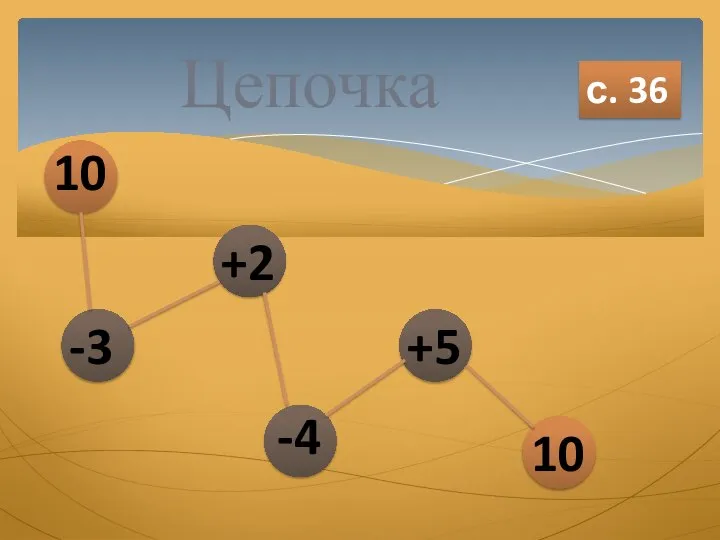 Виды весов
Виды весов Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Производная неявной функции
Производная неявной функции Равенство треугольников
Равенство треугольников Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Квадратичная функция. Подготовка к ГИА
Квадратичная функция. Подготовка к ГИА Число и цифра 2
Число и цифра 2 Основы теории вероятности и математической статистики. Лекция 4
Основы теории вероятности и математической статистики. Лекция 4 Postoroenie_gr_trigon_f
Postoroenie_gr_trigon_f Задачи на смекалку (ответы)
Задачи на смекалку (ответы) Проценты
Проценты Виды графов
Виды графов Понятие логарифма
Понятие логарифма Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Методы теории вероятностей и математической статистики в выборе фильма
Методы теории вероятностей и математической статистики в выборе фильма Высоты треугольников
Высоты треугольников Интерполирование полиномами Ньютона
Интерполирование полиномами Ньютона Занимательная математика. 1 класс
Занимательная математика. 1 класс Координаты вектора
Координаты вектора Процент. Знать и уметь находить
Процент. Знать и уметь находить Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс
Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс Решение линейных неравенств
Решение линейных неравенств Квадраты и гномоны
Квадраты и гномоны Системы логического управления ( СЛУ )
Системы логического управления ( СЛУ )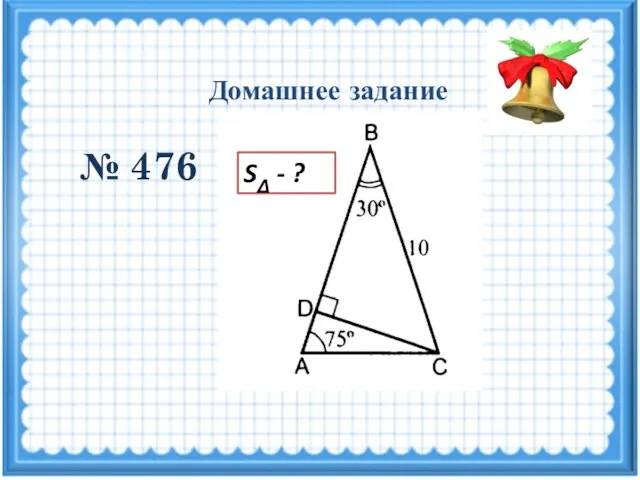 Домашнее задание № 476
Домашнее задание № 476