Содержание
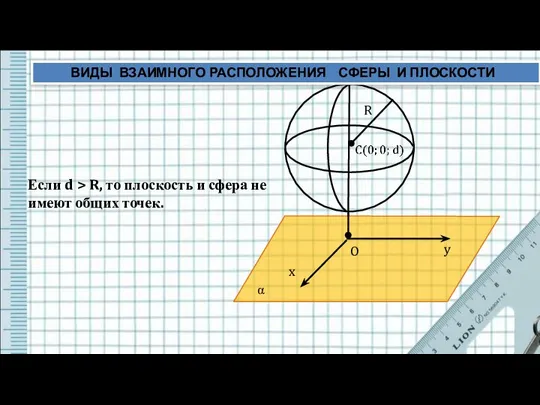
- 2. z y x O R α Если d ВИДЫ ВЗАИМНОГО РАСПОЛОЖЕНИЯ СФЕРЫ И ПЛОСКОСТИ
- 3. z y x O α R Если d > R, то плоскость и сфера не имеют
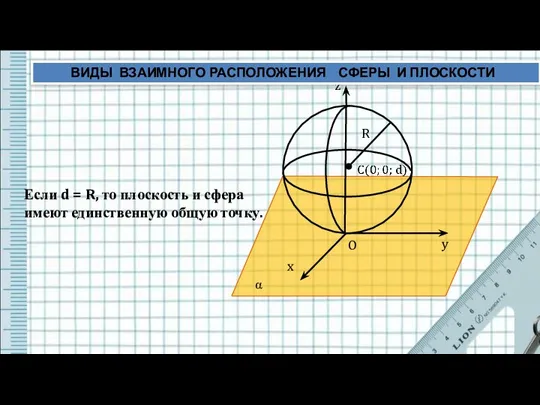
- 4. z y x O α R Если d = R, то плоскость и сфера имеют единственную
- 5. A O α – касательная плоскость к сфере А – точка касания Касательной плоскостью называется плоскость,
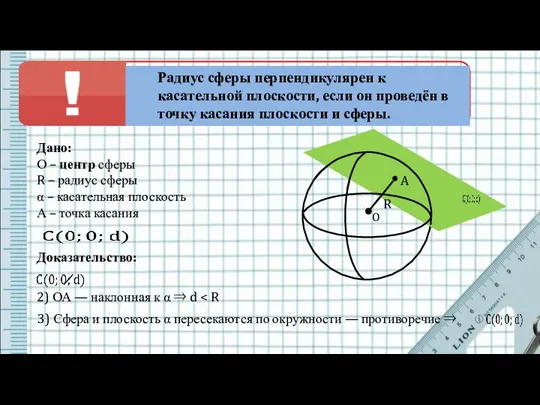
- 6. Дано: О – центр сферы R – радиус сферы α – касательная плоскость А – точка
- 7. A O R Доказательство: 2) d=R ⇒ плоскость и сфера имеют одну общую точку ⇒ ⇒
- 9. Скачать презентацию



 Линейная алгебра Матрицы
Линейная алгебра Матрицы Презентация по математике "Дроби на Руси" -
Презентация по математике "Дроби на Руси" -  Условная минимизация. Прямые методы решения задачи условной минимизации
Условная минимизация. Прямые методы решения задачи условной минимизации Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Интерактивный тренажёр В стране Математики. 1 класс
Интерактивный тренажёр В стране Математики. 1 класс Непрерывные дроби
Непрерывные дроби Частные производные. Полный дифференциал функции
Частные производные. Полный дифференциал функции Решение треугольников
Решение треугольников Статистический анализ результатов мониторинга
Статистический анализ результатов мониторинга Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Презентация на тему Прием письменного деления многозначных чисел на однозначное число
Презентация на тему Прием письменного деления многозначных чисел на однозначное число  Умножение на 5. Считаем в уме легко!
Умножение на 5. Считаем в уме легко! Задача о рюкзаке. Backpack problem
Задача о рюкзаке. Backpack problem Нахождение неопределенного интеграла
Нахождение неопределенного интеграла Пересечение геометрических фигур
Пересечение геометрических фигур Применение технологий Веб 2.0 на уроках математики
Применение технологий Веб 2.0 на уроках математики Решение иррациональных уравнений
Решение иррациональных уравнений Прохождение случайной волны через отверстие в экране. Теорема Ван-Циттерта-Цернике
Прохождение случайной волны через отверстие в экране. Теорема Ван-Циттерта-Цернике Счет до 1000
Счет до 1000 Многочлены
Многочлены Предел функции в бесконечности
Предел функции в бесконечности Powtórzenie do klasówki
Powtórzenie do klasówki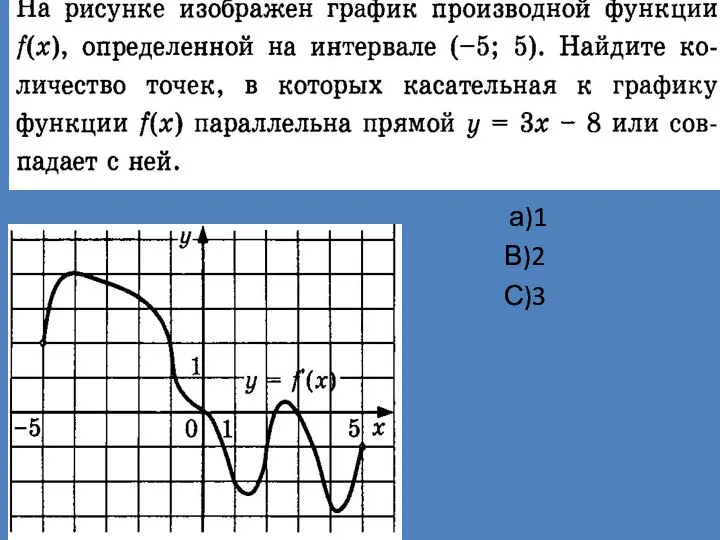 График производной функции
График производной функции Формулы и функции в Excel
Формулы и функции в Excel Opredelenny_integral
Opredelenny_integral Мнимые числа. Определение комплексных чисел
Мнимые числа. Определение комплексных чисел Основы математической статистики. Регрессионный и корреляционный анализы
Основы математической статистики. Регрессионный и корреляционный анализы ВПР по математике. Тренировочные задания
ВПР по математике. Тренировочные задания